1. 引言
燃气轮机涡轮叶片的工作环境极其严苛 [1] ,商用燃气轮机内部的工作温度通常可以达到1200℃左右,航空燃气轮机内部温度甚至可能超过1350℃,为了保证叶片能在高温下保持足够的强度和稳定性,避免因过热导致的材料性能下降甚至失效,高效的冷却系统至关重要。最常见的冷却方法是在保证强度的前提下在叶片内部设置多条冷却通道 [2] ,在通道中通入流体,冷热交换使叶片冷却。在叶片工作的过程中,冷却通道中的流体运动与叶片自身的旋转相互作用产生振动,极易使叶片变形,产生极大的危害。因此研究包含冷却通道的旋转叶片的振动特性对于合理设计燃气轮机结构具有重要意义。
早在20世纪初各个国家对叶片就展开了相关研究,在早期的研究文献中普遍将复杂的叶片结构简化为旋转悬臂梁 [3] [4] 、板 [5] 、壳 [6] 系统。上述研究都是直接研究实心结构在自身旋转下对系统振动的影响,但是都没有涉及到叶片内部冷却流体流动所带来的影响,在之后的研究 [7] [8] [9] [10] [11] 发现输流管内流体也会影响到叶片的动力学行为。Bourriéres [12] 运用经典力学对输流管结构进行振动特性分析,推导其振动微分方程,但是并没有引起广泛的注意,直到Païdoussis [13] 总结了前人的研究将输流管,研究了悬臂输流管这一种含有非保守内流效应的系统受不同参数影响的动力学特性。最常用到的提高悬臂输流管稳定性的方法是在输流管自由端处添加的集中质量 [14] [15] [16] ,在叶片结构中集中质量被称之为叶冠 [17] 。
目前旋转输流管的研究根据旋转中心轴的不同大致可以分为两类,第一类是旋转中心轴与输流管中轴线重合,如:深井石油钻柱;第二类旋转中心轴与输流管中轴线垂直,如:燃气轮机涡轮叶片。目前第二类是旋转输流管的相关研究还比较少,杨佳丽 [18] 详细总结了在旋转情况下使用铁木辛柯梁理论对输流管的振动特性分析。Yoon [19] 研究了变转速情况下输流管的力学行为变化。Zhang [20] 基于Lagrange原理和假设模态法建立了旋转输流管的动力学模型研究了在不同参数下旋转对临界流速的影响。
综上,叶片在内部流体作用下会发生在特定流速下产生颤振失稳和屈曲失稳现象。为了使理论计算模型更为接近现实叶片的结构Zhang [20] 研究了在含有双冷却通道下叶片的不同的动力学行为,但是很显然仍然不足以描述含有叶冠内部具有复杂的蛇形冷却通道的涡轮叶片结构。本文在 [20] 的基础上,建立了含有集中质量相邻冷却通道流体流动方向不同的旋转输流管动力学方程,使用能量法推导含有多条不同流动方向冷却通道的旋转输流管运动学方程,探究了在不同的系统参数组合下叶片振动特性变化规律。
2. 模型描述与动力学方程建立
本文将燃气轮机涡轮叶片简化为如图1所示的三通道旋转输流管模型,其中轮毂半径为r叶片高度为h,宽度为b,长度为L,通道的半径为ri (i = 1, 2, 3),通道与输流管中轴线的距离为di (i = 1, 2, 3),单位长度固体的质量为m,单位长度流体的质量为Mi (i = 1, 2, 3),端部集中质量为Tm,输流管的转动速度为Ω,输流管内流体任意一点相对于管道的流动速度为Ui (i = 1, 2, 3)。为了简化析过程,使用欧拉梁的基本假设:1) 在梁发生弯曲变形时,垂直于梁中性轴的任一横截面在变形后仍然保持平面,并且该平面始终与中性轴保持垂直;2) 欧拉梁理论假设梁在受到弯矩作用时,只发生弯曲变形,而不考虑剪切变形的影响。
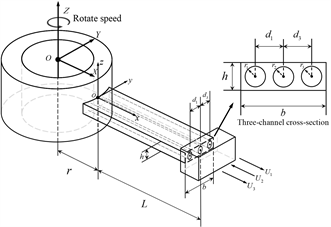
Figure 1. Rotating flow pipe with concentrated mass in multi channel flow channels
图1. 含集中质量多通道输流通道旋转输流管模型
输流管的变形势能和旋转产生的轴向伸缩势能为:
(1)
(2)
输流管和流体的动能:
(3)
(4)
非保守系统切向跟随力做功:
(5)
系统下的旋转输流管的Lagrange函数为:
(6)
(7)
将公式(6)中计算得到的Lagrange函数代入到Lagrange方程中并将其中所有的元素进行无量纲化处理,为了方便书写,省略所有无量纲量的星号*,得到如下系统矩阵形式的动力学方程。
(8)
矩阵方程中各元素的表达如:
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
求解此矩阵方程的特征值问题,计算得到含有阻尼项的前三阶特征频率。在流速不断增加的过程中,系统某阶固有频率从正值变为0时输流管出现屈曲失稳现象,此时的流速就是屈曲失稳流速;当系统某阶阻尼频率从正值变为负值时输流管出现颤振失稳现象,此时的流速就是颤振失稳流速。输流管发生屈曲失稳或者颤振失稳的最小流速,称为该输流管系统的临界流速。
为验证本文所用的方法的可行性,将含集中质量多通道输流管模型简化为单通道输流管数,文献 [14] 中自由端含集中质量单通道输流管前两阶固有频率和阻尼与本文使用方法计算的结果作比较,对比结果如表1所示,两种方法计算得到结果基本吻合。

Table 1. Comparison of the natural frequencies of cantilever fluid-conveying pipe system with an end-mass from the present study and the reference (M = 0.1, Tm = 0.3)
表1. 自由端含集中质量悬臂输流管系统固有频率本文计算值与文献对比(M = 0.1, Tm = 0.3)
3. 多通道输流管动力学特性分析
在工程实际应用背景下,理论模型采用多条流动方向不同的输流管更具备参考价值,因此将旋转叶片简化为三冷却通道的旋转输流管r1,r2,r3设置为相同大小,使输流管的截面仍然保持为中心对称结构。在固定端绝对流速为U*的情况下,使中心位置输流管流体流动方向与两侧的相反。
图2给出了不同中间管道流动方向及流速对输流管前三阶固有频率的影响(M* = 0.2, Ω* = 0)。一阶模态均会发生屈曲,在中间管道流体从自由端流向固定端的情况下,U* = 1.5二阶模态发生屈曲,三阶模态均会发生屈曲,但是三阶屈曲临界流速远小于一阶屈曲临界流速。
 (a) 1st mode
(a) 1st mode  (b) 2nd mode
(b) 2nd mode  (c) 3rd mode
(c) 3rd mode
Figure 2. The first three natural frequencies of a single channel flow tube with different flow directions vary with the flow velocity
图2. 不同中间管道流动方向及流速对三通道输流管前三阶固有频率随流体流速变化曲线
为了揭示不同方向流体流动对三通道输流管稳定性的影响,图3绘制了不同中间管道流速比下三通道输流管特征轨迹变化图,得到如下规律:
如图3(a)所示,转速对三通道流体均由固定端流向自由端输流通道特征轨迹影响较小。
如图3(b)所示,当三条管道流速比值接近1:−1.9:1时,三条轨迹曲线都在阻尼为0的附近波动,这是由于单位时间从自由端流出的流体量与固定端流出的流体量接近的时候,输流管切向跟随力所做的功会趋近于0,系统的阻尼也因此趋近于0,此时特征轨迹曲线与实轴基本重合;中间管道流速比值接近1:−0.1:1时,曲线无限接近于固定端到自由端输流通道特征轨迹影响。系统的一阶固有频率经历一个随流速比值先减小再增大再减小的过程,起初二阶颤振流速小于一阶屈曲流速,但是颤振减小速度大于屈曲减小速度,所以系统临界流速会经历一个屈曲–颤振–屈曲的过程。
 (a) U* Ratio = 1:0.1:1 to 1:1.9:1 (b) U* Ratio = 1:−0.1:1 to 1:−1.9:1
(a) U* Ratio = 1:0.1:1 to 1:1.9:1 (b) U* Ratio = 1:−0.1:1 to 1:−1.9:1
Figure 3. Trend diagram of influence of different velocity ratios on characteristic trajectories
图3. 不同流速比对特征轨迹影响趋势图
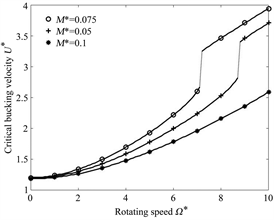
如图4,图5系统失稳流速随着转速的增加而增加,更加趋于稳定。当三条通道速度比值为1:1:1时(图4,图5(a))在单位面积流体质量较小时系统主要以二阶颤振失稳为主,在转速增加的过程中,颤振临界流速提升速度大于屈曲临界提升速度,系统的失稳方式由颤振变化为屈曲,在转速继续增加的过程中,系统会发生二三阶的模态转迁现象,当单位流体质量增加的过程中,发生转迁的转速不断增加;在单位面积流体质量较大时系统主要以屈曲失稳为主,失稳方式不再发生变化。
当三条通道速度比值为1:−1:1 (图4,图5(b))由于中间管道的影响,不发生模态转迁;第三阶频率不再持续稳定而会发生屈曲失稳,但是失稳流速小于第一阶屈曲临界流速,所以不做讨论;在单位面积流体质量较小时系统的一阶固有频率经历先减小在增加的过程,在转速增加的过程中一阶固有频率初次下降的过程中不再降为0,发生屈曲失稳的流速发生突变,系统临界失稳流速由屈曲失稳变为颤振失稳;单位面积流体质量较大时系统主要以屈曲失稳为主,屈曲失稳流速不发生突变,失稳方式不发生变化。
 (a) U* Ratio = 1:1:1 (b) U* Ratio = 1:−1:1
(a) U* Ratio = 1:1:1 (b) U* Ratio = 1:−1:1
Figure 4. Influence of rotational speed on critical buckling velocity of three-channel pipe
图4. 转速对三通道输流管屈曲临界流速影响
 (a) U* Ratio = 1:1:1 (b) U* Ratio = 1:−1:1
(a) U* Ratio = 1:1:1 (b) U* Ratio = 1:−1:1
Figure 5. Influence of rotational speed on critical flutter velocity of three-channel pipe
图5. 转速对三通道输流管颤振临界流速影响
如图6所示为不同集中质量大小对特征轨迹影响趋势图,第二阶模态则显示出随着端部质量增大,其颤振失稳现象更不容易发生,第二阶模态的临界流速随着端部质量增大而增大,这是由于端部集中质量强化了应力刚化效应,增强了结构的刚度,从而提高了整体稳定性。随着端部集中质量的改变,原本的振动模态阶数可能会发生变化,即发生模态转迁现象 [15] 。
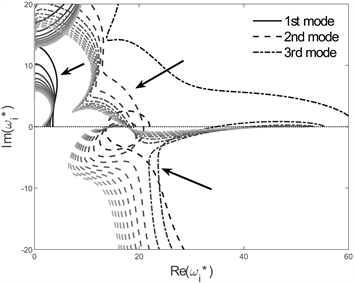
Figure 6. Trend diagram of influence of different concentration masses on characteristic trajectories
图6. 不同集中质量大小对特征轨迹影响趋势图
图7揭示了三输流管道叶片不同中间管道流动方向对前三阶复模态节点位移的影响。当流速比为1:1:1时,由于相位随时间逐渐变化,(图7(a))能观察到复模态系统三阶模态出现明显的节点位移现象,当流速比为1:−1:1时(图7(b))由于中间通道的影响,系统相位影响对模态影响较小,未能观察到明显的节点位移。这是由于复模态分析下相位是由阻尼矩阵G产生,单位时间内流出流体质量越大,相位移动越明显,中间管道与两边管道流向相反时,单位时间内流出流入流体相抵消,矩阵G影响降低,相位不再明显。
 (a) U* Ratio = 1:1:1
(a) U* Ratio = 1:1:1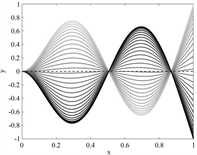
 (b) U* Ratio = 1:−1:1
(b) U* Ratio = 1:−1:1
Figure 7. The first three modal responses of the flow tube at different velocity ratios
图7. 不同流速比下输流管前三阶模态响应
图8呈现了集中质量变化对输流管前两阶模态响应中复模态节点位移的影响。当Tm = 0时,在特定模态下的在自由端纵向位移相对较大,管道更容易激发并呈现出显著的模态振动响应,其动态稳定性相对较弱。当Tm = 0.5时系统的自由端纵向位移相对较小,在同样的外部激励条件下,管道的模态响应被抑制,不易产生明显的振动。
 (a) Tm = 0
(a) Tm = 0 (b) Tm = 0.5
(b) Tm = 0.5
Figure 8. The first three modal responses of the flow tube under different concentrated masses (Ui* = 3)
图8. 不同集中质量下输流管前三阶模态响应(Ui* = 3)
4. 结论
本文将燃气轮机涡轮叶片简化为含有集中质量多通道不同流向的旋转输流管系统,分别计算管道和内部流体的动能和势能以及外力功,带入到Lagrange方程得到系统的动力学方程矩阵,计算矩阵方程的特征值求解前三阶固有频率和阻尼频率,得到内流作用和自身旋转对系统的动力学特性影响如下:
1) 当单位时间在自由端流出和流入的流体质量相同时,系统阻尼始终为0,不再发生颤振失稳。输流管内部流体流动方向和自身转动都会显著影响系统的临界流速和模态转迁。在单位面积流体质量较小时,系统临界失稳流速以颤振失稳为主,随着转速增加失稳方式会发生改变;在单位面积流体质量较大时,系统临界失稳流速以屈曲失稳为主。
2) 由于转动和集中质量使输流管在轴向产生了拉伸作用,使叶片在一定范围内具有明显的应力刚化效应,可以有效的提高系统的稳定性。
3) 单位时间内流出系统的;流体质量会影响前三阶复模态节点位移出现的速度,不同集中质量大小会显著影响输流管在自由端的纵向位移长度。

