1. 引言
高校毕业生的就业情况和发展趋向是国家、社会、家庭的关注热点,也是一项系统工程,关系到社会的稳定。高等学校作为高水平人才培养基地,义不容辞地肩负着大学生就业能力培养和就业观念教育的重任。2024年,高校毕业生人数达1179万。随着我国高等教育由“精英化”进入“大众化”时代,高校毕业生增幅逐年加大,就业问题非常突出,已经成为全社会关注的重点。
就业是民生之本,对整个社会生产和发展具有重要意义。就业能使劳动力与生产资料相结合,生产出社会所需要的物质财富和精神财富,促进社会生产的发展。就业问题关系到社会稳定。大学生的就业情况定量分析及就业形势的预测模型的研究,有利于提高就业,为社会贡献出更多的价值,从而促进全面发展。
在区域因素的条件下分析此毕业生的就业现状,首先运用层次分析法[1],建立模型指会构造判断矩阵(成对比较)矩阵,求解判断矩阵的特征向量,最后对判断矩阵的一致性进行检验,来得出区域因素对就业情况的影响。之后先运用时间序列模型[2]进行平稳性检验,确定模型的阶数,再进行参数估计与诊断检验[3],最后用建立的ARIMA模型进行预测出未来两年的整体就业情况。在最后应用最小二乘回归(PLSR)用于解决两组就业结构的相互依赖关系,并研究用一组变量去预测另一组变量来得出就业结构的未来趋势,以公式化来清晰展示,为大学生就业提供更全面的数据参考,清晰未来就业的大环境,以及在就业选择上能通过预测的趋势明确方向,进而提高就业率,增加大学生就业满意度。
2. 区域因素影响下的大学生就业情况定量分析
上海、沈阳地区本科大学生就业情况分析
层次分析法数学模型
层次分析法[2]的原理,层次分析法根据问题的性质和要达到的总目标,将问题分解为不同的组成因素,并按照因素间的相互关联影响以及隶属关系将因素按不同的层次聚集组合,形成一个多层次的分析结构模型,从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定(表1)。
Table 1. Scaling methods
表1. 标度方法
相对重要性 |
定义 |
1 |
同等重要 |
3 |
略微重要 |
5 |
相当重要 |
7 |
明显重要 |
9 |
绝对重要 |
2 4 6 8 |
两个相邻判断的中间值 |
1/3 |
略微不重要 |
1/5 |
相当不重要 |
1/7 |
明显不重要 |
1/9 |
绝对不重要 |
1/2 1/4 1/6 1/8 |
两个相邻判断的中间值 |
1) 建立层次结构模型
最高层(目标层):决策的目的、要解决的问题
中间层(准则层或指标层):考虑的因素、决策的准则
最低层(方案层):决策时的备选方案
2) 构造判断(成对比较)矩阵
判断矩阵(见表2)是表示本层所有因素针对上一层某一个因素(准则或目标)的相对重要性的比较。判断矩阵的元素
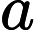

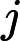 表示的是第i个因素相对于第j个因素的比较结果,这个值使用的是Santy的1~9标度方法给出[2]。
表示的是第i个因素相对于第j个因素的比较结果,这个值使用的是Santy的1~9标度方法给出[2]。
3) 求解判断矩阵的特征向量。采用方根法计算矩阵特征向量的近似值[1]
第一步:计算判断矩阵A每行元素乘积的n次方根,公式如下:
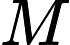


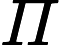
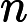
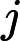


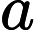





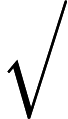
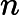
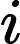
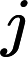
第二步:将
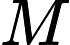
 归一化公式如下:
归一化公式如下:
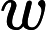


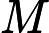
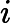

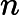
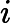

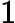
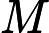
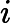
第三步:计算判断矩阵的最大特征根
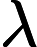


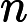



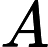
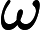

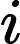
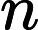
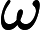

Table 2. Output results of index
表2. 指标指数的输出结果
指标 |
地理位置 |
经济发展 |
生活水平 |
就业政策 |
城市产业结构 |
市场需求 |
地理位置 |
1 |
0.5 |
0.667 |
0.667 |
0.909 |
0.769 |
经济发展 |
2 |
1 |
1.111 |
1 |
1 |
2 |
生活水平 |
1.5 |
0.9 |
1 |
1.25 |
2 |
2 |
就业政策 |
1.5 |
1 |
0.8 |
1 |
2 |
2 |
城市产业结构 |
1.1 |
1 |
0.5 |
0.5 |
1 |
0.833 |
市场需求 |
1.3 |
0.5 |
0.5 |
0.5 |
1.2 |
1 |
注:此表显示了所构建的判断矩阵。
4) 对判断矩阵的一致性进行检验
CI为度量判断矩阵偏离一致性指标,
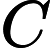
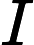

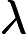

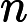
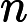

 ,CI越大判断矩阵一致性越差,CI为0时,判断矩阵具有完全一致性。CR为一致性比率,公式为:
,CI越大判断矩阵一致性越差,CI为0时,判断矩阵具有完全一致性。CR为一致性比率,公式为:
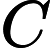


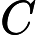
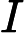

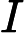 ,其中RI为平均随机一致性指标,当CR < 0.1时可以认为判断矩阵的一致性可以接受[2]。
,其中RI为平均随机一致性指标,当CR < 0.1时可以认为判断矩阵的一致性可以接受[2]。
5) 详细结论
我们可以通过层次分析法数学模型在定量分析角度上能够判断出各衡量的区位因素与就业情况之间的相对重要程度,并清晰的看到不同的区位因素对于就业情况的权重占比不同见表3。能够得到在地理位置,经济发展,生活水平等区域因素作为指标时,通过Santy的标度方法构建的判断矩阵,根据层次分析法依次得到以下结果:
Table 3. AHP hierarchical analysis results
表3. AHP层次分析结果
AHP层次分析结果 |
项 |
特征向量 |
权重值(%) |
最大特征根 |
CI值 |
地理位置 |
0.704 |
11.731 |
6.103 |
0.021 |
经济发展 |
1.244 |
20.735 |
生活水平 |
1.314 |
21.901 |
就业政策 |
1.24 |
20.665 |
城市产业结构 |
0.766 |
12.769 |
市场需求 |
0.732 |
12.199 |
注:此表展示了层次分析法的权重计算结果,根据结果对各个指标的权重进行分析。
据层次分析法可以看到不同因素对就业情况影响的比重,清晰地得到城市的生活水平是最重要的影响因素,最能影响就业选择。其次是经济发展以及就业政策对就业情况有较大的影响“见表3”。
通过层次分析法可以验证区域因素影响就业情况的权重方法是合理的“见表4”,因此不需要修改判断矩阵。
Table 4. Consistency test results
表4. 一致性检验结果
一致性检验结果 |
最大特征根 |
CI值 |
RI值 |
CR值 |
一致性检验结果 |
6.103 |
0.021 |
1.25 |
0.016 |
通过 |
注:层次分析法的计算结果显示,最大特征根为6.103,根据RI表查到对应的RI值为1.25,因此
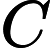


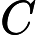
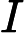

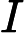

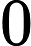
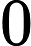

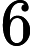

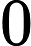
 ,通过一次性检验[4]。
,通过一次性检验[4]。
3. 就业形势的预测模型的研究
3.1. 时间序列分析
3.1.1. 模型理论
ARIMA模型[2]是被广泛运用于对各类时间序列数据分析和建模的方法。模型基于如下的观念:要预测的时间序列是由某个随机过程生成的。如果生成序列的随机过程不随时间变化,则该随机过程的结构可以被确切地刻画和描述。利用序列过去的观察值,可以外推出序列的未来值。在ARIMA模型中,序列的未来值被表示成滞后项和随机干扰项的当期及滞后期的线性函数,即模型的一般形式如下式所示:
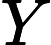


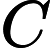

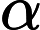

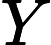





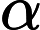
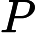
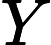


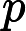

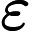


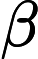

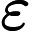





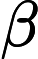
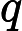
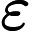


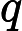
ARIMA模型的建模过程可以分为以下四个步骤[2]:
步骤1:时间序列的平稳性检验。通常采用ADF或PP检验方法,对原始序列进行单位根检验。如果序列不满足平稳性条件,可以通过差分变换或者对数差分变换,将非平稳时间序列转化为平稳时间序列,然后对平稳时间序列构建ARIMA模型。
步骤2:确定模型的阶数。通过借助一些能够描述序列特征的统计量,如自相关(AC)系数和偏自相关(PAC)系数,初步识别模型的可能形式,然后根据AIC等定阶准则,从可供选择的模型中选择一个最佳模型。
步骤3:参数估计与诊断检验。包括检验模型参数的显著性,模型本身的有效性以及检验残差序列是否为白噪声序列。如果模型通过检验,则模型设定基本正确。否则,必须重新确定模型的形式,并诊断检验,直至得到设定正确的模型形式。
步骤4:用建立的ARIMA模型进行预测。
3.1.2. 数据应用模型
该序列检验的结果显示,基于变量就业人数:
在差分为0阶时,显著性P值为0.039**,水平上呈现显著性,拒绝原假设,该序列为平稳的时间序列“见表5”。
在差分为1阶时,显著性P值为0.000***,水平上呈现显著性,拒绝原假设,该序列为平稳的时间序列“见表5”。
Table 5. ADF test list
表5. ADF检验表
ADF检验表 |
变量 |
差分阶数 |
t |
P |
AIC |
临界值 |
1% |
5% |
10% |
就业人数 |
0 |
−2.957 |
0.039** |
−14.098 |
−7.355 |
−4.474 |
−3.127 |
1 |
−8.053 |
0.000*** |
−14.155 |
−10.417 |
−5.778 |
−3.392 |
注:***、**、*分别代表1%、5%、10%的显著性水平。
系统基于AIC信息准则自动寻找最优参数,模型结果为ARIMA模型(0, 0, 1)检验表,基于变量:就业人数,从Q统计量结果分析“见表6”可以得到:数据低于6条无法进行白噪声检验[4]。
Table 6. Model parameters table
表6. 模型参数表
ARIMA模型(0, 0, 1)检验表 |
项 |
符号 |
值 |
|
Df Residuals |
3 |
样本数量 |
N |
5 |
Q统计量 |
Q6 (P值) |
-(-) |
信息准则 |
AIC |
−16.791 |
BIC |
−17.963 |
拟合优度 |
R2 |
0.334 |
注:***、**、*分别代表1%、5%、10%的显著性水平。
基于变量就业人数,系统基于AIC信息准则自动寻找最优参数,模型结果为ARIMA模型(0, 0, 1)检验表(表7),模型公式如下[4]:
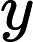
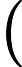
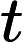


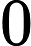
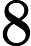
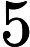
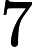

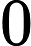
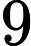
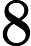
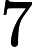

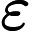
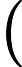
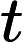



Table 7. Model test table
表7. 模型检验表
模型参数表 |
|
系数 |
标准差 |
t |
P > |t| |
0.025 |
0.975 |
常数 |
857 |
0.008 |
10.12.117 |
0 |
0.842 |
0.872 |
ma.L1 |
−0.987 |
34.63 |
−0.028 |
0.977 |
−68.861 |
66.887 |
sigma2 |
0 |
0.015 |
0.029 |
0.977 |
−0.029 |
0.03 |
注:***、**、*分别代表1%、5%、10%的显著性水平。
通过此模型的建模以及数据代入模型的研究,在数据的基础上依托模型能够在合理的基础上预测到后几年的就业率的大致趋势。在进行模型预测的时候,首先从整体出发,为了清楚每一年都就业率形势,收集了学校官方的就业率数据,之后将整理好的数据应用于时间序列模型。建模分析时在就业人数变量的基础上,得到了就业预测的模型公式。预测了2年后的就业率的数据“见表8”。可以通过预测数据与实际数据比较发现就业率整体是有减小的趋势,但预测的两年数据整体是向上增长的趋势,所以综合来看就业率还算处在一个波动较小的状态。
Table 8. Time series forecast table
表8. 时间序列预测表
预测值 |
阶数(时间) |
预测结果 |
1 |
0.843792019733489 |
2 |
0.8574496227430509 |
注:上表显示了时间序列模型最近2期数据预测情况。
3.2. 偏最小二乘回归(PLSR)模型预测就业结构占比
模型理论
最小二乘回归(PLSR) [3]是一种多因变量对多自变量的回归建模方法,是最小二乘方法的推广。用于解决两组多重相关变量间的相互依赖关系,并研究用一组变量(自变量或预测变量)去预测另一组变量(因变量或响应变量)。
当两组变量的个数很多,且线性相关,而观测数据的数量又较少时,适合用偏最小二乘回归建立的模型。
偏最小二乘回归分析在建模过程中集中了主成分分析,典型相关分析和线性回归分析方法的特点,因此在分析结果中,除了可以提供一个更为合理的回归模型外,还可以同时完成一些类似于主成分分析和典型相关分析的研究内容,提供更丰富、深入的一些信息。
对于P个因变量
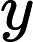

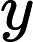
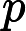 与m个自变量
与m个自变量
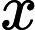

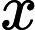
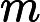 的回归问题。首先在自变量集中提出第一成分U1 (U1是
的回归问题。首先在自变量集中提出第一成分U1 (U1是
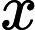

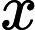
 的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分ν1,并要求U1与ν1相关程度达到最大。然后建立因变量
的线性组合,且尽可能多地提取原自变量集中的变异信息);同时在因变量集中也提取第一成分ν1,并要求U1与ν1相关程度达到最大。然后建立因变量
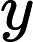

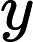
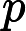 与U1的回归,重复这个过程直到提取到足够的指定的成分[3] (表11)。
与U1的回归,重复这个过程直到提取到足够的指定的成分[3] (表11)。
分析步骤
1) 通过方差解释情况(表9)和VIP (累积投影重要性) (表10)参考最大主成分数量。
2) 通过成分矩阵表(表11)得到主成分的组成情况。
3) 通过因子载荷系数表(表12)得到变量的重要性。
4) 最终得到偏最小二乘回归(PLSR)的标准化公式。
前面通过时间序列模型进行了就业形势的预测,后面深入调查就业数据,将就业数据细分到不用的就业方向上(表13)。如:是继续升学深造还是签订就业合同打算就业,从这种细分的就业结构的预测可以更加主要预测出未来的就业的主要趋势是选择升学的人更多还是选择就业的更多,也同时反映了当下社会毕业生对于就业的一个选择。在将深入调查的就业数据应用于数学模型的预测之后,可以清晰地得出两种就业选择的一个相互关系,以及可以通过其中一个判断出另外一个的就业数据,同时得出一个模型标准化的公式,通过这个公式可以推断出未来的这两种就业选择的关系。
Table 9. Explanation of factor variance
表9. 因子方差解释情况表
潜在因子 |
X方差 |
累计的X方差 |
Y方差 |
累计的Y方差(R2) |
调整后的R2 |
1 |
0.961 |
0.961 |
0.593 |
0.593 |
0.39 |
2 |
0.039 |
1 |
0.246 |
0.839 |
0.516 |
注:因子对方差解释情况表的结果显示,前1个潜在因子就可解释自变量80%的信息,前2个潜在因子就可解释自变量80%的信息[4]。
Table 10. Summary table of independent variable VIP (cumulative projected importance)
表10. 自变量VIP (累积投影重要性)汇总表
变量 |
因子1 |
因子2 |
签就业协议合同形式就业 |
1.028 |
1.012 |
升学 |
0.972 |
0.988 |
Table 11. Component matrix
表11. 成分矩阵
变量 |
因子1 |
因子2 |
签就业协议合同形式就业 |
0.727 |
0.707 |
升学 |
−0.687 |
0.708 |
年份 |
−0.812 |
0.067 |
就业率 |
0.616 |
0.117 |
本科毕业人数 |
−0.301 |
0.302 |
Table 12. Factor load coefficients
表12. 因子载荷系数
变量 |
因子1 |
因子2 |
签就业协议合同形式就业 |
0.708 |
0.687 |
升学 |
−0.707 |
0.727 |
年份 |
−0.71 |
0.137 |
就业率 |
0.643 |
1.499 |
本科毕业人数 |
−0.091 |
2.701 |
Table 13. Model coefficient results
表13. 模型系数结果
|
年份 |
就业率 |
本科毕业人数(万) |
常数 |
2021 |
0.877 |
0.3809 |
签就业协议合同形式就业 |
−0.905 |
0.021 |
0.0241798 |
升学 |
1.263 |
0.008 |
0.0259324 |
注:模型的标准化公式为:年份 = 2021.0 − 0.905*签就业协议合同形式就业 + 1.263*升学[4]。
本篇论文在具体的研究创新性方面综合有以下几点:
1) 顺应数据时代趋势,通过综合研究区域因素,分析大学生就业大数据,对就业形势进行预测,能更好地帮助大学生清晰就业趋势,明白就业现状,完成高质量就业。
2) 使用结合多种数学模型,通过多模型的一起研究,为研究能提供更有效的支持与保证。
3) 本研究对于具体的数据采用多层次的研究,从不同模型进行不同研究,从而可以让模型预测变得多因素化。
但是综合以上的研究方法仍存在局限性,首先在数据选择上由于就业数据的官方性导致就业数据不完整,从而应用于数学模型时会对模型预测有影响,其次几个数学模型之间都是独立研究,几者进行的联系不紧密,导致结论之间比较独立,没有在前模型预测的结论上再精确得出结论。
本篇论文通过三个模型研究可以为以后的毕业生就业趋势以及就业数据等进行估测,帮助更多的大学生了解目前趋势以及明白就业形式。综合以上的研究内容,可以了解到:
1) 首先在区位因素的影响下,通过层次分析法[2]的数学模型建立,不同的区位因素会对就业情况产生不同的影响。并且在具体的因素影响下模型研究出各自因素影响的比例不同。
2) 基于对就业数据的收取,利用时间序列模型[3]可以预测出在未来俩年的一个就业率,从而得出就业的一个大形势是一个相比较平稳的一个状态,但是相较于现在的就业率,预测的就业率是呈一个下滑的趋势,所以说在未来的就业率会在比较的平稳的基础上会有些减少的,这对未来的大学生就业可以成为一个提示。
3) 最后,在对就业选择结构的具体的研究下,从偏最小二乘法[3]研究下得到了相应的公式,可以判断出两种不同的就业选择之间的一个数学关系,也可以在未来通过公式的推断能够预判就业选择的发展,为更多的学生提供帮助。
最后,在未来的研究方向上首先要做的就是继续将数据结构优化,可以选择多层次,多方面,多内容的就业数据,保证就业数据的一个多元化,来为研究的准确性提出一个最基础的条件,同时,我们可以将数学模型之间建立起联系,不再是独立的研究,形成一个具体的就业研究的体系,最后,我们甚至可以通过就业体系的研究,为学生提供具体就业岗位的选择以及就业岗位咨询。
基金项目
项目支持:沈阳航空航天大学2023年大学生创新创业项目,编号Z202310143058。