1. 前言
1.1. 研究背景
草原作为地球上分布最广的陆地植被类型,分成温带草原、高寒草原等多种类型,是陆地最重要的生态系统之一。草原素有孕育生命、沉淀历史的绿色花园之称,它不仅是数以万计的江河发源地和水源涵养地,孕育着众多湖泊和冰川,还拥有着人类所需的水库、钱库和碳库等功能。林草兴则生态兴,草原对于一个国家的生态发展具有基础性和战略性作用,它有着生物多样性保育、营养元素循环、碳固持、调节气候及防水土流失等重要功能。作为世界上草原资源和种类最丰富的国度之一,中国的草原总面积约4亿公顷,占国土总面积的41%,主要分布在完达山到青藏高原东麓的西北地区。
然而随着过度放牧等人为因素,我国的天然草原开始出现不同程度的土地退化和沙漠化,植物群落类型和土壤特性等发生变化,地上、地下生物量大幅度减少,极大地影响了整个生态系统的发展。解决草原生态环境问题迫在眉睫,为此2003年党中央、国务院颁发“退牧还草”决策,目的是加强草原保护与建设。十几年的显著成果可以看出这一重大措施使得草原逐渐从衰败走向复苏,草原植被开始恢复,草原环境得到改善,同时畜牧业也实现了可持续发展,保障了牧民的长远生计。
“放牧还草”并不意味着完全禁止放牧,通常需要因地制宜地去考虑放牧方式和放牧强度,以草定畜、严格控制载畜率等。除了部分地区禁牧以外,大部分草原区域实施选择划区放牧和生长季放牧等轮回制放牧法,高效利用天然草原,达到草畜平衡,实现了草原资源的可持续利用,建立起草原和畜牧业的共生平衡生态系统。适当放牧不仅可以改善土壤质量、提高生物多样性,还能保持草场相对稳定的生产率 [1] 。
1.2. 研究目的及意义
基于上述的研究背景,本文主要以草原土地性质和可持续发展为研究对象,通过对土壤湿度等土壤化学相关元素的数据建立多种数学模型,从而去预测不同深度及不同放牧强度下土壤化学元素的分布情况;因此我们可以更加方便了解草原土地状态的性质,为后续寻找最佳放牧政策提供良好的数据基础。
此外,为呼吁国家的“加强草原保护和建设”的重要决策,达到草原资源的可持续性发展,本文建立不同放牧强度下土壤板结化程度和沙漠化指数的数学模型,希望通过该定性数学模型,寻找到最佳的放牧策略,例如放羊数量等。从而建立草原和畜牧业的和谐生态系统,保证在草原可持续发展情况下实现经济效益最大化 [2] 。
2. 模型假设
假设1:所有数据均真实可靠;
假设2:在不同放牧强度下,样本小区的土壤湿度一致;
假设3:除了提供的相关数据,无其余变量对锡林郭勒草原可持续发展产生影响。
3. 符号说明
文中符号说明如表1。
注:其他符号在文中说明。
4. 问题一:模型的建立和求解
4.1. 问题一分析
问题1主要建立不同放牧策略下内蒙古锡林郭勒草原土壤湿度和植被生物数量的数学模型。现拟从以下三个步骤去处理问题一:
(1) 首先找出影响土地湿度和植被生物数量的主要特征变量。
(2) 分析各个变量之间的自相关性和对土壤湿度和植被生物数量的影响,采用皮尔逊相关分析对收集到的变量进行特征筛选,在不同的放牧强度下选择出对土壤湿度和植被生物数量具有显著影响的变量。
(3) 分别建立四种放牧强度下土壤湿度和植被生物数量的LSTM时间预测模型。
4.2. 数据预处理
经过查阅相关文献 [3] [4] ,本文归纳总结出草原土壤湿度和植被生物数量的主要影响因素,其中影响土壤湿度和植被生物数量的主要为降水、植物干重等约30多个变量因子。同时根据放牧与植物生长之间关系和土壤含水量–降水量–地表蒸发模型的两个简单模型,也在数据支撑验证下确定这些因素对土壤湿度和植被生物数量是存在一定影响关系。
基于问题一及所给数据,可以将所提及的放牧策略主要归结为放牧强度的不同,因此针对四种放牧强度(对照、轻度放牧强度、中度放牧强度和重度放牧强度)分别组建不同放牧强度下各个变量因子对土壤湿度和植被生物数量的影响模型。
为保证数据的有效性,本文首先进行初步统计特征分析并对所用数据进行预处理。数据的预处理主要分为以下三个板块:(1) 删除缺失率较高和含零值较高的变量;(2) 基于KNN算法对缺失率较少的变量进行数值插补;(3) 拉格朗日插值法。
4.3. 特征选择——皮尔逊Pearson相关系数
为减少变量数量、提高模型效率,使得模型泛华能力更强,避免过拟合,通常在数据预处理完以后会对变量进行特征选择,其原则是尽可能获取小的、稳定的、适应性强的特征子集,同时不显著降低分类精度、不显著影响分类分布。因此可以通过特征选择找到对土壤湿度和植被生物数量最具显著影响的变量,常用的降维方法为皮尔逊Pearson相关系数,其原理为:
英国数学家Karl Pearson提出了Pearson相关系数的统计指标,并将其广泛应用于变量间的线性相关程度定量分析。Pearson相关系数的计算方式是将协方差除以两个变量的标准差,从而消除掉两个变量的量纲影响。计算公式为:
该统计指标反映了两变量之间的线性相关程度,其值介于−1和1之间。相关系数的绝对值越大,两者线性关系越强,相关系数越趋近于1或−1,相关度越强,相关系数越趋近于0,相关度越弱。当一个变量增大,另一个变量也随之增加时,说明为正相关,相关系数大于0,相反如果减小,则为负相关,相关系数小于0。如果相关系数等于0,则不存在线性相关关系。因此可以通过该方法来选择与土壤湿度相关性较强的特征变量。
由于问题一探讨的是不同放牧策略对土壤湿度和植被生物数量的影响,因此分为土壤湿度和植被生物数量两大部分去进行特征选择:
4.3.1. 土壤湿度
查阅附件资料可以得出不同放牧强度下SOC土壤有机碳及鲜重等影响因子是不同的,但一些基本变量,例平均气温等因子是固定不变的,因此在做土壤湿度的特征选择时会分成两部分对特征变量做Pearson相关分析:
(1) 基本气候变量:首先对基本气候变量做Pearson相关分析,得到了基本气候变量与土壤湿度的相关系数,如表2所示:

Table 2. Correlation coefficient table of climate variables
表2. 气候变量相关系数表
结合相关系数表2可知,相关系数大于0.4的变量与土壤湿度具有一定程度的相关性,因此结合气候变量与土壤湿度的相关系数图可以推断:最低气温极值、降水量等9个变量对土壤湿度具有一定影响,但是由于降水量、单日最大降水量和降水天数两两之间的相关系数高达80%,相关性较高,为避免变量间的耦合性带来的干扰,且降水量更能表现降水的特征,因此这三个降水相关的变量仅选择降水量,其余删除。
同理对剩余变量进行筛选,最终得出对土壤湿度有一定影响的基本气候变量为降水量、平均露点温度、平均最大持续风速共三个,如表3所示:

Table 3. Table of main climate variables
表3. 主要气候变量表
(2) 土壤、植被相关变量:
由于这类变量随着放牧强度的不同而变化,因此在进行特征选择时分成四个不同放牧强度(对照、轻度放牧强度、中度放牧强度和重度放牧强度),表4为不同放牧强度下土壤、植被相关数据与湿度的相关系数表:

Table 4. Soil and vegetation correlation coefficient table
表4. 土壤、植被相关系数表
首先在表4里选取相关系数大于0.4的特征变量,分别得到不同放牧强度下土壤湿度的影响因素。其中在重度放牧强度的情况下,STC土壤全碳与土壤湿度的相关系数达到0.49,但与SOC土壤有机碳、全氮N、土壤C/N比和SOC土壤无机碳的相关性过高,同样为避免变量间自相关性过强带来的干扰,因此选择可以删掉。
至此,整理出不同放牧强度下选择后的变量与土壤湿度的相关系数图,如图1所示:

Figure 1. Soil moisture correlation coefficient diagram (corresponding from left to right and top to bottom, four grazing intensities: control, light grazing, moderate grazing and heavy grazing)
图1. 土壤湿度相关系数图(从左到右从上到下分别对应对照、轻度放牧、中度放牧和重度放牧这四种放牧强度)
综合上述,最终得到了不同放牧强度下影响土壤湿度的不同特征变量,得到图2:
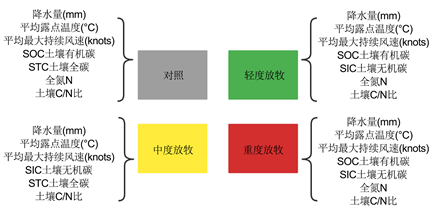
Figure 2. Characteristic variable diagram of soil moisture
图2. 土壤湿度的特征变量图
4.3.2. 植被生物数量
与土壤湿度模型不同,叶面积对植被生物数量可能存在一定的影响,因此在前面所有特征变量的基础上,本文在对植被生物数量模型进行特征选择时,增加了叶面积指数这一特征变量。对影响植被生物数量的三十多个特征变量做Pearson相关分析,得到与植被干重的相关系数表5(以轻度放牧强度为例):

Table 5. Vegetation dry weight correlation coefficient table
表5. 植被干重相关系数表
与土壤湿度模型的特征选择同理,结合表5选择相关系数大于0.4的变量,且在变量间相关性过高的变量中仅保留最能体现这一特征的变量,经过筛选后得到不同放牧强度下的显著影响因子对植被干重的相关系数如图3。
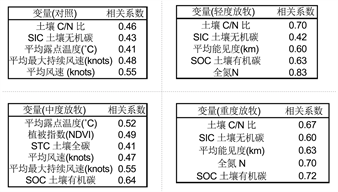
Figure 3. Correlation coefficient diagram of the number of vegetation organisms (corresponding from left to right and top to bottom, Four grazing intensities: control, light grazing, moderate grazing and heavy grazing)
图3. 植被生物数量相关系数图(从左到右从上到下分别对应对照、轻度放牧、中度放牧和重度放牧这四种放牧强度)
至此,得到了不同放牧强度下影响植被生物数量的特征变量(图4):
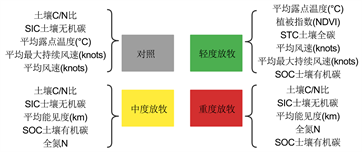
Figure 4. Characteristic variable diagram of the number of vegetation organisms
图4. 植被生物数量的特征变量图
4.4. 基于LSTM时序预测模型的建立
4.4.1. LSTM模型的原理
1997年德国计算机科学家Sepp Hochreiter和Schmidhuber首次提出长短时间记忆(LSTM)模型,是一种时间循环神经网络,为解决RNN的长序列训练过程中梯度消失问题演进而来的,能够处理具有长期依赖关系的时间序列数据,并进行准确的预测。在实际应用中,LSTM模型已经被广泛应用于各种时序预测任务 [5] ,如股票价格预测、交通流量预测、能源消耗预测等。LSTM引进三个门来保护和控制细胞状态:遗忘门 + 输入门 + 输出门,通过这三个精心设计的门来新增或删除信息。
首先,遗忘门决定当前状态应该保留或丢弃多少上一时刻的信息。将先前时刻和当前时刻输入的信息同时输入到sigmoid函数,得到的输出值在0~1之间,越靠近0表示越应该遗弃,越接近1表明越应该保留。计算公式为:
其中W,b分别为权重和偏置,
为sigmoid函数,表示每个部分有多少量可以通过。其次,输入门过滤新信息,确定什么样的新信息需要输入到细胞状态里。同样将先前状态和当前状态的信息输入进sigmoid函数里,调整输出值来确定哪些信息应该更新,0代表不重要,1代表重要。同时将值输入到tanh函数,将数值压缩至−1到1之间,最后将sigmoid输出值和tanh输出值进行相乘,决定哪些信息是重要的、需要保留的。计算公式为:
旧细胞通过遗忘门,待用信息通过输入门,两者相结合得到的结构来更新细胞状态。最后,输出门做出决策,确定当前时刻输出什么样的记忆信息,能够决定下一个状态(即隐藏状态)的值。前面两个门确定了隐藏状态需要携带的信息并当前输出,将新的单元状态和隐藏状态传递给下个时间步。计算公式为:
决定要输入的部分,结合tanh将细胞状态变换后相乘,输出结果信息。
LSTM建立预测模型主要有以下几步:(1) 数据预处理:选取数据样本,进行数据标准化处理,对数据进行归一化处理有利于训练模型的损失(loss)迭代。将数据划分成训练集和测试集。(2) 预测模型:建立预测模型需要提前确定输入层、输出层的节点数和隐藏层的神经元等模型参数,将训练样本输入到模型中,进行深度学习和数据挖掘,训练得到预测模型。(3) 评价模型:为保证预测结果的准确性和预测误差波动的稳定性,需要对模型的预测值和真实值的拟合程度进行评价,通常采用平均绝对误差(MAE)等进行评估,误差越小,说明两者之间的离散程度越小,预测结果更可靠 [6] 。
4.4.2. 土壤湿度的模型建立
在进行数据预处理和特征选择两步的处理后得到了土壤湿度的影响变量数据,分别将这些数据划分成训练集和测试集(其中80%为训练集,20%为测试集),训练集的数据用于模型的学习训练,测试集的数据用于检验模型的准确性。
本文基于Python软件,求解出不同放牧强度对土壤湿度的LSTM预测模型,共四个。不同放牧强度下20%测试样本的测试结果如图5所示,可以看出LSTM模型预测的整体效果比较好,预测值和真实值的整体走向趋势一致,拟合程度较高。

Figure 5. Measured values and true values of soil moisture (from left to right, top to bottom Corresponding to the four grazing intensities of control, light grazing, moderate grazing and heavy grazing respectively)
图5. 土壤湿度的测值与真实值(从左到右从上到下分别对应对照、轻度放牧、中度放牧和重度放牧这四种放牧强度)
4.4.3. 土壤湿度的模型评价
为了更加准确地对模型性能进行客观评价,我们需要对模型的预测值和真实值的拟合程度进行评价,本次问题选取了常见的平均绝对误差(MAE)和均方根误差(RMSE)两个指标从不同的角度对预测模型进行判断,其有着简单易懂、可靠等优点。MAE和RMSE的公式如下:
对建立好的LSTM模型计算不同放牧强度下的MAE、RMSE误差值,通常情况下MAE、RMSE误差值越小,预测值和真实值之间的差异就越小,模型的预测精度就越高:

Table 6. Soil moisture prediction error table
表6. 土壤湿度预测误差表
从表6可以看出这四个放牧强度下的土壤湿度LSTM预测模型的误差值均很小,预测效果较佳。
4.4.4. 植被生物数量的模型
与土壤湿度相同,将选择后的植被生物数量影响因素数据带入上述步骤中去,可以得到不同放牧强度下植被生物数量的LSTM预测模型图6和预测误差值表7,从中可以看出植被生物数量LSTM时间预测模型的整体效果较佳,预测精度也较高。

Figure 6. Predicted values and actual values of the number of vegetation organisms (from left to right, top to bottom corresponding to the four grazing intensities of control, light grazing, moderate grazing and heavy grazing respectively)
图6. 植被生物数量的预测值与真实值(从左到右从上到下分别对应对照、轻度放牧、中度放牧和重度放牧这四种放牧强度)

Table 7. Prediction error table for the number of vegetation organisms
表7. 植被生物数量预测误差表
5. 问题二:模型的建立和求解
5.1. 问题二分析
问题二是问题一的延续,主要是对不同放牧强度下2022~2023年不同深度的土壤湿度进行预测。因此,针对问题二的预测,主要分为以下两步(图7):
(1) 首先根据往年数据对土壤湿度的三个影响因素(降水量、平均露点温度和平均最大持续风速)做ARIMA模型,预测得到2022~2023年这三个影响因素的值。(2) 第二步其实是问题一LSTM模型的延续,将第一步预测得到的值输入到10 cm土壤湿度的LSTM模型从而得到2022~2023年10 cm土壤湿度的预测值。对40 cm土壤湿度而言,不仅需要考虑降水量、平均露点温度和平均最大持续风速这三个影响因素,也要考虑10 cm土壤湿度对40 cm土壤湿度的影响,因此建立的是这四个因素对40 cm土壤湿度的LSTM模型从而预测得到结果。以此类推,最后预测得到2022~2023年不同深度土壤湿度值。
5.2. ARIMA模型
5.2.1. ARIMA模型原理
差分自回归滑动平均模型(简称ARIMA模型) [7] ,是将自回归AR模型、移动平均MA模型和差分法相结合得到的一种时间序列预测方法,适用于解决经济学领域中众多实际问题,比如说非平稳时间序列。其原理是将非平稳时间序列转化为平稳序列,再将因变量的滞后值和随机误差项的滞后值等做回归。ARIMA(p,d,q)模型的一般形式为:
其中
为时间序列,p为自回归阶数,q为移动平均阶数,
为自回归模型系数,
为移动平均模型系数,
为白噪声序列,d为差分阶数。
ARIMA的建模过程分为以下:(1) 对数据绘制时间序列图,观察是否为平稳时间序列,若为非平稳时间序列,则不断进行差分直到转化为平稳数据序列。(2) 定阶过程:利用AIC信息和BIC信息进行判断,确定好模型的参数
。(3) 用搭建好的模型去预测未来时间下的结果。
本文前后分别介绍了LSTM和ARIMA两个非常常见的时间序列预测模型 [8] ,并作为本次题目的关键模型,在不同情况下分别使用。其主要区别为:(1) 模型结构:ARIMA是一种经典的统计模型,基于时间序列的自相关和移动平均性质建立模型。而LSTM是一种深度学习模型,它是一种循环神经网络的变体,具有记忆单元和门控机制,能够捕捉长期依赖关系。(2) 预测能力;由于LSTM具有记忆单元和门控机制,能够捕捉长期依赖关系,因此在处理具有较长时间依赖的序列数据时通常具有更好的预测能力。而ARIMA则适用于较短期的预测任务。
5.2.2. ARIMA模型估计与建立
以平均最大持续风速为例,建立平均最大持续风速的ARIMA模型,剩下两个影响变量(降水量、平均露点温度)同理。

Figure 8. Time series graph of average maximum sustained wind speed
图8. 平均最大持续风速的时间序列图
观察图8可知由平均最大持续风速的往年数据非平稳时间序列,并且具有较强的季节性,因此需要每次间隔12个月做差分来消除季节性,同时还需要进行1阶差分,将数据转化成平稳时间序列,再根据自相关ACF函数图9和偏自相关函数PACF图10判断出我们需要做ARIMA模型。
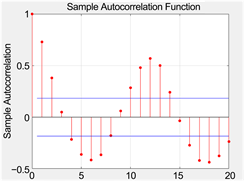
Figure 9. Autocorrelation ACF function graph
图9. 自相关ACF函数图
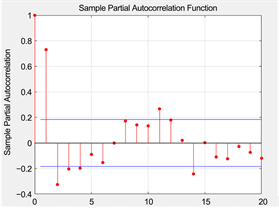
Figure 10. Partial autocorrelation PACF function graph
图10. 偏自相关PACF函数图
为防止模型出现过拟合现象,需要用信息准则判断模型参数,从而选择更简单的模型。通常选用AIC、BIC信息两个准则:① 赤池信息准则:
;② 贝叶斯信息准则:
,其中L为似然函数,
分别为参数和取样个数。
一般情况下信息越小,模型参数越好,因此根据信息准则表去选取AIC值和BIC值均最小的自回归阶数p和移动平均阶数q,最终选择的ARIMA模型为ARIMA(1,1,2) (如表8)。

Table 8. ARIMA information table
表8. ARIMA信息表
将平均最大持续风速的往年数据输入建立好的ARIMA(1,1,2)模型中,就可以得到2022~2023年平均最大持续风速的值:如表9(仅展示部分数据)。

Table 9. Average maximum sustained wind speed prediction values
表9. 平均最大持续风速预测值
5.3. 基于LSTM模型的预测
前面一步通过ARIMA模型求出平均最大持续风速、降水量等值。本文将平均最大持续风速、降水量和等往年数据作为训练集建立出10 cm土壤湿度的LSTM时间预测模型,再输入这三个因素2022~2023年的数据,最终预测得到2022~2023年10 cm土壤湿度的值。
由于40 cm土壤湿度不仅受到平均最大持续风速、降水量和平均露点温度的影响,也会受到10 cm土壤湿度的影响,因此需要建立平均最大持续风速、降水量、平均露点温度和10 cm土壤湿度这四个变量对40 cm土壤湿度的LSTM预测模型。同样100 cm土壤湿度也会受到40 cm土壤湿度的影响,以此类推,基于LSTM模型的预测,就可以得到2022~2023年不同深度下土壤湿度的预测值。
然而在模型训练过程中,本文发现,LSTM模型对土壤湿度预测效果始终不佳,在对模型进行多次调参后,得到最优的40 cm土壤湿度训练结果,拟合效果不佳,得到的精度较低,如图11所示。因此需要思考LSTM模型是否为本次问题的最佳模型。经过分析后发现,造成这一现象的主要原因是在预测过程中先对特征变量进行预测,再用预测后的变量值对土壤湿度值进行预测,用预测值去预测未知值会增加模型的误差,从而使得模型拟合效果不佳。并且此次任务为较短期的预测任务,并在后续的数据分析中发现土壤湿度的数据特征和平均最大持续风速几乎趋于一致,符合ARIMA模型,因此优先选择 ARIMA模型。
本文通过数据分析发现,土壤湿度的数据特征和平均最大持续风速几乎趋于一致,符合ARIMA模型,模型的建立与求解基本相同,因此本文将不在此赘述,通过建立不同土壤湿度的ARIMA模型预测得到2023年不同湿度下的土壤湿度值(表10) (仅展示部分数据):

Table 10. Predicted values of soil moisture at different moisture levels
表10. 不同湿度的土壤湿度预测值
6. 问题三:模型的建立和求解
6.1. 问题三分析
本题以放牧强度、小区为一个单位,需要分别建立年份与SOC土壤有机碳等5个土壤化学相关因子的多元线性回归预测模型,并预测不同单位下2022年的土壤相关化学因子的值。因此分为以下两步:(1)模型建立:一般情况下土壤性质变化受到时间的影响较大,且存在较强的线性关系,因此建立这5个土壤化学相关因子与年份之间的多元线性回归模型来进行求解。(2) 模型优化:对第一步建立好的模型进行评价时发现拟合效果并非最佳,因此考虑这5个土壤化学相关因子单独对年份做线性回归模型。
6.2. 多元线性回归模型
6.2.1. 多元线性回归模型原理
多元线性回归是多元统计分析里极其重要的分析方法之一,在实际中,一个元素的的变化常常受到多个变量因素的影响,为解释这一现象,通常采用多元线性回归模型,来描述一个因变量与其他多个自变量之间的相关关系。一般来说,多元线性回归模型的表达式为:
其中,
为因变量,有m个自变量
,
为回归系数,
为随机误差,
。写成矩阵形式:
。在服从正态分布的假设下,如果
满秩,那么回归系数
的最小二乘估计是:
。因此Y的估计值
,从而得到残差
,则随机误差方差
的最小二乘估计为:
在求解多元线性回归模型时,我们是根据残差平方和达到最小来找到最合适的回归参数
。
6.2.2. 数据处理
(1) 假设年份为因变量,5个土壤化学相关变量为自变量,符号如表11所示:

Table 11. Soil chemistry related symbols table
表11. 土壤化学相关符号表
(2) 由于试验设计采取随机区分组形式,实验者每年在每个放牧小区将每个放牧强度都设置了3个重复,因此对每个放牧小区和放牧强度下的5个土壤化学相关变量都取平均值来替代。下面举例G12、LGI的平均值取法(表12) (红色部分代表所求平均值):
6.2.3. 多元回归模型的求解
本题利用Matlab针对不同放牧强度及小区分别去求解年份与5个土壤化学相关变量的多元线性回归模型,由于有12种放牧小区,因此可以建立出12个多元线性回归模型。
基于模型计算得到多元线性回归方程为(以放牧小区G17、放牧强度NG为例):
同理可得不同放牧强度下12个放牧小区的多元线性回归模型。为验证模型的拟合效果,利用 值和置信区间去检验每个多元线性回归模型的回归系数,发现P值几乎都远远大于0.05,在统计意义上说明做的多元线性回归模型拟合效果并不好,为此下一步会对多元线性回归模型进行优化。表13为四种不同放牧强度下随机选取的一个放牧小区的多元线性回归系数的P值和置信区间表(仅展示对照组的数据):

Table 13. Confidence table for control group
表13. 对照组置信表
6.3. 多元线性回归模型的优化
我们观察每一个散点图可以发现在不同放牧强度和不同放牧小区的情况下,5个土壤化学相关变量分别对年份具有一定的线性关系,因此可以考虑针对这12个放牧小区,分别建立5个化学土壤相关变量对年份的线性回归方程。
在不同放牧强度和不同放牧小区的情况下,利用Matlab软件分别建立5个土壤化学相关变量对年份的线性回归方程:
(其中K为回归系数,b为常数项)。以单个放牧小区和放牧强度为一个放牧点,总共可以得到60个线性回归模型。
以放牧小区G12、放牧强度LGI为例,可以计算得到5个线性回归模型:
,
,
,
,
。
同理对剩余的放牧点做线性回归方程,得到不同放牧小区和不同放牧程度下5个土壤化学相关变量分别对年份的线性回归系数表14(仅展示部分数据):

Table 14. Regression coefficient table of soil chemistry related variables
表14. 土壤化学相关变量的回归系数表
建立好模型后预测得到12个放牧小区2022年在不同放牧强度下土壤化学相关变量的值,最终结果如表15所示(仅展示部分数据):

Table 15. Predicted values of soil chemistry related variables
表15. 土壤化学相关变量的预测值
7. 问题四:模型的建立和求解
7.1. 问题四分析
问题四是要求在给定的沙漠化程度指数值和土壤板结化定性模型下,求出这两者值最小的放牧策略,因此需要分别对沙漠化程度指数和土壤板结化定性指数进行分析 [6] [7] :
(1) 第一步主要是求出沙漠化程度指数预测模型表达式中的
值,表达式如下:
其中SM为沙漠化程度指数,
为调节系数,
为第i个指标因子的因子强度,
为第i个因子对沙漠化程度的贡献度,
为第i个因子权重系数。为计算出
的值,首先需要计算出每个指标因子的因子强度
和因子权重系数,从而求得每个指标对沙漠化程度的贡献值
。最后对沙漠化程度SM和贡献值
做线性拟合得到
的值。
(2) 第二步目的是求出不同放牧程度下土壤板结化程度值,为此需要先根据题目给出的定性数学模型
建立模型求解,以土壤蒸发量作为土壤板结化的表征,建立土壤湿度、容重和土壤有机物等四个变量对土壤板结化的线性回归模型,再将不同放牧强度下的数值输入模型中去,得到四种放牧强度下土壤板结化程度值,绘制线性图去判断出在轻度放牧强度下的土壤板结化最小。
7.2. 沙漠化程度指数
7.2.1. 因子强度
结合前人研究,现代的沙漠化过程主要受自然因素于人文因素的影响,其中自然因素又可以分为气象因素和地表因素两方面。本文首先选定气象因素中气温、风速、降水 [9] ;地表因素中的植被指数、地表水资源、地下水位,以及人文因素中的人口数量、牲畜数量 [10] 、社会经济水平共九个特征因子用以表征沙漠化程度。其中气象因素均以月平均数据表征,地表水资源和地下水位分别以地下10 cm、地下200 cm土壤湿度表征。人文特征分别以统计年鉴中牧区人口数量,牲畜数量以及牧区人均经营性收入数据表征 [11] 。
由于其中有4个指标因子的数据存在过多缺失值,直接删除。至此,基于统计年鉴表和附件数据得到5个沙漠化相关指标因子的值,如表16所示(仅展示部分数据):

Table 16. Desertification related indicator factor values
表16. 沙漠化相关指标因子值
为判断这9个因子的因子强度(
取值范围为
),主要分为以下两步:
① 单位标准化:使得这5个指标因子的统计年鉴数据单位与因子分级标准表中的单位相统一,比如统计年鉴表里的风速单位为knots,需要统一为m/s。② 因子强度分级:针对因子强度的分级界定,本文参考文献 [12] 量化特征因子的强度。具体量化公式如下:
其中c为特征因子的实测值,
分别为特征因子影响沙漠化的上下限取值。
本文参考联合国关于影响沙漠化特征因子的分级标准和相关文献,给出如表17:

Table 17. Factor upper and lower limit table
表17. 因子上下限表
经过数据处理后可以得到这5个指标因子的因子强度表如表18(仅展示部分数据):

Table 18. Factor intensity table of desertification related indicators
表18. 沙漠化相关指标的因子强度表
7.2.2. 因子权重系数和因子贡献值
得到沙漠化指标因子的因子强度后,需要对因子强度计算因子权重系数。常见的权重计算方法有因子分析、主成分分析和层次分析等,但因子分析主要利用信息浓缩原理,且其“旋转”功能使得因子具有更强的解释意义,因此在计算因子权重系数上选取因子分析法。因子分析法最早由英国数学家斯皮尔曼提出的一种基于降维思想的统计分析方法,它通过研究变量之间的相关系数矩阵,基于数据信息浓缩原理利用最大方差法对载荷因子进行旋转得到因子模型,计算因子得分从而得到权重系数,图12为因子分析模型:
因子分析的基本步骤主要分为以下4步:
(1) 首先将数据标准化处理,为消除数据间的量纲影响。(2) 使用方差最大化旋转对处理好的数据做因子分析。(3) 计算每个主因子得分和方差贡献率
,计算公式为:
,其中
为主成分,
为各个指标因子,
为各个指标因子在每个主成分里的系数得分。(4) 求出各个指标因子的权重,计算公式为:
。
将这5个指标因子(植被指数、平均气温和降水量等)的因子强度做因子分析,可以得到因子权重系数表19:

Table 19. Factor weight coefficient table of desertification related indicators
表19. 沙漠化相关指标的因子权重系数表
得到因子强度和因子权重系数后,根据表达式中的
,可以计算出因子对沙漠化程度的贡献值总和如表20(仅展示部分数据):

Table 20. Contribution value table of desertification related indicator factors
表20. 沙漠化相关指标因子的贡献值表
7.2.3. 沙漠化程度指数
由于缺少锡林郭勒盟沙漠化程度指数的数据,本文参考相关文献 [13] ,以绿植覆盖率表征沙漠化程度指数。

Table 21. Standard table for classifying desertification degree and desertification degree index
表21. 沙漠化程度及沙漠化程度指数划分标准表

Table 22. Table of criteria for classification of desertification types
表22. 沙漠化类型划分标准表
绿植覆盖率越高,沙漠化程度越小。对比表21和表22,本次问题将沙漠化程度指数选定为SM = 1− 绿植覆盖率,得到如表23(仅展示部分数据):

Table 23. Desertification related data table
表23. 沙漠化相关数据表
已知SM和
的值,结合公式
对调节系数
进行线性拟合得到
。对拟合结果进行验证,发现P值(P = 0.0049)远远小于0.05,具有较高的统计学意义。求出
的值后最终得到沙漠化程度指数预测模型表达式为:
7.3. 土壤板结化程度
已知土壤板结化程度与土壤湿度、容重等有关,土壤板结化程度的定性数学模型为
,其中W为土壤湿度,C为土壤容重,O为土壤有机物。土壤湿度越小,土壤容重越大,土壤有机物越少,则板结化程度越严重 [14] 。
7.3.1. 模型的建立
首先对数据进行处理(由于土壤容重为固定值1.39,因此数据部分将不对土壤容重进行处理):(1) 土壤板结化程度:由于土壤板板结化程度越严重会导致土壤蒸发量越低,因此在计算过程中本文均用土壤蒸发量代替土壤板结化程度。然后对土壤蒸发量进行[0,0.6]归一化处理,得到土壤蒸发量系数,则土壤板结化程度 = 1 − 土壤蒸发量系数。(2) 土壤有机物含量 = SOC土壤有机碳 + SIC土壤无机碳。
表24为土壤板结化程度的相关变量数值(仅展示部分数据):

Table 24. Numerical table of variables related to the degree of soil compaction
表24. 土壤板结化程度的相关变量数值表
(3) 皮尔逊相关系数分析:
为验证选出来的相关变量与土壤板结化程度的确有一定程度上的关系,因此得到皮尔逊相关系数表25:

Table 25. Pearson correlation coefficient table
表25. 皮尔逊相关系数表
然后利用Matlab软件建立得到土壤容重、全氮x1、10 cm土壤湿度x2、土壤有机物x3这4个变量对土壤板结化程度的多元线性回归模型:
。
得到多元线性回归模型后,再对模型的回归系数做验证,发现 值几乎都小于0.05,符合统计学意义上的相关性。同时得到模型的残差图13,发现拟合效果较佳,因此后续求解不同放牧强度下的土壤板结化程度都使用这个多元线性回归模型。
7.3.2. 模型的求解
由于题目要求在土壤板结化的基础上给出放牧策略,因此针对这一问题,需要分别将不同放牧强度下的土壤容重、全氮x1、10 cm土壤湿度x2、土壤有机物x3这4个变量的数据输入到土壤板结化程度的多元线性回归模型:
,得到四种放牧强度下的土壤板结化程度表(表26)和数据图(仅展示部分数据):
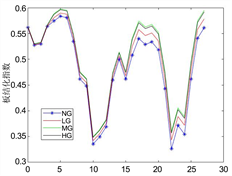
Figure 14. Map of soil compaction degree under different grazing intensities (NG is control, LG is light grazing, MG is moderate grazing, and HG is heavy grazing)
图14. 不同放牧强度下土壤板结化程度图(NG为对照,LG为轻度放牧,MG为中度放牧,HG为重度放牧)
观察图14可以知道在轻度放牧强度的情况下的土壤板结化程度最小(由于NG为对照组故不予计入在内),因此基于沙漠化程度指数值和土壤板结化定性模型就可以得出当放牧策略为轻度放牧时,沙漠化程度指数与板结化程度最小。
8. 模型评价
8.1. 模型优点
(1) 本文在解决每一问题时都对数据进行预处理,提高数据高效性;
(2) 参考联合国关于影响沙漠化特征因子额分级标准等文献,选取影响草原生态的关键特征,提高特征选择的有效性、降低实际挖掘所需有效影响因子的时间;
(3) 本文在分析解决问题时,充分考虑数据特点,并使用多个模型进行比较检验,选取最优解。
(4) 模型的计算成本低。
8.2. 模型缺点
(1) 由于时间紧张,在第二问中本文只依据LSTM模型对10 mm、40 mm处土壤湿度预测效果对其进行评价,具有一定片面性,同时未对其进行优化,后续可考虑组合模型对LSTM的初步预测结果中的残差进行训练拟合,从而提高模型的预测效果;
(2) ARIMA模型在预测数据时仅考虑时序关系,忽略了实际生活中其他因素如新冠疫情等突发情况对草原发展变化的影响。