1. 引言
现行各个版本的高中物理教材都编有机械波折射内容,并都仿照光的折射给出机械波折射的类似定义,即波由一种介质进入另一种介质时传播方向发生改变的现象称为波的折射。其中,有几种教材 [1] [2] [3] 还特别以水波为例,并认为水波在深水区跟浅水区的交界处发生折射的根本原因是深水区和浅水区是两种不同的介质。
各地一线教师在教授水波折射这一知识点的课堂教学以及一些网站或自媒体平台 [4] [5] [6] [7] 上传这一知识点的教学课件或教学视频,也都基本持这种观点。
事实上,水波是很复杂的一种机械波。为了厘清水波折射的根本原因,本文根据物理海洋工程学的相关知识体系对水波的传播特点进行一定研究,同时结合实验室方法给出水波折射的概念并予以解释。
2. 水波的深度认识
水波是依靠自身的表面张力、自身所受重力以及地转偏心力等共同作用传播的水面波,属于非弹性波。因此,水波跟其它机械波比如声波的传播特性不尽相同。同时,水波跟所有机械波一样,本质均不同于电磁波。根据水波波长跟水的深度的大小关系,通常将水波分为深水波、有限深水波和浅水波。如果水波的振幅小于水的深度,水波的传播不受水底部(海底、池塘底部等)影响,则称为深水波,否则称为
有限深水波或深水波。通常根据相对水深即水的深度h与水波波长
之比
来划分,一般地:当
时为深水波,也称为短波;当
时为浅水波,也称为长波;当
时为有限深水波。
为了使问题简化,以下的讨论将水波视为理想规则波动。因此认为:水为均质无可压缩(密度为常量)的无黏性的理想流体;水波引起的水运动是连续无旋的;自由水面压强均匀且为常量;作用在水上的质量仅受重力,表面张力和地转偏向力等均忽略不计。
2.1. 水波的频散关系和波速
根据线性波理论 [8] ,水波线性波动的势函数和波面方程可分别表示为
(1)
(2)
其中,
为圆频率,
称为波数,A为振幅,下同。在一定约束条件下,
、k、h之间满足
(3)
即是
(4)
这一表达式称为线性波动的频散方程,也称为线性波动的频散关系。将
和
代入(4)式,
可得线性波动的波长和波速分别为
(5)
(6)
由(5) (6)两式可以看出,当水深给定时,水波的周期越长,波长也就越长,波速(波形移动速度)也将越大。这样,不同波长的水波在传播过程中逐渐分离开,这种现象称为水波的频散现象。只有满足(4)的频散关系,水波才能稳定传播。
2.2. 深水波和浅水波的特殊性
1) 深水波
当水深h或波数k趋于无穷大即深水条件时,有
(7)
这时,(4) (5) (6)式可分别简化为
(8)
(9)
(10)
因此,在深水情况下,水波的波长和波速只与波动的周期有关,与水的深度无关,水底对深水波的传播不存在摩擦阻力的影响。
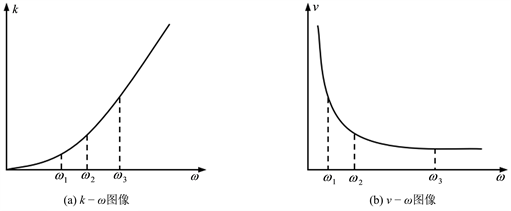
Figure 1. Parameter variation relationship of deep water waves
图1. 深水波的参数变化关系
事实上,当
或
时,(7)式已经足够精确。所以,通常当水深大于或等于波长一半即
的波均可视为深水波,其参数变化关系可用如图1所示的
图像
图像表示。
2) 浅水波
当水深h或波数k趋于0即浅水条件时,有
(11)
这时,(1) (4) (5) (6)四式可分别简化为
(12)
(13)
(14)
(15)
因此,在浅水情况下,水波的传播速度只与水的深度有关,与水波的性质(周期或波长)无关。也就是
说,任何水波传到浅水区后,其传播速度只受水深控制,波动不再具有弥散性质。通常情况下,水深
或
时的水波就可视为浅水波,其参数变化关系可用如图2所示的
图像
图像表示。
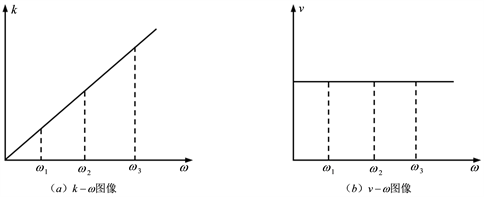
Figure 2. Parameter variation relationship of shallow water waves
图2. 浅水波的参数变化关系
2.3. 水质点运动的轨迹
研究表明,任意水质点
相对于其平衡位置
运动的轨迹方程可表示为
(16)
不难看出,这是一个椭圆的标准方程。因此,(16)式表明水质点运动的轨迹是一个椭圆。该椭圆的半长轴为水平方向,半短轴为铅垂方向,半长轴和半短轴的大小都随水的深度(−z)的增加而减小,半长轴变化较慢,半短轴变化较快。在水底处,半短轴为0,水质点只做水平运动。
因此,水波波动过程中,不仅只是水面的水质点参与运动,而是波动区域内的几乎所有水质点都参与运动,不同深度处的水质点运动的速度(非波形移动速度即波速)随着水的深度(−z)增加而以指数函数规律迅速减小。每个水质点均同时具有水平向速度和铅直向速度,但铅直向速度远小于水平向速度。
对于深水波,(16)式可以简化为
(17)
这一式子表明,深水波中水质点的运动轨迹是一个圆,其半径随水的深度(−z)的增加而减小,当达到一定深度时,当达到一定深度时运动消失,如图3(a)所示。
对于浅水波,(16)式可简化为
(18)
这一式子表明,浅水波中水质点的运动轨迹仍是一个椭圆,但半长轴不随水的深度(−z)变化,而半短轴相对于半长轴很短并随水的深度增加而减小,如图3(c)所示。同时不难理解,水质点的铅直向速度随着水的深度(−z)的增加而减小,而水平向速度的大小与水的深度无关,同一铅垂线上的各点从水面到水底,水平向速度均相等。
对于有限水深水波,水质点的运动轨迹也是椭圆,但其半长轴和半短轴都随着水的深度(−z)的增加而减小,但介于深水波和浅水波之间,如图3(b)所示。
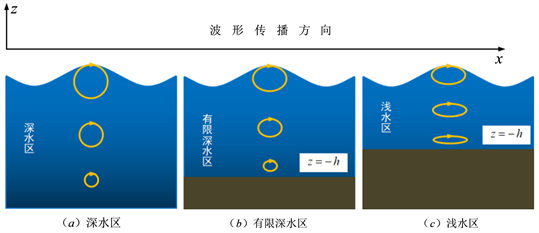
Figure 3. Movement trajectories of water quality points in different water area
图3. 不同水区水质点的运动轨迹
2.4. 水质点运动与波速的关系
波速公式(6)式表示的波速是指整个波形向前移动的速度,并非水质点移动速度。也就是说,波形以一定的速度向前传播(称前进波,区别于驻波),而不是水质点的传播,各水质点只围绕各自的静平衡位置作椭圆周运动或圆周运动。波形向前传播完全是由水质点运动而产生的,但是二者并非同一概念。就像麦田中麦浪滚滚向前,而麦株并不跟着向前运动。
现以深水波为例,用沿波面水质点的速度分布,说明水质点运动与波速之间的关系。根据深水波水质点运动的轨迹方程即(17)可得到深水波水质点的水平向速度和铅垂向速度方程分别为
(19)
(20)
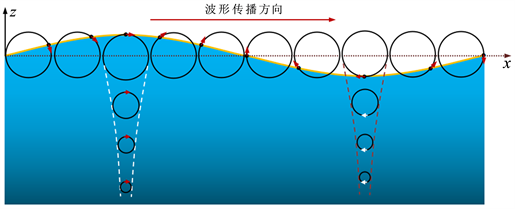
Figure 4. Relationship between water quality point movement and wave velocity
图4. 水质点运动与波速之间的关系
现以深水波为例,用沿波面水质点的速度分布,说明水质点运动与波速之间的关系。如图4所示,
由波面方程(2)式和水质点的运动速度方程(19)式可知,位于波峰以及波峰(
)以下的水质点,具有正向水平最大水平向速度,铅垂向速度为0;位于波谷(
)以及波谷以下的水质点,具有
负向水平最大水平向速度,铅垂向速度也为0;位于波面与静止水面交点以及该点以下的水质点,水平向速度为0,铅垂向速度最大。同时还可看出,位于波峰前部的水质
点,速度均向上;而位于波峰后部的水质点,速度均向下。因此无论何时,波峰前部都是水质点的的辐聚区,波面将向上,波峰也将随之向前移动;波谷前部(波峰后部)都是水质点的辐散区,波面将向下,波谷也将随之向前移动。这样,从而使波形不断向前传播,而各水质点只围绕自身的平衡位置作圆周运动。
2.5. 水波的本质
根据水波波面质点的运动的椭圆形轨迹或圆形轨迹可知,水波传播过程中,其波面质点同时参与跟传播方向垂直的振动和跟传播方向平行的振动。因此,水波既不是横波,也不是纵波,而是一种兼有横波和纵波某些特点的复合波,水波的波面以及波面以下均是由无数的微小涡流组成的动态结构。
3. 水波折射的本质原因
水波的传播实际上是很复杂的,与水的深度等诸多因素有关系。同一列水波在深度不同的水域传播时,其波高(波峰到波谷的垂直距离即相当于两倍振幅)、波长、周期和波速等都不尽相同。
3.1. 波高、波长与波速的变化
如图5所示是一列水波由深水区进入浅水区(波向线垂直于等深线)的剖面情景,从图中可以看出,水波由深水区进入浅水区,其波高增大而波长减小。这是因为水波由深水区进入浅水区后,由于受到分界台阶及浅水底摩擦等因素的阻碍,使得水波的水势升高即势能增大,因而波高增大。根据能量守恒原理(实际能量有所损失但不影响对问题的分析),水波由深水区进入浅水区后,动能必然减小,波速变小,因此波长减小。
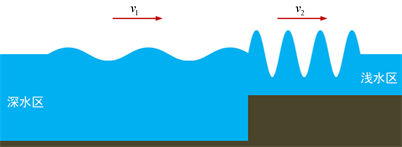
Figure 5. Water waves entering shallow water from deep water
图5. 水波由深水区进入浅水区
3.2. 水波的折射
在水波由深水区进入浅水区时,如果波向线(传播方向)跟分界线或等深线(水深度相等的点构成的线)不垂直,由于分界台阶及浅水底摩擦等因素的阻碍引起水波传播波速发生了变化,导致水波的传播方向也会发生改变,这种现象称为水波的折射。如图6所示是用某型号的方形水波槽进行水波折射实验得到的水波折射照片。假设水波在深水区和浅水区的速度分别为
和
,入射角和折射角分别为
和
。可以证明水波的折射跟光的折射遵循相类似的斯涅尔公式(折射定律),即
(21)
其中,这里的折射率n跟水的深度有关,还跟水波槽的形状大小有一定关系。
实践表明,水波由浅水区进入深水区时,由于深水区水底的摩擦等因素的阻碍作用减弱或消逝,水波的水势将降低势能减小,从而水波的波高减小波长增大动能增大波速变大。因此,水波由浅水区进入深水区同样会发生折射,但这种情况在实验室中观察的难度要大一些。
3.3. 水波折射的解释
如图7所示是一列平面水波的两条平行波线由深水区进入浅水区发生折射的波路,其中EF是分界线,同时也是一条等深线。深水区中波速为
、两波线之间的距离为
,浅水区中波速为
、两波线之间的距离为
,A和B、
和
、
和
、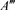 和
分别处在同一波阵面上。根据惠斯通原理,一波线上的波元质点的振动模式由A点依次传播到
、
及
点的过程中,另一波线上的波元质点的振动模式相应由B点依次传播到
、
和
点。显然,若令一波元质点的振动模式由
传播到
的时间为dt,那么另一波元质点的振动模式由
传播到
的时间也为dt。设
和
跟分界线之间的夹角(容易证明等于入射角)分别为
和
,那么有
和
分别处在同一波阵面上。根据惠斯通原理,一波线上的波元质点的振动模式由A点依次传播到
、
及
点的过程中,另一波线上的波元质点的振动模式相应由B点依次传播到
、
和
点。显然,若令一波元质点的振动模式由
传播到
的时间为dt,那么另一波元质点的振动模式由
传播到
的时间也为dt。设
和
跟分界线之间的夹角(容易证明等于入射角)分别为
和
,那么有
(22)
及
(23)
若令折射率为n,则由(22) (23)两式,容易得到
(24)
这就证明了水波折射遵循的斯涅尔公式(折射定律)。
4. 结论
1) 水波折射过程中,深水区和浅水区的水结构以及杂质成分等没有任何变化。因此,将深水区和浅水区视为两种不同的介质的这种观点是完全错误的。
根据(24)式,由于
,所以
,即
。说明波阵线由深水区跨过分界线(等深线)进入浅水区的过程中,有逐渐与分界线(等深线)平行的趋势,也就是波线有逐渐与分界线(等深线)垂直的趋势。这正是在海岸上观察从深海传过来的海浪,到达近岸时波阵线总是大致与海岸平行,海浪总是扑面而来的原因。
2) 只考虑水质点的自身重力作用而没有考虑水的表面张力等因素影响的水波常称为重力波。如果考虑水的表面张力影响,那么深水中的水波速度即(10)式可改写为
(25)
其中,
为水的表面张力系数,
为水的密度。
3) 在深海中,若由于风力等作用先后产生波长不同的几列水波,且后波的波长大于前波的波长,如图8所示。根据(10)式,由于后波速度大于前波速度,即图中
,因此几列波将可能会同时到达同一位置,因而叠加形成大浪或巨浪。
Figure 8. Several columns of water waves with different wavelengths in the deep sea
图8. 深海中几列波长不同的水波
基金项目
2022年教育部高等学校大学物理课程教学指导委员会大中物理教育衔接工作委员会教学研究课题“三新背景下县域普通高中物理实验教学策略研究”(立项编号:WX202242)部分研究成果。