1. 引言
传递损失(TL)是反映消声器实际降噪量的重要指标,由于实际测量较为复杂,因此对传递损失的研究基本以理论分析和有限元分析为主。国内外对消声器传递损失的计算方法已有较多研究,早期应用最广泛的是一维传递矩阵法,该方法只适用于低频简单平面波的传递损失预测。1974年Young和Crocker [1] 利用拉格朗日函数法和矩阵单元对简单膨胀腔进行分析,首次提出了预测消声器传递损失的有限元方法。1981年Ross [2] [3] 通过引入子结构分析方法,将两个扩张腔并联的消声器分为两个子系统进行处理,节省了计算时间。2005年Omid Z和Marius [4] 用三维有限元方法建立了预测消声器传递损失的模型,并提出了穿孔板和多孔材料在有限元中的等效方法。近年来已有利用商业有限元软件对消声器传递损失进行的研究,Fu [5] [6] 利用有限元法对消声器的参数、结构进行改进。温华兵等 [7] [8] 利用有限元软件对消声器传递损失预测并验证的同时还对消声器结构进行了改进设计。陈志响 [9] 和唐焱 [10] 对消声器内部流场进行了仿真。Zhang等 [11] 对侧向开口的消声器传递损失预测进行了理论分析和实验验证。
现有的研究对象大多是体积较小的抗性消声器 [12] [13] 和结构简单的阻性消声器 [14] [15] ,为了获得消声器的传递损失,可以利用商业有限元软件直接计算其空气通道的传递损失。大型工业消声器侧壁处的二次辐射噪声不可忽略,计算传递损失时必须考虑侧壁传声的影响。而目前的商业有限元软件中没有公式可以直接计算侧向透过管壁的声能量,因此对结构复杂的大型工业消声器,有限元的传递损失计算结果会远大于实测插入损失。
为了解决大型消声器侧壁传声难以估计的问题,本文给出了一种侧壁传声的预测方法。利用模态分解法 [16] [17] 计算管壁透射声功率,并探究侧壁传声的影响因素,拟合出能够快速估计消声器侧壁传声的公式。最后探究侧壁传声对消声器插入损失的影响,结合COMSOL软件得到考虑侧壁传声的插入损失,并通过实验进行验证。
2. 侧壁传递损失的计算方法
2.1. 侧壁透射声功率的推导
如图1所示,首先考虑一半无限长的薄壁圆柱壳,半径为α,径向坐标为r,极角为θ,轴向坐标为z。
分别对应管壁的轴向、周向和径向位移。根据Donnell-Mushtari壳理论 [18] ,圆柱壳径向位移响应为

Figure 1. Schematic diagram of cylindrical pipes and coordinates
图1. 圆柱形管道及坐标示意图
(1)
(2)
(3)
其中Wnm为径向振动位移的模态幅值,
和
分别为径向波数和轴向波数,二者满足
。n代表周向模态数,对于每一阶周向模态,都对应了m阶径向模态。无量纲频率
,截面回转半径
,无量纲轴向波数
。
在
处,管内径向声压和向外透射的声压为 [19]
(4)
(5)
式中Jn表示宗量为
的n阶贝塞尔函数,
表示宗量为
的n阶第二类汉克尔函数。
和
分别是管内、管外声压的模态幅值。
假设声源位于管口(z = 0)处,其表面的振动速度可以在柱坐标系下模态展开为 [20] [21]
(6)
方程两边同乘
并积分,可以定得系数为
(7)
(8)
由轴向速度连续可以推出管外壁透射声压的模态幅值:
(9)
(10)
(11)
其中,ρ0为空气密度,
表示
对
求导
因此管壁外侧径向质点速度为
(12)
考虑侧壁面积为S的有限长管道,透射声功率为
(13)
为了方便工业上对消声器侧壁传声影响的评估,将管道侧壁的传递损失定义为通过侧壁前后的声功率损失,即:
(14)
其中,
表示管道入口处声功率,
表示管壁透射声功率。
2.2. 侧壁传递损失及工程估算公式
接下来探究管道半径大小以及声源位置、点声源数量对侧向传递损失的影响。在此基础上,通过拟合给出消声器侧向传递损失的工程预测公式。
2.2.1. 参数影响
管道半径r范围0.3~1 m,频率f范围500~4000 Hz,利用公式(1)~(13)计算各频率下不同半径的消声器侧向传递损失R,探究r对R的影响规律。结果如图2,管道尺寸对侧向传声的影响较大,侧向传递损失的最小值出现在管道环频附近。

Figure 2. Effect of pipe radius on lateral transfer losses
图2. 管道半径对侧向传递损失的影响
在z = 0的平面上,将点声源分别摆放在圆心与管壁之间的不同位置,声源表面振速幅值不变,探究声源在管中位置的影响。其次在管口布置不同数量的点声源,假设它们的幅值与相位均相同,探究点声源数量的影响。结果如图3所示,点声源的位置和数量对侧向传递损失的影响较小,不考虑为影响因素。
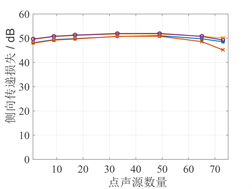
 (a) 声源位置的影响 (b) 点声源数量的影响
(a) 声源位置的影响 (b) 点声源数量的影响
Figure 3. Effect of sound source parameters on lateral transmission loss
图3. 声源参数对侧向传递损失的影响
2.2.2. 拟合公式
公式(1)~(13)的方法计算侧向透声的过程较为复杂,工程应用中希望有一个简单的计算公式。圆柱壳的隔声量主要与质量、环频、吻合频率和声波的入射方向相关,参见文献 [22] 。给定圆柱壳的结构材料和尺寸,质量、环频、吻合频率容易计算得到,但声波入射方向的影响难以精确计算。可以通过解析数据拟合的方式予以估计,假定管壁侧向传递损失具有如下形式:
(15)
式中
为环频,单位Hz;
为吻合环频,单位Hz;f目标频率,单位Hz;r消声器半径,L消声器长度,单位m。r/2L为管口横截面积与侧壁表面积之比。mshω代表质量的影响。h管壁厚度,单位mm。ρ材料密度,E杨氏模量,D弯曲刚度。
利用MATLAB中的ploy fit函数通过“最小化误差的平方和”寻找与计算结果匹配的最佳函数,使得求得的表达式与计算数据之间误差的平方和为最小。求出式(15)中α1= 1.02,α2= 0.021,α3= 0.011,α4= 3。该公式的适用范围
,
,
,
。
为了验证拟合公式的准确性,将计算结果和拟合结果对比。结果如图4,计算所有点的误差后取平均值,平均误差约为2 dB。

 (a) 频率500 Hz,板厚1 mm,长5 m (b) 频率1000 Hz,板厚1 mm,长5 m
(a) 频率500 Hz,板厚1 mm,长5 m (b) 频率1000 Hz,板厚1 mm,长5 m
 (c) 频率2000 Hz,板厚1.5 mm,长8 m(d) 频率4000 Hz,板厚1.5 mm,长8 m
(c) 频率2000 Hz,板厚1.5 mm,长8 m(d) 频率4000 Hz,板厚1.5 mm,长8 m
Figure 4. Comparison of calculated and fitted results (1/3-octave-band center frequency)
图4. 计算结果与拟合结果对比(1/3倍频程中心频率)
工程上,当公式(15)得到的侧壁传递损失与COMSOL得到的空气通道传递损失相比不小于2 dB时,建议考虑侧向传声的影响。
2.3. 考虑侧壁传声时插入损失的估计
消声器的传递损失(TL)反映噪声通过消声器后的声能损失。不考虑消声器的侧壁声能泄漏时,可以定义传递损失为消声器入口处的入射声功率级与出口处的透射声功率级之差,即
(16)
其中,
表示消声器入口处的声功率,
表示消声器出口处的声功率。
工程上,上述定义式虽然可以通过COMSOL等有限元仿真软件进行计算,但难以直接测量,常通过测量插入损失来代替。根据GB/T 4760-1995《声学–消声器测量方法》 [23] ,消声器插入损失的实验室测量方法是:在相同入射功率条件下,替换管出口的测量声功率级减去消声器出口的测量声功率级。即
(17)
其中,IL表示消声器的插入损失,单位dB。
,
分别为替换管和消声器出口端的声功率级,单位dB。替换管是指与待测消声器具有相同长度、相同通道截面和相同外壁材质厚度的空管道。由于替换管是空管,入口输入的声功率
等于出口输出的声功率
。因此在不考虑侧壁漏声时,公式(16)定义的传递损失在数值上等于公式(17)定义的插入损失。
但实际测量中,当侧壁振动引起的二次噪声不能忽略时,公式(17)中测得的
应该包含空气传声和结构传声的共同影响,即
(1)
其中
为入射噪声沿消声器空气通道传播至出口的声功率,该部分可以通过COMSOL等常用的商业有限元软件计算。
为结构振动二次噪声辐射引起的声功率,包括消声器侧壁向管内辐射的声功率和消声器下游连接管道向管内辐射的声功率。
由于消声器测试装置下游管道复杂,没有固定的标准,管壁振动引起的二次声辐射功率难以直接评估,如果可以假设结构振动在出口处引起的辐射噪声与消声器侧壁透射的噪声相当,则问题变得相对简单。由于结构辐射的声功率与结构均方振速成正比,即
(19)
其中,ρ0、c0分别为空气的密度和声速,σ为结构声辐射系数,
为均方振速,S为面积。假设替换管和下游连接管道的结构声辐射系数相等,则可以用公式(20)定义的均方振速级表示二者辐射噪声的差距。
(20)
其中,下标L表示下游连接管道,下标T表示替换管。
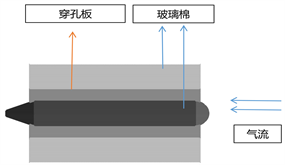
利用COMSOL软件计算替换管以及下游连接管道侧壁处的振动速度。替换管的直径1.6 m,长度为3 m,壁厚1.5 mm,连接管道的直径1.6 m,长度依次取3 m、5 m、7 m,管壁厚度依次取1.5 mm、3 mm、4.5 mm,对比相同尺寸的替换管和连接管道侧壁的振动响应,同时探究连接管道尺寸对其侧壁振速的影响。两个管道通过法兰连接,管道两端简支约束,材料杨氏模量E取2e11 × (1 + 0.01j) Pa。在COMSOL软件中对管壁沿周向施加分布线力载荷模拟管口声源对管壁的作用力,假设声源的声辐射在3 m长替换管两端的衰减达到40 dB,则在衰减为20 dB的位置前施加1 Pa~0.1 Pa递减的分布力,如图5所示。计算得到的100~8000 Hz倍频程下替换管和连接管道侧壁的均方振速级如图6所示。

Figure 5. Schematic diagram of replacement pipe and connecting pipe structure
图5. 替换管与连接管道结构示意图
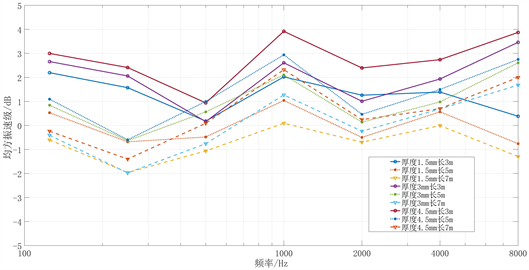
Figure 6. Comparison of mean square vibration velocity level at the sidewalls of replacement and connecting pipes. (octaveband frequency)
图6. 替换管和连接管道侧壁均方振速级对比(倍频程中心频率)
结果表明在替换管尺寸不变的情况下,公式(20)定义的均方振速级随着下游连接管道厚度的增大而增大,随管道长度增大而减小,并且差值小于2 dB。在环频1000 Hz附近,替换管和连接管道的振速差距略大,均方振速级最大约4 dB。上述计算表明,消声器侧壁辐射的倍频带声功率和下游连接管道侧壁向管内辐射的倍频带声功率差值在5 dB以内。由于空气通道插入损失的计算值和消声器插入损失的实测值的差值可在40 dB以上(参见图11),说明消声器出口声功率远远小于结构传声的声功率。在这种情况下,以消声器侧壁辐射的声功率代替下游连接管道侧壁向管内辐射的声功率作为修正是合理的。即可以假设:
(21)
因此插入损失的公式可以近似等效为:
(22)
上式中侧壁透射的声功率
可以通过公式(1)~公式(13)的方法计算,也可以结合公式(14)和简化的拟合公式(15)来计算。而空气通道出口处的声功率
可以通过COMSOL等商业软件计算得到。
3. 应用COMSOL计算空气通道的出口声功率和插入损失
3.1. 消声器模型建立
通过多物理场仿真软件COMSOL Multiphysics对消声器进行三维仿真,对于对称结构,可进行对称边界条件设置,即仅对一半的结构进行仿真计算,在不影响精度的前提下,极大提高计算效率。如图7(a)所示为采用二维轴对称模型建立的流体域。
3.2. 前处理设置
3.2.1. 定义流体属性
消声器的流体域应设置两种流体属性,一种为空气,另一种为玻璃棉。在声学计算中,玻璃棉作为多孔介质用Delany-Bazley-Miki模型进行表征,定义其比流体阻力率。
3.2.2. 定义出入口边界条件
使用端口边界条件来模拟消声器的入口和出口,在波导中,端口条件优于辐射条件,因为端口条件可以捕捉到涉及多种传播模式的复杂波场。设置入口处垂直入射波幅值为1 Pa。由于该消声器的求解频率高于管道内低阶模态波的截止频率,因此除了(0,0)阶平面波还需要考虑(0,1)、(0,2)、(1,0)、(2,0)、(1,1)、(1,2)等高次波 [24] 。出口设置为无反射边界。
3.2.3. 定义穿孔板
在COMSOL声学模块中,穿孔板可进行等效处理,根据穿孔板两侧的阻抗差对穿孔板的透声量进行模拟,这样在软件中通过设置边界条件即可实现对穿孔板的模拟。在压力声学接口中,赋予结构穿孔板边界为内部阻抗边界。
3.2.4. 网格划分
采用自由四面体单元对流体域进行网格划分,为保证计算精度,最大网格单元的尺寸应为最小波长的1/6。如图7(b)所示,本研究中计算的频率范围为100~10,000 Hz,因此最大网格单元大小为5.6 mm,单元数量为296,907。

 (a) 二维轴对称模型 (b) 声学网格
(a) 二维轴对称模型 (b) 声学网格
Figure 7. 2D axisymmetric model and acoustical mesh
图7. 二维轴对称模型和声学网格
3.3. 仿真结果和数据处理
对模型进行频域研究得到消声器入口和出口处的声压,如图8(a),进而计算出入口和空气通道出口处的声功率
、
,以及消声器空气通道的传递损失,如图8(b)所示,并通过公式(16)和(22)以及前面计算的
得到考虑侧壁传声后的插入损失。
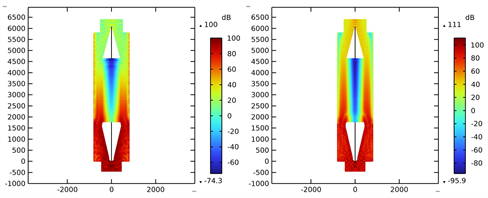 (a) 消声器声压级云图2000 Hz (左) 4000 Hz (右)
(a) 消声器声压级云图2000 Hz (左) 4000 Hz (右) (b) 消声器空气通道插入损失
(b) 消声器空气通道插入损失
Figure 8. Simulation results and data processing
图8. 仿真结果和数据处理
4. 实验过程
4.1. 实验系统组成
实验依据GB/T 25516-2010《声学–管道消声器和风道末端单元的实验室测试方法》 [25] 标准进行。测试系统由扬声器单元、测试直管管道、变径管、替换管、消声器、传声器和混响室组成,如图9所示。测试管道长度11,000 mm,试件前方和后方的管道由复合钢板制成。混响室容积241 m3,表面积234 m2,温度17℃,气压101,300 Pa。
 注:1-声源箱中的扬声器单元;2-试件前方的测试管道;3-变径管;4-替换管;5-消声器;6-试件后方的测试管道;7-混响室;8-传声器。
注:1-声源箱中的扬声器单元;2-试件前方的测试管道;3-变径管;4-替换管;5-消声器;6-试件后方的测试管道;7-混响室;8-传声器。
Figure 9. Schematic diagram of the experimental system
图9. 实验系统示意图
4.2. 实验方法
本测试系统以混响室作为声源的接收端,可以在无气流条件下对安装在测试管道中的消声器及替换管进行1/3倍频程声功率级的测量。扬声器单元发出的声源辐射经过消声器后进入混响室,混响室中的传感器测定相应的1/3倍频程声功率级数据,最后声源辐射通过混响室一端的管道排出。得到两种试件测得的1/3倍频程声功率级数据,两者的差值即为消声器的测量插入损失。
4.3. 消声器型号及参数
分别对四个结构和内部穿孔参数不相同的消声器进行了实验测试,其结构示意图见图10,详细参数见表1。

 (a) Ⅰ消声器 (b) Ⅱ消声器
(a) Ⅰ消声器 (b) Ⅱ消声器
 (c) Ⅲ消声器 (d) Ⅳ消声器
(c) Ⅲ消声器 (d) Ⅳ消声器
Figure 10. Schematic construction of four different mufflers
图10. 四种不同消声器结构示意图
5. 测量与计算结果对比分析

 (a) Ⅰ消声器 (b) Ⅱ消声器
(a) Ⅰ消声器 (b) Ⅱ消声器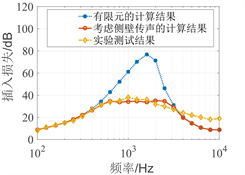
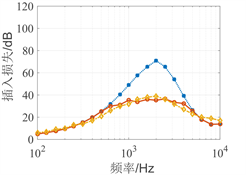 (c) Ⅲ消声器 (d) Ⅳ消声器
(c) Ⅲ消声器 (d) Ⅳ消声器
Figure 11. Comparison of insertion loss results (1/3-octave-band center frequency)
图11. 插入损失结果对比(1/3倍频程中心频率)
将考虑侧壁传声后的插入损失计算结果与COMSOL计算得到的消声器空气通道传递损失和实验结果进行对比,如图11所示。考虑侧壁传声的计算结果比COMSOL计算得传递损失大幅降低,说明大型工业消声器侧壁传声对插入损失的影响重大。考虑侧壁传声的计算结果与实验结果更为接近,验证了本文计算方法的可行性。
6. 总结
本文基于圆形声波导理论和模态展开法给出了一种消声器侧壁传声的预测方法,并结合质量、结构环频以及吻合频率给出了一个拟合公式,可在工程实践中对大型工业消声器的侧壁传声损失进行快速估计。研究发现当商业有限元软件计算的空气通道传递损失小于本文计算的侧壁传递损失时,需要计及侧壁振动二次声辐射引起的声能泄露影响。通过比较消声器和下游管道的侧壁均方振速,并依据空管计算的侧壁透射声功率对COMOSL计算的消声器插入损失进行了修正,修正后的传递损失比不考虑侧向传声时降低近40 dB,与实验测量结果相比,4000 Hz以下的平均误差小于3 dB。因此该方法可以正确预测消声器的侧壁传声,并显著提升了对插入损失预测的准确性。
基金项目
国家自然科学基金(12374447)。