1. 引言
1.1. 研究背景
股票市场是一个信息错综复杂,状态瞬息万变的市场。政治、经济、市场环境、政策环境、社会行为等都会影响股票价格的变动。因此,如何把握股票市场行情信息和资产价格走势,是股票投资者深入研究的课题。此外,如何通过交易策略获得投资收益也是当下长期热门的研究 [1] 。
尽管有效市场假说认为股票市场是不可预测的,但它仍然受到多种因素的影响,例如经济政策、行业趋势、公司管理等,这些因素都会影响股票价格。随着大数据时代的发展,研究人员开始将人工智能应用于这一领域,其中包括机器学习和深度学习技术 [2] 。然而机器学习预测方法存在一些局限性。相比之下,深度学习网络具有强大的特征学习能力,其网络层数更多,结构更复杂,能将数据中的浅层信息转化为更抽象的高特征信息,因此,深度学习对比机器学习,有更好的预测效果并且已经在许多领域得到应用 [3] [4] 。
深度学习目前广泛应用于股票价格预测领域,并产生了良好的结果。尽管使用这些方法在数据分析表现优异,但时间序列存在不稳定和随机性,以至于分析和预测时间序列依然具有挑战性。为了解决时间序列的存在的问题,研究者们提出了时序分解方法,以便于将时间序列分解成稳定且有序的子序列进行数据分析。经验模态分解(EMD)和CEEMDAN等时序分解方法可以作为降低时间序列复杂性的有用工具。这些方法可以很容易地将高波动数据分解为相应的较小信号分量。
1.2. 国内外研究现状
由于投资者关注股票价格未来趋势,准确预测股票价格一直是金融领域备受关注的话题。然而,这仍然是一个难以解决的问题,许多研究者投身其中,并已取得不错的成果。传统的股市预测方法主要集中于时间序列分析。De Gooijer等人 [5] 回顾了国际预报员协会和国际预报杂志期刊上发表的论文,发现其中超过30%的论文侧重于时间序列分析。这些方法包括自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)。然而,这些方法都重点关注时间序列本身,而忽略了历史数据对序列的影响。因此,研究者探索了新的方向,将机器学习和深度学习应用于该领域。
Hall等人 [6] 分析了人工神经网络(ANN)在约旦证券市场股票价格预测方面的可行性。Murat等人 [7] 利用MLP模型对道琼斯指数的大盘数据进行预测。陈佳 [8] 则利用循环神经网络模型(RNN)研究中国股票市场。Wang等人 [9] 使用LSTM神经网络并根据历史价格对股票价格进行预测,发现与其他人工智能算法相比,LSTM的预测能力更好。宋刚等人 [10] 将PSO与LSTM相结合,提出一种PSO-LSTM模型来预测股票价格,PSO算法对于神经网络有很好的优化效果 [11] 。
虽然上述方法在金融领域表现不错,但对于更为复杂的金融时间序列,普通的深度网络模型表现就不够出色。研究者发现时序分解方法与深度学习模型相结合,有很好的预测效果。Wang等人 [12] 将时序分解方法与PSO-LSTM模型相结合,发现时序分解方法能有效提高股票预测的精度。颜轲越等人 [13] 则用了不同的信号分解方法用于股票价格预测,发现CEEMDAN有很好的提升效果。
1.3. 研究方法
本研究将时间序列分析与深度学习模型相结合,提出了一种名为CEEMDAN-PSO-LSTM的模型,用于预测不同国家股票指数的收盘价格。首先利用CEEMDAN算法对原始股票价格时间序列进行时序分解,得到IMF。在LSTM模型的基础上,通过PSO,对LSTM网络的超参数进行寻优。然后各个IMF分别利用优化后的模型进行预测,最终将得到的各个预测值通过加和处理得到最终的预测值,该预测值就是模型对原始股票价格时间序列的预测结果。本文选取五个国家的其中一支代表性的股票指数作为测试数据集,对本文提出的预测方法和LSTM、PSO-LSTM、EMD-LSTM、CEEMDAN-LSTM这四个方法的预测结果进行对比实验,以此验证本文所提出方法的有效性和实用性。
2. 模型介绍
在本节,我们会详细介绍本文所提出的方法。我们将CEEMDAN,PSO,LSTM神经网络应用在股票预测领域,构建了一个名为CEEMDAN-PSO-LSTM的模型来预测股票价格指数。CEEMDAN-PSO-LSTM组合模型的股价预测流程图见图1。该混合模型主要分为PSO算法部分、CEEMDAN分解部分、LSTM神经网络部分以及模型评估部分。该模型的各部分描述如下:
1) 输入为原始股票指数的收盘价记作
,首先将其数据预处理后作为PSO算法的输入。本论文的数据预处理分为两步,其一是数据归一化,具体方法为MinMax归一化,其公式如下:
(1)
此时,式中的
为
,计算得到的
记作
。其二是划分数据集,将归一化后的数据集分割为训练集和测试集以及验证集,本实验训练集和测试集的选取规则为数据集的70%为训练集,30%为测试集,随机10%的数据集作为验证集。
2) 利用PSO算法优化LSTM神经网络超参数,具体步骤如下:1) 初始化粒子群参数。2) 初始化粒子的速度和位置。随机生成一个粒子,该粒子的位置为
,其中h为隐含层神经元个数,b为batch_size大小,l为学习率大小。该粒子的速度为
。3) 确定PSO算法的适应度函数。适应度函数值公式如下:
(2)
其中N为测试集的长度,
为输入数据。4) 比较适应度函数值并更新个体最优值和群体最优值。通过与初始位置的适应度值比较更新个体最优值
和群体最优值
,根据公式(3)和(4)不断更新粒子的速度和位置,直到达到最大迭代次数,确定最优位置,其参数h,b,l即需要优化的LSTM神经网络的超参数。获取最优参数。公式(3)和(4)如下:
(3)
(4)
其中,
为惯性权重;
,
为学习因子,取值范围为(0, 2],
,
为[0, 1]之间均匀分布的随机数。
和
分别表示第i个粒子在t时刻的个体最优值和全局最优值。
和
分别表示为第i个粒子在t时刻的速度和位置。
3) CEEMDAN算法分解原始序列。在获取LSTM神经网络的最优参数之后,再将
经过CEEMDAN算法进行序列分解,分解后得到n个IMF
。然后,将这n个IMF各自通过公式(1)进行数据预处理,得到
,将该结果作为LSTM网络的输入。
4) LSTM网络预测。上述过程中已经得到经过PSO算法优化过后的超参数以及经过CEEMDAN算法分解后的收盘价的IMF分量。对n个IMF分别经过n个LSTM网络进行预测,得到n个预测值
,输出这n个预测结果。
5) 融合预测结果。融合函数是混合方法的核心。目前,有许多融合函数,如和、加权和、加权积等。这些融合函数的作用是将几个结果合并为最终结果。本实验的融合函数是将n个IMF各自的预测值
反归一化后进行求和。得到最终对于原始序列的预测值P,公式如式(5)和式(6)所示:
(5)
(6)
6) 评估模型。我们将最终得到的预测值与股指时间序列数据的实际值进行比较,并计算RMSE、MAE、MAPE和R2的值和记录运算时间CPU_TIME。用这五个值来评估模型的性能。它们的公式如下:
(7)
(8)
(9)
(10)
在评估模型好坏程度上,RMSE、MAE、MAPE数值越小,模型的预测结果与真实值之间的误差越小。R2越接近1代表预测值与真实值拟合度越大,模型性能越好。
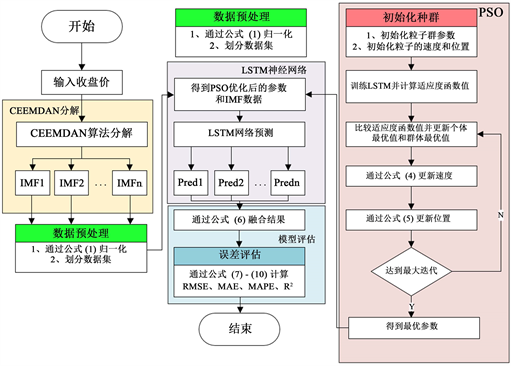
Figure 1. Price of the stock prediction process of CEEMDAN-PSO-LSTM combined model
图1. CEEMDAN-PSO-LSTM组合模型预测股票价格流程
3. 实验结果分析
本节详细介绍了本文实验部分的具体内容,为了更好的验证本文所提方法的预测结果,本次实验除了本文所提的方法之外,还与LSTM、PSO-LSTM、EMD-LSTM、CEEMDAN-LSTM这四个方法进行对比,评估的指标为RMSE、MAE、MAPE、R2和CPU_TIME。通过对比各模型的评价指标可以看出本文所提方法更加可靠。本次实验的硬件环境为CPU:12th Gen Intel(R) Core(TM)i3-12100F@3.30GHz,软件环境为window10,Python 3.8.0,TensorFlow-cpu 2.1.0。
3.1. 数据集选取
本实验的数据集来源为:https://www.tushare.pro/,表1展示了所选取数据集的名称、所属地区以及选取的时期。
本文选取了五个不同国家的各一支具有代表性的股票指数。本实验通过选取不同国家的股票指数并进行分析,旨在发现国家差异性导致的预测结果的差别。选取的五个国家分别来自亚洲的中国和日本,欧洲的德国和英国以及北美洲的美国。选取的股票指数是上证指数(SSEC)、标准普尔500指数(S&P500)、英国富时100指数(FTSE 100)、德国法兰克福指数(DAX)、日经225 (N225)。选取日期从

Table 1. The region and period of the dataset
表1. 数据集的地区和时期
2012/01/01~2024/01/01约3000天左右的各个股票指数的收盘价。本实验训练集和测试集的选取规则为前70%为训练集,后30%为测试集。随机选取数据集的10%为验证集。本文后续实验利用RMSE作为模型的损失函数,选取的epoch均为200,在整个训练周期过后保存验证集在损失函数上表现最好的那一次迭代结果作为输出。
3.2. 回看天数选择
本实验采用滚动预测建模方式,用最近look_back天的值预测下一天的值,look_back称为回看天数。但是不同股票指数利用不同回看天数进行预测的结果也不同,因此我们选取回看天数为5~10、15、20、25、30。利用本文所提模型在各数据集上进行实验,计算其MAPE,通过对比各MAPE的值,选取表现最好的回看天数。图2展示了各数据集不同回看天数选取下的MAPE的值。从图2中我们可以看到,模型在SSEC、N225、DAX、FTSE 100这四个数据集上选取回看天数为6天时预测效果最好,模型在S&P500数据集上选取回看天数为15天时预测效果最好。因此,最终本实验选取的回看天数为6天。
3.3. 模型参数设置
本文所提方法利用PSO优化LSTM层的超参数,对需要优化的超参数的取值范围设置如下:学习率大小取值范围[0.001, 0.01],批处理大小取值范围[0, 50],隐藏层单元个数取值范围[30, 300]。PSO算法涉及到的参数初始化设置如表2。本文所提方法的PSO算法部分在该初始化设置下对本文的LSTM模型的超参数进行寻优。
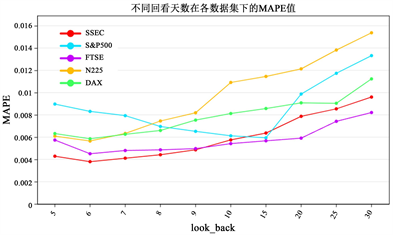
Figure 2. MAPE of different look_back for different datasets
图2. 不同回看天数在各数据集下的MAPE值

Table 2. The parameters settings of PSO algorithms
表2. PSO算法的参数设置
本实验各个网络模型的超参数设置如表3所示,其中Proposed为本文所提出的CEEMDAN-PSO-LSTM模型。本文后续实验都在表3参数设置下完成。

Table 3. The value of parameters of each method
表3. 不同方法的参数值
3.4. 实验结果及分析
本论文各方法的对比实验结果如表4所示。表中加粗部分即为表现效果最好的值,从表4中我们可以发现,本文所提方法在各个数据集上RMSE、MAE、MAPE、R2表现都优于其他模型。但是在CPU_TIME上的表现就比较差,原因是PSO算法需要时间寻找模型的最优解,并且CEEMDAN对原始序列进行分解需要时间,因此在CPU_TIME上表现最好的是最传统的LSTM模型。这在未来是可以优化的一个方向。图3和图4展示了本文所提方法在SSEC和S&P500这两个数据集上的预测结果与真实值之间的情况。从图中我们可以明显看到,所提方法在各数据集上的预测值与真实值都十分接近。这一观察结果表明我们的模型能够准确地预测目标变量,并且预测结果与真实值之间存在着密切的一致性。
通过观察表4我们可以看到对比PSO-LSTM和LSTM,经过PSO算法寻优后的LSTM模型预测精度在各个数据集都有所提高,这证明用PSO算法对LSTM超参数进行寻优是有效的。而将EMD与LSTM相结合后的模型表现对比LSTM提升就比较大,并且表现同样优于PSO-LSTM。这是因为神经网络对平缓的序列具有更好的预测效果,精度的提升很好的证明了时序分解方法与神经网络相结合的方法应用在金融预测领域效果显著。
我们还可以关注EMD-LSTM与CEEMDAN-LSTM的差别,我们可以发现CEEMDAN-LSTM表现效果都优于EMD-LSTM。这是由于CEEMDAN算法可以解决EMD算法模式混叠的问题,其分解出的IMF更适合被预测,因此与CEEMDAN-LSTM模型性能都优于与EMD-LSTM模型。但是CEEMDAN-LSTM模型在CPU-TIME上花费了更长的时间,这是因为CEEMDAN算法对比EMD算法需要更长的时间来分解原始序列,因此CEEMDAN-LSTM模型需要花费更多的运算时间。
图5展示了本实验中各个股票指数的R²雷达图。通过观察图5,我们可以清晰地看到本文所提出的方法在各个国家的股票指数上具有出色的R²值表现。这表明本文方法在不同股票指数上均展现出统一的优秀水平。我们可以特别关注到,在SSEC数据集上,本文所提出的方法相对于CEEMDAN-LSTM方法的改进并不十分显著。然而,在N225和DAX数据集上,相较于CEEMDAN-LSTM方法,本文所提出的方法展现出了明显的性能提升。这进一步证明了本文所提出的模型具有普适性,适用于预测各种类型的时间序列数据。因此,该模型非常适合用于预测各个国家的股票指数。

Table 4. Prediction results of all comparison methods for five stock indices
表4. 所有比较方法对五支股票指数的预测结果

Figure 3. The close price and prediction of SSEC of proposed algorithm
图3. 所提算法在SSEC上的收盘价的预测值和真实值
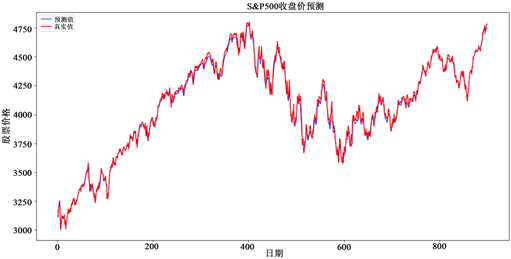
Figure 4. The close price and prediction of S&P500 of proposed algorithm
图4. 所提算法在S&P500上的收盘价的预测值和真实值
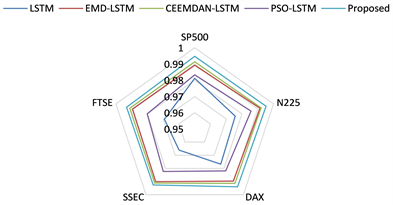
Figure 5. Radar chart of R2in this experiment
图5. 本实验关于R2的雷达图
4. 结论
在这项研究中,我们提出了一种新的神经网络模型,命名为CEEMDAN-PSO-LSTM。我们的模型将时间序列分解算法与神经网络相结合,并利用PSO算法对神经网络的超参数进行优化。通过结合时间序列分解算法,我们的模型能够有效预测具有较大波动性的序列,并通过PSO算法进一步增强模型的预测能力。在实验分析部分中我们还分析了CEEMDAN算法分解出的各个IMF分量对预测结果的影响。并且将我们的模型与其他四种深度学习方法进行了比较。我们选取了五个不同国家的数据集,使用的评估指标为RMSE、MAE、MAPE、R2以及CPU_TIME。实验结果表明,我们的方法在预测各国股票指数方面表现更佳,验证了其有效性和普适性。实验结果分析显示,结合时间序列分解方法可以更好地预测非线性和非平稳的时间序列,而结合PSO算法对LSTM网络进行优化可以减少人为调参的影响。
尽管我们提出的模型在股票预测领域提供了可行的方法,但本文的实验仍有改进的空间。首先,当预测经过时序分解方法得到的IMF1分量时,由于该序列的复杂性和随机性,模型的预测效果较差,这是我们未来需要解决的问题。其次,我们可以对基础的LSTM神经网络模型进行改进。最后,可以尝试使用其他的优化算法来优化神经网络模型的参数。
基金项目
本课题得到福建省科学技术厅面上基金科研项目(2021J011070)、福建理工大学科研启动基金资助项目(GY-Z18148)的资助。
NOTES
*通讯作者。