1. 引言
目前,辐射 + 新风空调系统广泛应用于小型办公建筑与民用建筑以提高室内舒适性。但传统的启停控制策略的主机出水温度与系统流量不稳定,会引起较大的室内空气温度波动,并且其多个设备之间未进行协同控制,会造成能源浪费。基于预测的控制策略可预测未来空调系统冷负荷并提前控制,可兼顾室内空气温度稳定与空调系统节能。基于预测的控制策略发挥作用的前提是精准的预测模型,目前应用范围最广的预测方法为人工智能方法 [1] 。在人工智能预测方法中,目前最常用的模型有支持向量机模型 [2] 、时间序列模型 [3] 、神经网络模型 [4] 等,其中神经网络预测算法无需繁冗的建模过程,且模型精度较高,相比于其他方法,它在非线性建模方面更具优势 [5] 。空调系统负荷受到室内外多方面因素影响,单一预测模型未能充分考虑负荷序列中隐含的重要信息,很难反映原始信号的变化机制,信号分解方法可以将空调负荷中的平稳信息序列与非平稳信息序列分离,从而提升预测精度 [6] 。Li等 [7] 利用小波变换法对负荷进行分解,并通过极限学习机算法(ELM)和马尔科夫蒙特卡洛方法(MABC)的混合模型分别预测负荷序列的每个分量,与传统的神经网络模型相比,该算法可以提高建模精度,减少迭代步骤。Fu等 [8] 应用经验模态分解(EMD)将原始输入信号分解为具有更好区分特征的多个子序列,并使用深度信念网络(DBN)对其分别进行特征提取和模型训练,实验结果表明,与传统预测算法相比,该方法预测精度更高。Colmenares等 [9] 提出了一种基于两种集合的风速预测方法,利用基于VMD分解的预测模型解决风速的非线性问题,提升中长期风速的预测精度。于军琪等 [10] 采用VMD算法分解空调负荷为趋势、平稳和噪声分量,并分别对三个序列进行预测重构,有效提高了负荷预测精度。
当预测精度足够后,必须建立智能控制算法,使控制变量随着负荷实时变化,从而实现按需供能。多目标优化算法可以兼顾空调系统运行过程中的多个控制目标对控制变量进行寻优,适用于复杂空调系统的精确控制。Karlsson等 [11] 以室内空气温度波动最小为优化目标,以供热量在合理范围内为约束,建立模型预测控制策略,该策略包括准确的热负荷预测模型和室内空气温度响应模型,通过二者联合优化得到最佳供水温度,模拟结果表明室内空气温度得到了更加稳定的控制。Široký等 [12] 建立了一种以能耗最低为控制目标,室内舒适度为约束的模型预测控制策略,其通过结合天气预报对未来负荷进行预测,从而控制建筑夜间混凝土的预热量,达到移峰填谷的目的,使空调系统运行费用降低,该策略中通过RC建模方法建立建筑模型。Ascione等 [13] 使用两个单目标遗传算法对控制变量执行帕累托优化,从而最大限度地降低能耗和热不适,其通过MATLAB与EnergyPlus联立对控制策略进行模拟,证明了控制策略的可行性。闫军威等人 [14] 将制冷量最大和空调系统能耗最低作为优化目标,对比多目标遗传算法与单目标粒子群算法的节能优化效果,证明多目标遗传算法在空调系统节能更具优势。
由于缺乏具体的控制方案,基于预测的辐射 + 新风系统控制策略在不同气候区的应用潜力仍不明确。本文针对辐射 + 新风空调系统低能耗与室温精确控制的需求,构建了以预测供冷量与预测负荷为约束,以MOPSO为寻优算法的控制策略。参照杭州某小型办公建筑建立辐射 + 新风空调系统模型,分别使用沈阳、北京、杭州、广州的典型年气象数据对F-MOPSO控制策略与启停控制策略进行模拟,并对F-MOPSO控制策略的节能性与室内空气温度的控制精度提升效果节能性进行探讨。
2. 方法及原理
2.1. BP神经网络算法
BP神经网络模型是一种模拟人脑神经元工作模式的人工智能模型,其具有建模简单、计算速度快、拟合精度高等优势。本文选择三层神经网络模型,结构如图1所示,Input为输入层,其神经元数量与输入参数数量相等,Hidden Layer为隐含层,其神经元数量对预测模型精度有较大影响,可通过试凑的方法获得。Output Layer为输出层,其神经元数量与输出参数数量相同。

Figure 1. Neural network model structure
图1. 神经网络模型结构
2.2. VMD算法
VMD (variational modal decomposition)采用非递归及变分模态求解模式处理原始信号,可以将具有非线性特征的空调负荷为分解为具有特定稀疏性的模态信号,且各信号分别代表空调负荷的不同特性。其分解步骤如下:
1) 将空调负荷分解为不同带宽的分量;
2) 使用希尔伯变换处理分量得到其频谱函数;
3) 将空调负荷分量的频谱通过与指数协调的方式将中心频率转移到基带;
4) 通过高斯平滑原理对变量进行带宽解调;
5) 使用二次乘法因子和拉格朗日算子将约束问题转化为无约束问题;
6) 利用乘法算子交替方向法进行解算,得到各分量和相应的中心频率。
2.3. MOPSO优化算法
MOPSO可通兼顾多个控制目标,寻优得到Pareto最优解集,解决不同控制目标的相互冲突。目标优化问题可以通过式(1)、式(2)和式(3)表示:
(1)
(2)
(3)
其中
为决策变量,
为目标函数,
和
为约束条件。
MOPSO算法速度更新和位置更新方式通过式(4)和式(5)进行更新:
(4)
(5)
其中,
为粒子位置,
为粒子速度,
为惯性权重,
和
为学习因子,
和
为
的随机数,
和
为粒子群个最优位置和全局最优位置。
预测精度评价标准
本文采用CV (Coefficient of Variation)作为评价预测精度的评价方法,具体公式如式(6)所示:
(6)
其中,
为预测值,kW;
为实际值,kW;
为平均能耗值,kW;n为数据点个数。
2.4. F-MOPSO控制策略实现流程
所提出的F-MOPSO控制策略适用于辐射 + 新风空调系统,其TRNSYS + MATLAB联合仿真模型结构如图2所示,模型建立过程如下:
1) 数据预处理:对实际监测的空调系统数据进行清洗,得到可以用于建模的数据;
2) 冷负荷预测模型与供冷量预测模型建立:选取输入参数,设定预测模型结构参数,使用VMD分解处理后的空调负荷数据,用神经网络算法分别对平稳序列及非平稳序列建模,合并各预测模型预测结果得到最终预测结果;
3) 空调系统建模:根据实际建筑与空调系统运行数据进行TRNSYS建模,并通过神经网络算法建立主机出水温度模型和除湿新风机出风温度模型,从而对TRNSYS模型中的主机出水温度和除湿新风机出

Figure 2. Structure of F-MOPSO control strategy
图2. F-MOPSO控制策略结构
风温度进行修正;
4) 多目标优化模型建立:选择目标函数,确定定值约束条件,以冷负荷预测模型与供冷量预测模型建立无约束条件,同时确定MOPSO算法粒子的位置、速度和方向更新公式;
5) 将多目标优化算法应用于空调系统控制:使用MOPSO优化模型读取辐射 + 新风空调系统模型运行数据并进行寻优,再将寻优得到的控制变量输入辐射 + 新风空调系统模型。
2.5. 系统描述
图3为TRNSYS与MATLAB联合建立的F-MOPSO控制策略仿真平台,辐射 + 新风空调系统主要构件有除湿新风机、水泵、阀门、辐射毛细管网、空调系统主机。新风除湿机将室外新风处理至低温低湿,从而承担室内湿负荷和部分显热负荷,辐射毛细管网通过辐射热交换承担部分室内显热负荷。空气源热泵作为空调系统主机制备冷水,定频水泵将冷水输送至新风除湿机组与混水三通阀,新风除湿机流量通过电动二通阀控制,辐射管网水流量通过辐射变频水泵控制。辐射管网进水温度通过混水三通阀控制辐射管网回水与主机制备的低温冷水的混合比例控制。风机为新风提供动力并通过风管将新风除湿机处理后的空气送至室内。该建筑为杭州某小型办公建筑,建筑朝向为北,面积为52 m2,房间净高为2.7 m,毛细管网敷设于建筑吊顶,室内常驻人员6名。
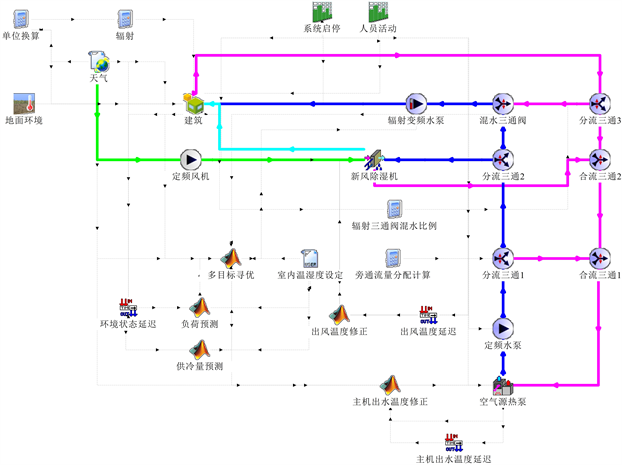
Figure 3. F-MOPSO control strategy simulation platform
图3. F-MOPSO控制策略仿真平台
空调系统能耗主要空调系统主机能耗、主机水泵能耗和辐射变频水泵能耗组成,如式(7)所示:
(7)
其中P为系统功率,kW;
为空调系统主机功率,kW;
为主机水泵功率,kW;
为辐射变频水泵功率,kW;
为了建模准确,通过数据拟合的方法对空调系统主机功率和水泵功率进行拟合,拟合公式如式(8)所示:
(8)
其中
为制冷机组提供冷量,kW;
代表室外空气干球温度,℃;
代表制冷机组出水温度,℃;
为主机水泵流量,m3;
为辐射变频水泵流量,m3
MOPSO的寻优目标之一为空调系统能耗最低,由式(8)可知当室外环境确定时,空调系统主机功率随出水温度的升高而降低,但会导致辐射变频水泵流量和新风除湿机水流量增大水泵能耗。因此确定寻优参数为空调系统主机出水温度、辐射变频水泵流量和新风除湿机水流量。
3. 预测模型建模
本文通过实际监测的杭州某小型办公建筑辐射 + 新风空调系统运行数据对预测模型及修正模型进行建模。采样时间间隔为21秒,采集了范围为6月份到7月份,数据量足够,因此首先采用拉依达准则对异常值进行处理,删除掉异常值后,再采用插值法对缺失数据进行补充。
3.1. 冷负荷预测模型
冷负荷预测模型的输入参数的合理选择对预测精度有重要影响,通过对室内外温湿度、人员活动规律、太阳辐射强度、风速等建筑冷负荷的内外影响因素进行斯皮尔曼秩相关性分析 [15] ,选择当前时刻室外空气干球温度
、室外相对湿度
、太阳水平辐射照度
、室内设备功率
、室内空气干球温度
、室内空气相对湿度
和室内目标干球温度
为输入参数。输出参数为下一时刻空调系统负荷
。当冷负荷预测模型输入参数与输出参数确定后,通过试验法确定模型隐含层神经元数量为50,确定冷负荷预测模型网络结构为6-50-1。
通过VMD算法将冷负荷数据中的平稳序列与多个非平稳序列分开,使用输入参数分别与非平稳序列和平稳序列建立BP神经网络预测模型,将各序列的预测值叠加后得到最终预测值。VMD参数设置:惩罚参数
,初始中心频率
,收敛判据
。
VMD分解数据序列时,模态数量A的选择决定了分解后的子序列是否有信息重叠,从而影响预测精度。因此对不同模态数量A进行实验,从表1可以看出,当
时,子序列的中心频率分布均匀,分解后的信息保真度较高。

Table 1. Centre frequencies corresponding to different A values
表1. 不同A值对应的中心频率
为了便于观察,截取当A = 4时的1000个冷负荷序列的分解数据点绘制出子序列分解图。从图4可以看出,每个子序列代表的信息各不相同,可作为冷负荷预测模型训练数据。
由图5所示,VMD-BP冷负荷预测模型与BP冷负荷预测模型相比更加贴近原始负荷,且通过计算可知VMD-BP模型预测结果的CV值为2.57%,相较于传统神经网络预测模型下降了13.2%,证明其可以更好的应对室内外环境变化,有效提升了负荷预测预测模型的预测精度。
3.2. 供冷量预测模型
供冷量预测模型输入参数为当前时刻室外空气干球温度
、室外相对湿度
、室内空气干球温度
、制冷机组出水温度
、辐射管网进水温度
、新风除湿机进水流量
、辐射管网进水流量
、室内目标干球温度
,输出参数为下一时刻供冷量
,神经网络模型结构为10-40-1,建立VMD-BP供冷量预测模型。如图6所示,其预测相对误差集中于−8%~6%,可满足实际工程需要。
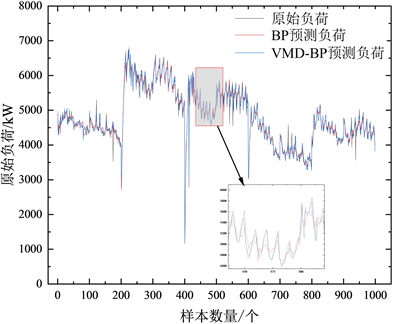
Figure 5. Comparison of prediction accuracy between VMD-BP model and BP model
图5. VMD-BP模型与BP模型预测精度对比
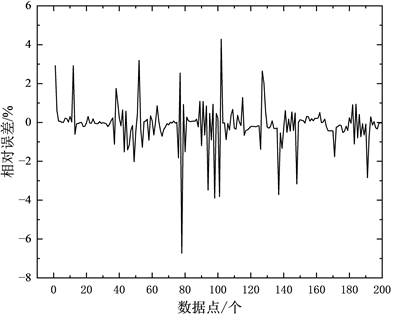
Figure 6. Prediction error of the cooling supply prediction model
图6. 供冷量预测模型预测误差
3.3. 主机出水温度与新风除湿机出水温度修正模型
如图3所示,空调系统供冷量分别由新风除湿机和辐射制冷子系统直接向室内输送,其中辐射管网参数可通过TRNBUILD进行设置。在相同工况下,制冷机组供冷量的多少体现在制冷机组出水温度的高低,新风除湿机供冷量多少体现为出风温度的高低。为了保证模拟供冷量与实际供冷量尽可能接近,本文使用BP神经网络算法分别对制冷机组出水温度和新风除湿机出风温度进行建模。
考虑控制延迟的影响,空调系统主机出水温度神经网络模型输入参数选用:控制时刻制冷机组设定出水温度、制冷机组的启停信号、制冷机组进水温度、室外空气温湿度和上一时刻制冷机组出水温度。图7显示在相同输入参数条件下,模拟出水温度与实际温度接近,BP神经网络模型可有效修正空调系统主机出水温度。
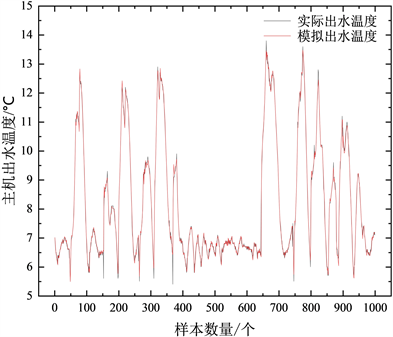
Figure 7. Comparison of simulated main unit water temperature and actual water temperature
图7. 主机模拟出水温度与实际出水温度对比

Figure 8. Comparison of simulated and actual dehumidifier air temperature
图8. 新风除湿机模拟出风温度与实际出风温度对比
同样考虑控制延迟的影响,新风除湿机出风温度神经网络模型的输入参数设定为:控制时刻流经新风除湿机的水流量、新风除湿机进水温度、进入新风除湿机的空气温湿度和上一时刻新风除湿机出风温度。图8显示在相同输入参数条件下,模拟出水温度与实际温度接近,BP神经网络模型可有效修正新风除湿机出风温度。
4. 控制策略对比试验
MOPSO算法通过调用MATLAB实现,其目标函数设定为能耗最低与室内空气温度接近设定值,约束条件为预测供冷量与预测负荷差值小于10W、新风除湿机阀门开度在0%~100%、辐射变频水泵运转频率介于60%~100%和主机出水温度介于7℃~15℃。MOPSO初始参数设置情况为:初始粒子数
,最大迭代数
,精英库容量
,惯性权重
,学习因子
,学习因子
,粒子最大搜索速度
,变异率
。
为了进行后续的节能分析,需要对不同地区进行控制测策略实验。如图9所示,沈阳、北京、杭州、广州的室外干球温度分别在6月10日~8月、5月20日~9月、6~9月、5~10月超过26度,其制冷季长度不同,因此需要分别对四个城市的节能总量进行计算。
 (a) 沈阳 (b) 北京
(a) 沈阳 (b) 北京 (c) 杭州(d) 广州
(c) 杭州(d) 广州
Figure 9. Outdoor ambient temperature in different cities
图9. 不同城市室外环境温度
图10为选取空调系统单日平均负荷率为80%时室内空气温度与主机出水温度变化情况,由图可知采用F-MOPSO控制策略相较于启停控制策略的室内空气温度更加平稳,主机出水温度可根据冷负荷按需变化,防止温度过低,造成主机能耗增加并造成空调系统的过度制冷。

Figure 10. Indoor air temperature and main engine water temperature at 80 per cent average load rate in a single day
图10. 单日平均负荷率为80%时室内空气温度和主机出水温度
由图11可知四个城市F-MOPSO控制策略下的空调系统的冷负荷相较于启停控制策略均有所降低,参照图10可知这是由于优化后的室内空气温度相较于优化前低于26℃的时间段更少,降低了空调系统的过度制冷量造成的。

Figure 11. Air conditioning cooling load under F-MOPSO control strategy and start-stop control strategy
图11. F-MOPSO控制策略与启停控制策略下的空调系统冷负荷
由图12可知,四个城市采用F-MOPSO策略相较于启停控制策略的空调系统能耗均有所降低,但其节能比例随着地理位置由北向南逐渐变小,这是室外温度随着地理位置向南逐渐升高,空调系统冷负荷增大,节能空间变小造成的。但由于广州的制冷季更长,广州节能量相较于其他三个城市反而更高,为643 kW∙h。

Figure 12. Power consumption of air conditioning system under F-MOPSO control strategy and start-stop control strategy
图12. F-MOPSO控制策略与启停控制策略下的空调系统功耗
5. 结论
1) 采用VMD算法与BP神经网络算法联合构建的预测模型与传统BP神经网络算法构建的预测模型相比,预测精度更高,更适合实际工程的应用,为辐射 + 新风空调系统进行准确预测控制提供基础。
2) F-MOPSO控制策略与启停控制策略相比,其在控制过程中能够保证室内空气温度与设定温偏离度更小,辐射 + 新风空调系统的过度制冷量减少,整个系统功耗更低。
3) F-MOPSO控制策略应用在沈阳、北京、杭州与广州均可达到节能效果,其中在广州的节能效果最好,相较于启停控制策略可以达到643 kW∙h。