DOI: 10.12677/PM.2024.141034, PDF, HTML, XML,  被引量    国家自然科学基金支持
作者: 杜 珺：内蒙古师范大学数学科学学院，内蒙古 呼和浩特；黄月梅^*：内蒙古师范大学数学科学学院，内蒙古 呼和浩特；内蒙古自治区应用数学中心，内蒙古 呼和浩特
关键词: 半循环可分组设计；循环差阵；循环填充；递归构造；Semi-Cyclic Group Divisible Design； Cyclic Difference Matrix； Cyclic Packing； Recursive Construction

文章引用：杜珺, 黄月梅. 型为t ^r的5-半循环可分组设计[J]. 理论数学, 2024, 14(1): 335-340. https://doi.org/10.12677/PM.2024.141034

1. 引言

设 $r,t$ 和k都是正整数， $I_r=\left\{0,1,2,\cdots ,r-1\right\}$ 且 $Z_t$ 表示模t剩余类加群。令 ${\mathcal{B}}^{*}$ 是点集 $X=I_r\times Z_t$ 的k元子集族(基区组集)。对 $I_r$ 中任意两个整数x和y及 ${\mathcal{B}}^{*}$ 中的k-子集B定义

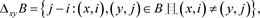
则 ${\Delta }_{xy}{\mathcal{B}}^{*}=\underset{B\in {\mathcal{B}}^{*}}{\cup }{\Delta }_{xy}B$ ，其中减法模t计算。 ${\Delta }_{xy}{\mathcal{B}}^{*}$ 中的差称为 ${\mathcal{B}}^{*}$ 的 $\left(x,y\right)$ 差。若当 $x\ne y$ 时， ${\Delta }_{xy}{\mathcal{B}}^{*}=Z_t$ ，

否则 ${\Delta }_{xy}{\mathcal{B}}^{*}=\varnothing$ ，则称 $\left(X,\mathcal{G},{\mathcal{B}}^{*}\right)$ 是 $X=I_r\times Z_t$ 上，组集为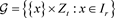的一个型为t^r的半循环可分组设计(semi-cyclic group divisible design)，简记为k-SCGDD。

例1 令 $X=I_5\times Z_7$ ， $\mathcal{G}=\left\{\left\{x\right\}\times Z_7:x\in I_5\right\}$ ，则下列7个区组构成型为7⁵的5-SCGDD的基区组：

$\left\{\left(0,0\right),\left(1,0\right),\left(2,0\right),\left(3,0\right),\left(4,0\right)\right\}$ , $\left\{\left(0,1\right),\left(1,2\right),\left(2,3\right),\left(3,4\right),\left(4,0\right)\right\}$ ,

$\left\{\left(0,2\right),\left(1,4\right),\left(2,6\right),\left(3,1\right),\left(4,0\right)\right\}$ , $\left\{\left(0,3\right),\left(1,6\right),\left(2,2\right),\left(3,5\right),\left(4,0\right)\right\}$ ,

$\left\{\left(0,4\right),\left(1,1\right),\left(2,5\right),\left(3,2\right),\left(4,0\right)\right\}$ , $\left\{\left(0,5\right),\left(1,3\right),\left(2,1\right),\left(3,6\right),\left(4,0\right)\right\}$ ,

$\left\{\left(0,6\right),\left(1,5\right),\left(2,4\right),\left(3,3\right),\left(4,0\right)\right\}$ ,

通过对以上七个基区组的每个元素的第二分量加1并模7运算就可以得到型为7⁵的5-SCGDD的所有区组。

半循环可分组设计的定义由Yin J. [1] 提出。半循环可分组设计在其它设计和光正交码的构造中有重要的应用，因此它的存在性和组合构造问题被进行了系统地研究。Gallant R. P.等 [2] 解决了3-SCGDD存在的充要条件。Wang J. [3] 和Wang K. [4] 等给出型为 $m^n$ 的k-SCGDD的递归构造方法，并解决了4-SCGDD

的存在问题。近期，Wang L.等 [5] 给出当p为奇素数，t为正整数时，型为 ${\left(p^r\right)}^{{\left(\frac{p+1}{2}\right)}^t}$ 的 $\frac{p+1}{2}$ -SCGDD的存在条件。

目前关于5-SCGDD还没有独立的研究结果，因此本文对5-SCGDD的存在谱和构造问题进行了研究。首先从半循环可分组设计的定义出发，给出了型为t^r的5-SCGDD存在的必要条件，再借助循环差阵和t-正则循环填充设计及递归构造方法得到了型为t^r的5-SCGDD存在的部分充分条件，所得结果丰富了半循环可分组设计的研究内容。

2. 辅助设计及构造方法

半循环可分组设计的结构与循环差阵、循环填充及平衡不完全区组设计等设计有密切联系，下面给出相关设计的定义。

设 $k,t$ 是正整数。一个循环差阵(CDM)是一个 $k\times t$ 阶矩阵 $A=\left(a_{ij}\right)$ ， $a_{ij}\in Z_t$ ，且任意两行都满足 $\left\{a_{mj}-a_{nj}\left(\mathrm{mod}t\right):0\le j\le t-1\right\}=Z_t$ ，其中 $0\le m$ ， $n\le k-1$ ， $m\ne n$ ，记作 $\left(k,t\right)$ -CDM。

令 $v=rt$ ， $X=Z_{rt}$ ， $\mathcal{A}$ 是X的s个k元子集(基区组)的集合。若 $\Delta \mathcal{A}=\left\{b-a\left(\mathrm{mod}v\right):A_i\in \mathcal{A},a,b\in A_i,a\ne b,1\le i\le s\right\}$ 包含 $Z_{rt}$ 中的每个非零元至多一次，则 $\left(X,\mathcal{A}\right)$ 称为一个循环填充设计，记作CP $\left(k,1;rt\right)$ 。特别地，若 $Z_{rt}\backslash \Delta \mathcal{A}$ 可构成 $Z_{rt}$ 的一个阶为t的加法子群，则CP $\left(k,1;rt\right)$ 又记作t-正则CP $\left(k,1;rt\right)$ 。在文献 [6] 中，t-正则CP $\left(k,1;v\right)$ 也被称作差族，简记为 $\left(v,t,k,1\right)$ -DF。

设 $v,k,\lambda$ 是正整数。一个平衡不完全区组设计，记作BIBD $\left(k,\lambda ;v\right)$ (或B $\left(k,\lambda ;v\right)$ )，是一个二元组 $\left(X,\mathcal{B}\right)$ ，需满足条件：1) $\left|X\right|=v$ ；2) 对任意的 $B\in \mathcal{B}$ ，都有 $\left|B\right|=k$ ；3) X中任意两个不同的元素都恰好包含在λ个区组B中。

半循环可分组设计与以上几个设计之间的关系有如下几个结论。

引理1 [3] 型为t^k的k-SCGDD与 $\left(k,t\right)$ -CDM等价。

引理2 [3] 若t-正则CP $\left(k,1;rt\right)$ 存在，则存在型为t^r的k-SCGDD。

以下是与半循环可分组设计有关的两个递归构造法。

构造法1 [3] 若型为t^r和型为m^k的k-SCGDD都存在，则存在型为 ${\left(tm\right)}^r$ 的k-SCGDD。

构造法2 [3] 若B $\left(k,1;v\right)$ 和型为t^k的k-SCGDD存在，则存在型为t^v的k-SCGDD。

以上两种构造方法具有一定的普适性，有助于我们得到更多类型的半循环可分组设计。

文献 [7] - [13] 中给出关于B $\left(\text{5},\text{1};v\right)$ 、 $\left(5,t\right)$ -CDM和t-正则CP $\left(5,1;rt\right)$ 的存在条件如下：

引理3 [7] 当 $v\equiv 1,5\left(\mathrm{mod}20\right)$ 且 $v\ge 5$ 时，B $\left(\text{5},\text{1};v\right)$ 存在。

引理4 [8] 当t是奇数， $t\ne 3$ 且 $\gcd \left(t,27\right)\ne 9$ 时， $\left(5,t\right)$ -CDM存在；当 $t=9p$ ， $p\in \left\{3,5,7,9,11,13,17,19,23,27,29,31,109\right\}$ 时， $\left(5,t\right)$ -CDM也存在。

引理5 [9] 当 $k\ge 3$ ，t为偶数时， $\left(k,t\right)$ -CDM不存在； $\left(4,9\right)$ -CDM也不存在。

推论1 $\left(5,9\right)$ -CDM不存在。

证明：设A是一个 $\left(k,t\right)$ -CDM。由循环差阵的定义，移除A 任意一行得到一个 $\left(k-1,t\right)$ -CDM；因此，若 $\left(k-1,t\right)$ -CDM不存在，则 $\left(k,t\right)$ -CDM也不存在。由引理5可知， $\left(4,9\right)$ -CDM不存在，故 $\left(5,9\right)$ -CDM也不存在。

引理6 [10] [11] [12] [13] 设 $t,r$ 是正整数，则对下列参数，t-正则CP $\left(5,1;rt\right)$ 存在：

1) 当 $t=5,15$ 或45， $r\equiv 1\left(\mathrm{mod}4\right)$ 是素数且 $r>5$ ；

2)当 $\left(t,r\right)\in \{\left(2,41\right),\left(2,61\right),\left(3,41\right),\left(3,61\right),\left(5,25\right),\left(8,16\right),\left(10,9\right),\left(10,13\right),\left(10,17\right),\left(12,16\right),\left(15,9\right),\left(20,11\right),$ $\left(25,9\right)\}$ ；

3) 当 $t=4$ 或20， $r\equiv 1\left(\mathrm{mod}10\right)$ 是素数且 $r\ne 11$ ；

4) 当 $t=8$ 或12， $r\equiv 11\left(\mathrm{mod}20\right)$ 是素数；

5) 当 $t=60$ ，r是素数且 $r>5$ 。

下面给出利用循环差阵、t-正则循环填充以及递归构造法构造半循环可分组设计的具体例子。

例2 型为5⁵的5-SCGDD存在。

证：一个(5,5)-CDM如矩阵A所示：

$A=\left[\begin{array}{ccccc}0& 2& 4& 3& 1\\ 0& 4& 3& 1& 2\\ 0& 3& 1& 2& 4\\ 0& 1& 2& 4& 3\\ 0& 0& 0& 0& 0\end{array}\right]$ .

可以验证，当 $0\le m$ ， $n\le 4$ ， $m\ne n$ 时，任意两行都满足 $\left\{a_{mj}-a_{nj}\left(\mathrm{mod}5\right):0\le j\le 4\right\}=Z_5$ ，符合循环差阵的定义。令 $I_5=\left\{0,1,2,3,4\right\}$ ， $B_j=\left\{\left(0,a_{0j}\right),\left(1,a_{1j}\right),\left(2,a_{2j}\right),\left(3,a_{3j}\right),\left(4,a_{4j}\right)\right\}$ ，其中 $j=0,1,2,3,4$ ，则 ${\mathcal{B}}^{*}=\left\{B_0,B_1,B_2,B_3,B_4\right\}$ 构成点集 $X=I_5\times Z_5$ 上，组集为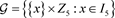的型为5⁵的5-SCGDD的基区组集。

例3 若存在10-正则CP $\left(5,1;9\times 10\right)$ ，则存在型为10⁹的5-SCGDD。

证明：文献 [10] 给出一个10-正则CP $\left(5,1;9\times 10\right)$ 的基区组集 $\mathcal{A}=\left\{A_1,A_2,A_3,A_4\right\}$ ，其中四个区组为 $A_1=\left\{0,1,3,8,58\right\}$ ， $A_2=\left\{0,4,21,51,70\right\}$ ， $A_3=\left\{0,6,16,29,44\right\}$ ， $A_4=\left\{0,11,25,37,59\right\}$ 。

对于任意的 $A=\left\{a_1,a_2,a_3,a_4,a_5\right\}\in \mathcal{A}$ ，令 $a_l=m_l+9n_l$ ， $0\le m_l\le 8$ ， $1\le l\le 5$ ，则得到对应的二元组 $B_A=\left\{\left(m_1,n_1\right),\left(m_2,n_2\right),\left(m_3,n_3\right),\left(m_4,n_4\right),\left(m_5,n_5\right)\right\}$ 。定义 $A^j=\left\{a_1+j,a_2+j,a_3+j,a_4+j,a_5+j\right\}$ 为A的平移，

$j=0,1,\cdots ,8$ 。对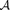的四个区组及它们的平移做上述转换，则 $\mathcal{B}=\left\{B_{A_i^j}|i=1,2,3,4;j=0,1,\cdots ,8\right\}$ 构成点集

$X=I_9\times Z_{10}$ 上，组集为 $\mathcal{G}=\left\{\left\{x\right\}\times Z_{10}:x\in I_9\right\}$ 的型为10⁹的5-SCGDD的基区组集。

例4 若型为7⁵和型为5⁵的5-SCGDD都存在，则型为35⁵的5-SCGDD也存在。

证明：设型为7⁵的5-SCGDD的点集 $X=I_5\times Z_7$ ，组集 $\mathcal{G}=\left\{\left\{x\right\}\times Z_7:x\in I_5\right\}$ ，基区组集 ${\mathcal{B}}^{*}=\left\{B_i|i=1,\cdots ,7\right\}$ 。对任意 $B=\left\{\left(a_0,b_0\right),\left(a_1,b_1\right),\left(a_2,b_2\right),\left(a_3,b_3\right),\left(a_4,b_4\right)\right\}\in {\mathcal{B}}^{*}$ ，由例2，存在点集 $I_5\times Z_5$ 上，组集为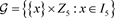，基区组集 ${\mathcal{C}}^{*}=\left\{C_i|i=1,\cdots ,5\right\}$ 的型为5⁵的5-SCGDD。利用构造1，对任意的 $C\in {\mathcal{C}}^{*}$ ， $C=\left\{\left(c_0,d_0\right),\left(c_1,d_1\right),\left(c_2,d_2\right),\left(c_3,d_3\right),\left(c_4,d_4\right)\right\}$ ，做

$D_B=\left\{\left(a_{c_0},b_{c_0}+7d_0\right),\left(a_{c_1},b_{c_1}+7d_1\right),\left(a_{c_2},b_{c_2}+7d_2\right),\left(a_{c_3},b_{c_3}+7d_3\right),\left(a_{c_4},b_{c_4}+7d_4\right)\right\}$ .

再令 ${\mathcal{D}}_B$ 表示这些 $D_B$ 构成的集合，其中 $\left\{\left(c_0,d_0\right),\left(c_1,d_1\right),\left(c_2,d_2\right),\left(c_3,d_3\right),\left(c_4,d_4\right)\right\}$ 取遍 ${\mathcal{C}}^{*}$ 中的5个基区组，则 ${\mathcal{D}}^{*}={\displaystyle {\cup }_{B\in {\mathcal{B}}^{*}}{\mathcal{D}}_B}$ 构成点集 $X=I_5\times Z_{35}$ 上，组集的型为35⁵的5-SCGDD的基区组集。

3. 型为t^r的5-SCGDD的存在条件

这一小节将讨论型为t^r的5-SCGDD的存在条件。

定理1 型为t^r的5-SCGDD存在的必要条件是 $r\ge 5$ ， $\left(r-1\right)t\equiv 0\left(\mathrm{mod}4\right)$ 且 $r\left(r-1\right)t\equiv 0\left(\mathrm{mod}20\right)$ 。

证明：设 $\left(X,\mathcal{G},{\mathcal{B}}^{*}\right)$ 是一个型为t^r的5-SCGDD。由可分组设计的定义，区组中的每个点取自不同的组，故 $r\ge 5$ ；而包含点集中任意一个点x的区组个数为 $r_x=\frac{t\left(r-1\right)}{4}$ ，又 $r_x$ 为正整数，所以 $\left(r-1\right)t\equiv 0\left(\mathrm{mod}4\right)$ 。因为共有rt个点，所有的区组个数为 $b=\frac{t^{2}r\left(r-1\right)}{20}$ ，而每个区组轨道的长为t，所以基区组的个数为 $b^{\ast }=\frac{tr\left(r-1\right)}{20}$ ，因此 $r\left(r-1\right)t\equiv 0\left(\mathrm{mod}20\right)$ 。

定理2 若t是奇数且 $t\ne 3,9$ 或9p，其中p是素数， $p\ge 37$ 且 $p\ne 109$ 时，型为t⁵的5-SCGDD存在。当 $t\in \left\{3,9\right\}$ 或为偶数时，型为t⁵的5-SCGDD不存在。

证明：当 $t=3$ 时， $\left(5,3\right)$ -CDM不存在，由引理1，型为3⁵的5-SCGDD不存在；由引理1、5和推论1，当 $t=9$ 或t是偶数时，型为t⁵的5-SCGDD不存在；当t是奇数且 $\gcd \left(t,27\right)\ne 9$ 以及 $t=9p$ ，p为素数， $3\le p\le 31$ 或 $p=109$ 时，由引理1、4可知，型为t⁵的5-SCGDD存在。下面只需考虑 $t=9p_1{p}_2\cdots p_m$ ， $m\ge 2$ ，其中 $p_i\ge 5$ ， $1\le i\le m$ 是素数的情况。由引理1、4，存在型为 ${\left(3p_1\right)}^5$ 的5-SCGDD和型为 ${\left(3p_2{p}_3\cdots p_m\right)}^5$ 的5-SCGDD，再由构造法1，型为 ${\left(9p_1{p}_2\cdots p_m\right)}^5$ 的5-SCGDD存在。综上，结论得证。

定理3 当t为奇数， $t\ne 3,9$ 或9p， $p\ge 37$ 为素数且 $p\ne 109$ ， $r\equiv 1,5\left(\mathrm{mod}20\right)$ ， $r>5$ 时，型为t^r的5-SCGDD存在。

证明：由引理3，当 $r\equiv 1,5\left(\mathrm{mod}20\right)$ 且 $r\ge 5$ 时，B $\left(5,1;r\right)$ 存在；又由定理2，当t是奇数， $t\ne 3,9$ 或9p， $p\ge 37$ 是素数且 $p\ne 109$ 时，型为t⁵的5-SCGDD存在；再利用构造法2，结论得证。

由引理2、6及定理3易得下面结论。

推论2 当 $t,r$ 满足下列条件之一时，型为t^r的5-SCGDD存在：

1) $\left(t,r\right)\in \left\{\left(3,41\right),\left(3,61\right),\left(15,9\right),\left(25,9\right)\right\}$ ；

2) $t=5,15$ 或45， $r\equiv 9,13,17\left(\mathrm{mod}20\right)$ 是素数。

推论3 当 $m,q$ 为奇数， $m,q\ne 3,9$ 或9p， $p\ge 37$ 为素数且 $p\ne 109$ ，t和r取值为以下情况时，型为 ${\left(tm\right)}^r$ 的5-SCGDD存在：

1) $t=2$ ， $r=41,61$ 且 $m\ne 5q$ ；

2) $t=4$ ， $r\equiv 1\left(\mathrm{mod}10\right)$ 是素数且 $r\ne 11$ ， $m\ne 5q$ ；

3) $t=8$ ， $r\equiv 11\left(\mathrm{mod}20\right)$ 是素数或 $r=16$ ；

4) $t=10$ ， $r=9,13,17,41,61$ ；

5) $t=12$ ， $r\equiv 11\left(\mathrm{mod}20\right)$ 是素数或 $r=16$ ， $m\ne \frac{1}{3}q,\frac{5}{3}q$ 和5q；

6) $t=20$ ， $r\equiv 1\left(\mathrm{mod}10\right)$ 是素数， $m\ne 3q$ ；

7) $t=60$ ， $r>5$ 是素数。

证明：利用构造法1，结合引理2、6和定理2，结论得证。

4. 小结

本文先确定了型为t^r的区组长度为5的半循环可分组设计存在的必要条件，再根据已知的辅助设计，如循环差阵，t-正则循环填充的部分存在条件及两个递归构造方法，给出型为t^r的5-SCGDD存在的若干充分条件，即得到了此半循环可分组设计的无穷类，所得结果对半循环可分组设计及带有AM-OPPTS/PW限制的光正交码的研究工作有一定的理论参考价值。

基金项目

国家自然科学基金青年基金项目(11401326)；无穷维哈密顿系统及其算法应用教育部重点实验室开放课题(2023KFZR03)；内蒙古自治区高等学校科学研究项目(NJZY19021，NJZY22599，NJZY22600)。

NOTES

^*通讯作者。

参考文献

[1]	Yin, J.X. (2002) A General Construction for Optimal Cyclic Packing Designs. Journal of Combinatorial Theory (Series A), 97, 272-284. https://doi.org/10.1006/jcta.2001.3215
[2]	Gallant, R.P., Jiang, Z. and Ling, A.C.H. (1999) The Spectrum of Cyclic Group Divisible Designs with Block Size Three. Journal of Combinatorial Design, 7, 95-105. https://doi.org/10.1002/(SICI)1520-6610(1999)7:2%3C95::AID-JCD2%3E3.0.CO;2-K
[3]	Wang, J.M. and Yin, J.X. (2010) Two-Dimensional Optical Orthogonal Codes and Semicyclic Group Divisible Designs. IEEE Transactions on Information Theory, 56, 2177-2187. https://doi.org/10.1109/TIT.2010.2043772
[4]	Wang, K. and Wang, J.M. (2012) Semicyclic 4-GDDs and Related Two-Dimensional Optical Orthogonal Codes. Designs, Codes and Cryptog-raphy, 63, 305-319. https://doi.org/10.1007/s10623-011-9556-3
[5]	Wang, L.D., Feng, T., Li, Y.T., et al. (2023) Construction for Multichannel Conflict-Avoiding Codes with AM-OPPTS Restriction. IEEE Transactions on Infor-mation Theory, 69, 7398-7413. https://doi.org/10.1109/TIT.2023.3299307
[6]	Ge, G.N. and Yin, J.X. (2001) Constructions for Optimal Optical Orthogonal Codes. IEEE Transactions on Information Theory, 47, 2998-3004. https://doi.org/10.1109/18.959278
[7]	Hanani, H. (1975) Balanced Incomplete Block Designs and Related Designs. Discrete Mathematics, 11, 255-369. https://doi.org/10.1016/0012-365X(75)90040-0
[8]	Pan, R., Abel, R.J.R., Bunjamin, Y.A., et al. (2022) Differ-ence Matrices with Five Rows over Finite Abelian Groups. Designs, Codes and Cryptography, 90, 367-386. https://doi.org/10.1007/s10623-021-00981-6
[9]	Ge, G.N. (2005) On -Difference Matrices. Discrete Mathematics, 301, 164-174. https://doi.org/10.1016/j.disc.2005.07.004
[10]	Yin, J.X. (1998) Some Combinatorial Constructions for Optical Orthogonal Codes. Discrete Mathematics, 185, 201-219. https://doi.org/10.1016/S0012-365X(97)00172-6
[11]	Chang, Y.X. and Ji, L.J. (2004) Optimal Opti-cal Orthogonal Codes. Journal of Combinatorial Designs, 12, 346-361. https://doi.org/10.1002/jcd.20011
[12]	Ma, S. and Chang, Y.X. (2004) A New Class of Optimal Optical Orthogonal Codes with Weight Five. IEEE Transactions on Information Theory, 50, 1848-1850. https://doi.org/10.1109/TIT.2004.831845
[13]	Ma, S. and Chang, Y.X. (2005) Constructions of Optimal Optical Orthogonal Codes with Weight Five. Journal of Combinatorial Designs, 13, 54-69. https://doi.org/10.1002/jcd.20022