1. 概述
铁机辆〔2020〕90号文中定义车轮多边形是指车轮表面沿圆周方向出现的周期性磨损。车轮多边形是车轮不圆顺的一种特殊表现形式,并规定1~13阶称为低阶多边形,14阶及以上称为高阶多边形。机车车辆领域中,轮对作为车辆的载重部件,车轮若存在多边形会产生周期的轮轨作用力,并引起轮轨及车辆减振部件受力激增,给行车安全带来重大隐患。车轮多边形目前已是动车运维及日常检修重要指标,在机车车辆日常安全检测中也为必不可少,如何准确快速的检测出不圆度超限车轮,做到车轮多边形及时报警检修,关系着车辆行车安全和运营效率 [1] 。
目前对于车轮多边形检测的方法主要包括顶转轮测量、车载检测、轨边检测三种类型 [2] 。顶转轮测量如德国BBM高精度多边形测量设备为静态测量,对转动平台要求高,对车轮监测频率低;车载间接地测量多边形产生的轮轨振动,准确性不高且安装量大。轨边非接触式检测,如德国DB、澳大利亚TrackIQ研制的系统,目前已进入国产化阶段(铁科院TPDS)。同车载一样为间接测量,要求较高的过车时速,且振动干扰大 [3] [4] 。
如在一级修检测棚的擦伤检测设备上实现多边形接触式检测,则可进行多边形日常监测,能保证多边形检出的及时性及准确性,且检出后能立即回库进行检修。
2. 检测原理介绍
其基本原理是:通过测量车轮轮缘下垂量的变化,实现对踏面擦伤及磨损的测量,以此来确定车轮的不圆度。如图1所示,车轮踏面受损后,其圆周的半径将减小Δh,也就使得轮缘顶点相对于钢轨的位置将下降Δh。上述变化信息包含了车轮踏面不圆度的信息。
如图2所示,接触式测量法使用检测杆来测量轮缘顶点所在圆周(假设半径为R)与踏面滚动圆圆周(假设半径为r)的高度差,会产生如图3所示的U字形波形,U字形波形的高度h = R − r。而当踏面存在不圆时,检测杆高度变化量Δh则反应了踏面的起伏当量,如图4所示为U字形波形底部放大,可看出单个车轮经过单个杆的局部起伏Δh及对应当量(纵坐标单位mm)。
图4为车轮存在多边形的U字底部局部放大波形。根据不圆度的定义(不圆度可以定义为滚动圆处,最大半径和最小半径差:maxΔh),不圆度(包括多边形)只与图4的局部起伏有关,故检测分析只使用U字形波形底部。

Figure 1. Schematic diagram of the vertical height change of the wheel when the wheel is not round
图1. 车轮不圆下车轮的垂向高度变化示意图

Figure 2. Principle of wheel out-of-roundness detection
图2. 车轮不圆度检测原理

Figure 3. Original waveform of a single detection rod
图3. 单根检测杆的原始波形
“轮对不圆度动态检测系统”安装在整体道床上,如图5所示,按照过车方向,钢轨内侧分别有8个检测杆,其中过车方向右侧为CS1、CS2、CS3、CS4四根检测杆,左侧由CS5、CS6、CS7、CS8四根检测杆。通过单侧4根杆的U字形底部段拼接,即可得到一个车轮整圈的起伏波形。

Figure 4. Polygonal waveform of a single detection rod
图4. 单根检测杆的多边形波形

Figure 5. Contact measurement method detection rod layout diagram
图5. 接触式测量法检测杆布局图
3. 谱减算法的改进
谱减算法(Spectral Subtraction)是最早出现的语音增强算法之一,由于实现简单且实时性较好,获得了广泛的应用。它假设语音和噪声是加性混合,且噪声是缓慢变化的,通过在静音段估计和更新噪声频谱,从带噪语音谱中减去噪声来增强语音 [5] [6] 。
假设估计的噪声的幅度谱为
,则降噪后的语音信号谱可以表示为:
(1)
其中,
为降噪后信号,
为原始信号,
为信号相位角。
信号的幅度谱总是非负的,因此要做一下保护,即:
(2)
上述为传统的幅度谱减算法,当处理接触式擦伤波形时,如图4可知下压波形除了车轮多边形导致的局部起伏波形外,还存在低频起伏偏差,该低频起伏偏差由钢轨上表面不平顺磨耗、擦伤杆机械安装轻微偏斜等非车轮因素导致。此外,擦伤波形还存在机车高压部件电干扰等。使用谱减算法是为了滤除上述干扰成分,而传统的幅度谱减算法中对噪声进行估计再相减的方式,只能估计出电干扰一类与擦伤起伏波形差异及统计特征偏差大的噪声,故不太适用于上述擦伤波形存在的干扰滤除场景。
针对擦伤波形干扰特征,如除高频电干扰毛刺等,钢轨磨耗起伏及擦伤杆机械安装轻微偏斜导致的低频起伏波形,理论上在每个车轮的U字形下压波形中均固定不变。特针对此特征进行算法改进设计,将估计的噪声的幅度谱
替换为所有车轮下压波形的幅度谱的中值幅度谱,中值幅度谱即每个
对应的幅度为单侧所有车轮在该
对应的所有幅度的均值组成的中值幅度谱(如式3所示),最后同公式1及公式2计算每个车轮幅度谱分别减去所有车轮计算的中值幅度谱,实现改进的幅度谱减算法。此方法即可滤除频率成分相同的电噪声,也可滤除同一个擦伤杆所有轮波形中起伏相同的钢轨磨耗及安装偏差,以实现高精度检测。
(3)
其中,
为改进算法中噪声估计,即为中值幅度谱,
为同一根杆所有车轮的幅度谱,wheel为车轮序号。
如图6所示为一例多边形车轮案例的原始单杆波形滤波前后对比。图6(a)的原始波形中含明显毛刺电噪声及低频起伏噪声,无法分辨是否含有多边形成分,容易造成车轮多边形漏报。经过本文改进谱减算法滤波后,如图6(b)所示,得到干净的多边形波形。
4. 多边形粗糙度计算
参考标准ISO 3095:2005,也是国内动车及机辆车轮不圆度指标运用的公式 [7] :
车轮粗糙度水平
定义如公式(4),单位为dB re 1 μm
(4)
式中,
是车轮不圆度波形转频域后在1/3倍频程k中进行量化的值。
为车轮粗糙度的参考值(1 μm不圆度波形转频域后在1/3倍频程k中进行量化的值)。在国际标准单位下频带中心波长为:
(5)
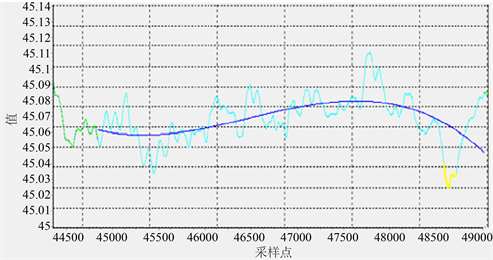 (a) 原始波形
(a) 原始波形 (b) 改进谱减算法滤波后
(b) 改进谱减算法滤波后
Figure 6. Original single-pole polygon wheel waveform before and after filtering
图6. 原始单杆多边形车轮波形滤波前后
在每个1/3倍频程中将所得的窄带频谱幅值的平方再求和,并除以计算点数即可获得
。
图7为一例19阶多边形波形在极坐标下的展示。经过上述公式计算得到图8粗糙度谱,其中横坐标为多边形阶次,纵坐标为粗糙度幅值,单位dB。可看出19阶处有明显超限波峰,表明该车轮存在19阶多边形。

Figure 8. Roughness spectrum-peak at 19th order
图8. 粗糙度谱-峰值在19阶
5. 结论
轮轨关系一直是国内外学者关注的热门话题,而如何实现定量的检测车轮多边形,是铁路安全检测的重要课题。本文以接触式测量法的擦伤检测系统数据为研究对象,开展多边形检测的深入研究,特别是针对擦伤工况的干扰问题,如电噪声、钢轨不平顺及擦伤杆与钢轨不平行等带来的干扰,导致无法分辨是否含有多边形成分。基于干扰特性,结合多个车轮波形,提出了谱减算法的改进方法。
经上百趟过车数据验证,有较好的效果,多边形实车轮检测波形使用此改进滤波后能得到干净的多边形波形并准确检出(本文中均为实车波形),表明本文方法提高了实际运用中多边形检测的准确性及当量精度。本文算法无论对接触式擦伤系统或对于其他技术路线的多边形检测系统,在提高检测车轮多边形当量及报警准确率上均具有较好的参考作用。
基金项目
兰州局集团公司科技研究开发计划课题(LZJKY2023009-2)。

