1. 前言
油气生成和泥炭成煤的过程是发生在沉积盆地里重要的生物化学和物理化学反应过程,也称之为有机质的变质、演化和成熟。在这漫长过程中,温度和时间是两个最为重要的反应参数,而镜质体反射率则是客观衡量反应速率和进展程度的重要标识 [1] [2] [3] [4] [5] 。镜质体反射率在沉积有机质变质、演化和成熟过程中对温度和时间的影响效应最为敏感且具有不可逆性。随着沉积时间的延长,沉积盆地的埋藏深度(H)是会不断增加,从而引起地层温度逐渐升高,进而导致地层中有机质热演化程度的逐步增加。
利用镜质体反射率(R0)估算不整合面地层剥蚀厚度的方法在石油勘探地质领域得到了广泛的应用 [6] [7] [8] [9] 。但有些学者认为将不整合面地层剥蚀的影响处理为不整合面上、下构造层中R0随深度的“跳跃”的唯一原因是不全面的,因为R0值随深度的不连续分布也可能由于古地温梯度变化的影响。换句话说,当诠释镜质体反射率与埋深的耦合性时,剥蚀–反剥蚀的沉降–隆升和古地温梯度变化这两种情况都需考虑。肖贤明等 [10] 以Arrhenius方法为理论基础,应用Karweil图解法,对不同古地温梯度条件下有机质热成熟作用进行了模拟计算,提出了镜质组反射率梯度法确定古地温梯度的方法。Wood [11] 的研究表明对于大部分沉积盆地,地层温度随时间变化率介于0.25℃/Ma~9℃/Ma,平均为1℃/Ma。在地层温度随时间变化率为1℃/Ma时,王玮 [12] 基于简化模型的lnR0-H数据提出地温梯度的求取计算方法。韩永辉 [13] “冷却系时法”理论,把地球看作不断冷却的热体,以现今地温为基准,用经验系数对今地温及古地温梯度进行校正得到古地温。在这些镜质体反射率梯度法与古地温梯度的定量关系中,都简化甚至忽略了时间的作用。本文认为既然温度和时间是两个最为重要的研究镜质组反射率变化参数,那么可以推理时间和镜质体反射率梯度是两个最为重要的研究古地温梯度变化参数。为此将用包含镜质体反射率、古地温、和时间三个变量类似吴冲龙 [14] [15] [16] [17] 煤变质热动力学方程来讨论镜质体反射率梯度法与古地温梯度的定量关系。然后用包含中生界和古近系之间的不整合面探井实测数据 [18] 验证温度、埋深、时间和镜质体反射率的定量关系。
2. 油气钻井与热动力学方程
2.1. 油气钻井
表1为实测该井古近系构造层(15个测点)和古生界些构造层(14个测点)的钻井深度、镜质组反射率及最高古地温数据 [18] 。

Table 1. Original burial depth, vitrinite reflectance, and maximum ground temperature data
表1. 原始埋深、镜质体反射率、和最高地温数据
表1的数据中有实测的埋深、实测的镜质体反射率、最高温度、以及确定的时间(古近系构造层和古生界构造层)。温度将被本文用做于参考温度,和本文中的计算温度进行误差比较。埋深将被用做于参考埋深,和本文中的计算埋深进行误差比较。根据同一构造层中的镜质体反射率R0与时间存在正相关的原理,古近系构造层的15个测点时间是古近系的地质年龄从6500万年起到2350万年止,在古近系构造层,任何镜质组反射率值R0的岩层绝对年龄t为:
(1)
式中:t为岩层绝对年龄,百万年;R0为镜质体反射率,%。
古生界构造层的14个测点时间是从25,000万年起到6600万年止,则在古生界构造层中的任何镜质组反射率值R0所对应的的岩层绝对年龄t为:
(2)
时间长,镜质体反射率大,成熟度高。同时,古近系构造层和古生界构造层的数据是各自独立,并分开计算的。
2.2. 热动力学方程与古地温梯度
吴冲龙参照Bostick曲线和我国中、新生界实测数据,采用双重回归的方法来建立温度–时间–反射率的三变量动力学方程:
(3)
式中:T为古地温度,K。N,M,O和P则为四个待定系数。
2.3. 热动力学方程中系数的求解
虽然煤变质热动力学方程的N,M,O,和P四个参数在原始文献上已经被赋值,但是对于印度尼西亚的探井的古近系构造层和古生界构造层各自的N,M,O,和P四个参数却是未知的。
本文按以下具体操作,采取试差法求解。首先对于一构造层设置一组初始猜测参数代入该构造层所有实测点的镜质组反射率和时间,求解相应各点的温度值,定义为计算温度。计算各点计算温度与表1所列的参考温度的相对误差和该构造层所有点的平均相对误差。再设置一组新的猜测参数值,重复以上计算,求解相应各点新的计算温度值,新的相对误差和平均相对误差,直至平均相对误差达到满意程度。
2.4. 古地温梯度与镜质组反射率梯度的关系
将方程(3)做以下数学处理:
(4-1)
(4-2)
(4-3)
(4-4)
(5)
方程(3)显示古地温是古地质时间与镜质体反射率的函数。方程(4-3)与方程(4-4)的差别仅在于镜质体反射率的差别。根据方程(5),古地温梯度是古地质时间、镜质组反射率、和镜质组反射率梯度的函数。当参数及t都相同的前提下,镜质体反射率的差别造成了所求得的古地温的差别,从而求得古地温梯度。
2.5. 古地温梯度与计算埋深的关系
当T2为(R0+ ΔR0)及t条件下所求得的温度,T1为R0及t条件下所求得的温度,且T0为古地表温度时,古地温梯度与计算埋深H计算的关系可以用下列方程表示:
(6)
列于表1中的实测埋深作为参考埋深用于与相应的计算埋深进行比较,计算各个构造层的相对误差和平均相对误差。平均相对误差则可以作为评价用镜质体反射率梯度求古地温梯度的可行性。
3. 结果与讨论
3.1. 热动力学方程的适用性
表2列出煤变质热动力学参数和最终选定的古近系有机质热动力学参数、和古生界有机质热动力学参数,有学者就煤变质热动力学方程进行过研究 [19] [20] 。

Table 2. Thermodynamic parameters under three different scenarios
表2. 三种情况下的热动力学参数
按表2的热动力学参数代入古近系构造层共有15个测点,计算出该构造层的计算古地温,后计算出以参考古地温为基础的相对误差和平均相对误差。
对于古近系构造层,用最终选定的系数的计算温度与参考温度的平均相对误差为0.71%。从表1中的原始数据看,古近系构造层中有两组点的数据是属于异常点。一个是起始的第二点,还有一个是倒数第二点。
图1是古近系构造层的温度–时间–镜质体反射率关系图。
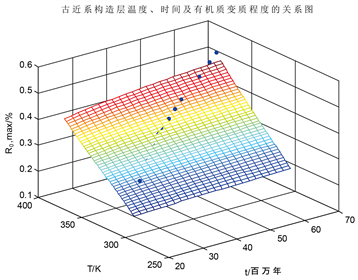
Figure 1. Temperature-time-vitrinite reflectance relationship diagram of the Paleogene tectonic layer
图1. 古近系构造层的温度–时间–镜质体反射率关系图
按表2的热动力学参数代入古生界构造层14个测点,计算出该构造层的古地温,然后计算出以参考古地温为基础的相对误差和平均相对误差。对于古生界构造层,用最终选定的系数计算温度与参考温度的平均相对误差仅为0.31%。
图2是古生界构造层的温度–时间–镜质体反射率关系图。
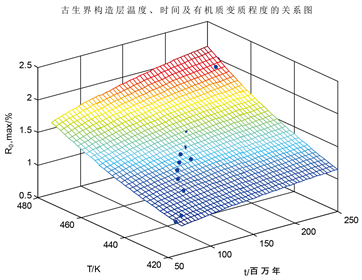
Figure 2. Temperature-time-vitrinite reflectance relationship diagram of the Paleozoic tectonic layer
图2. 古生界构造层的温度–时间–镜质体反射率关系图
3.2. 镜质体反射率梯度对古地温梯度的影响
根据方程(5),古地温梯度是古地质时间、镜质组反射率、和镜质组反射率梯度的函数。假设固定了镜质组反射率梯度,古地温梯度就成为古地质时间与镜质组反射率这两个自变量的函数,因此可以用三维曲面来显示。按表2的热动力学参数,固定了镜质组反射率梯度为0.013%,代入古近系构造层计算在不同古地质时间和镜质组反射率下的古地温梯度,并作图得图3。对于古近系构造层,其古地温梯度为4.28℃~3.02℃每100 m。
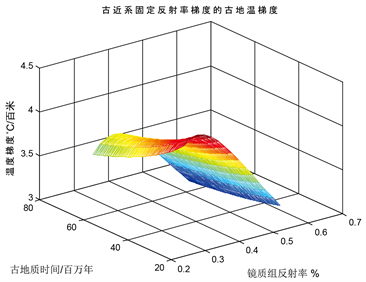
Figure 3. Paleothermal gradient under fixed reflectance gradient in the Paleogene
图3. 古近系固定反射率梯度下的古地温梯度
假设地表温度为15℃,按方程(6)古地温梯度与计算埋深的关系计算古近系构造层的15个测点的计算埋深,最后计算出以参考埋深为基础的相对误差和平均相对误差,列于表3。

Table 3. Comparison between calculated and measured burial depths of the Paleogene
表3. 古近系计算埋深与实测埋深的比较
按表2的热动力学参数,固定了镜质组反射率梯度为0.04%,代入古生界构造层计算在不同古地质时间和镜质组反射率下的古地温梯度,并作图得图4。对于古生界构造层,其古地温梯度为4.87℃~1.85℃每100 m。
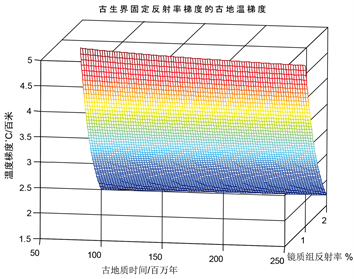
Figure 4. Paleothermal gradient of fixed reflectance gradient in the Paleozoic era
图4. 古生界固定反射率梯度的古地温梯度
按照相同的步骤,假设地表温度为15℃,按方程(5)古地温梯度与计算埋深的关系计算古生界构造层的14个测点的计算埋深,最后计算出以参考埋深为基础的相对误差和平均相对误差,列于表4。

Table 4. Comparison between calculated and measured burial depths in the Paleozoic era
表4. 古生界计算埋深与实测埋深的比较
对于古近系构造层,计算温度与参考温度的平均相对误差为0.71%,而计算埋深与参考埋深的平均相对误差为8.28%。对于古生界构造层,计算温度与参考温度的平均相对误差为0.31%,而计算埋深与参考埋深的平均相对误差为3.94%。对于古地温的平均相对误差小于埋深的平均相对误差最主要的原因分析如下:当计算古地温时,是用镜质体反射率与地质年龄求古地温,只有一次计算误差。当计算古地温梯度时,先是用镜质体反射率、地质年龄以及镜质体反射率梯度求古地温梯度,再用计算来的古地温梯度求埋深,存在两次计算误差。误差叠加使得埋深的平均相对误差大于古地温的平均相对误差。其次,镜质体反射率的变化是不可逆的,但考虑到剥蚀-反剥蚀的互补作用,埋深的变化是可逆的。
4. 结论
① 有机质演化热动力学方程可以用于准确描述古地温与镜质体反射率和岩层绝对年龄的关系,借助镜质体反射率梯度来计算古地温梯度并可以计算出埋深。
② 对于古近系构造层,计算埋深与参考埋深的平均相对误差为8.28%。对于古生界构造层,计算埋深与参考埋深的平均相对误差为3.94%。
③ 计算埋深的平均相对误差均大于计算温度时的平均相对误差。
④ 当诠释不整合面上、下构造层中Ro 随深度的“跳跃”无法耦合时,既要考虑不整合面地层的剥蚀(沉降)–反剥蚀(隆升)的影响,同时需要考虑古地温梯度变化的影响。
基金项目
陕西省教育厅一般专项(23JK0611)。