1. 引言
伴随着科学技术的发展,测绘新技术也在慢慢崛起。其中,三维激光扫描仪的诞生为推动测绘朝着高新技术发展作出了贡献。三维激光扫描仪通过无接触式测量,获取大量具有三维坐标信息的点云数据,通过配准匹配构建三维点云模型,从而实现被测物体三维展示 [1] [2] [3] [4] [5] 。其中,关键技术是点云如何实现高精度匹配配准,形成表面无噪点的点云模型,这是制约点云模型大规模应用的一道障碍。关于配准算法的研究,国内外专家学者做过深入分析探讨,常规模型如全局搜索思想的配准方法、RANSAC点云配准算法、主方向贴合算法、最近点迭代(Iterative Closest Point, ICP)算法等。常规一种算法难以满足点云配准的要求,可将多种算法综合各自优点实现高精度配准,如文献 [2] 中提及利用向量夹角提取特征点后通过快速点特征直方图(Fast Point Feature Histograms, FPFH)描述特征点,并在ICP算法中加入KD-tree完成最终配准;文献 [3] 在ICP算法中利用二次搜索求出最近距离,提高了传统ICP算法的效率;文献 [4] 中涉及在主成分分析法(Principal Component Analysis, PCA)的基础上完成初始配准,但PCA算法要求待配准点云有较高的重叠度;综合已有研究资料表明,配准过程一般包括两个步骤:粗配准与精配准。本文在研究了多种配准算法之后,尝试将主方向贴合算法与改进的ICP算法组合。将主方向贴合算法作为粗配准,得到粗配准之后的点云数据;利用改进的ICP算法作为精配准,最终实现点云三维模型的精确构建。以某三维激光扫描建模工程为例,通过外业获取的点云数据,经过粗配准与精配准两个过程,实现了三维模型的构建,同时验证了该组合方法在点云配准方面的有效性。
2. 配准算法原理
2.1. 主方向贴合算法
该算法的基本思想是解算每个点的特征向量,特征向量中有两个成正交的分矩阵。这两个矩阵能够描述该点的主要位置信息,并能够保存主要信息以简化点云描述部分不对称存在 [6] [7] 。为了提高主方向贴合算法的配准效果,在算法运行前先粗略地针对两站点云进行粗处理,剔除噪声点云并将重叠区域进行提取,其目的是为了提高点云的配准精度与效果。
2.2. 最近点迭代算法
ICP算法经过几十年的发展已日趋成熟,特别是国内外学者针对该算法提出了不同的改进算法。但是该算法使用起来还具有一定的局限性,如点云的重叠率较高、噪点点云数据不能太多。否则,配准的点云效果较差,优势不明显 [8] 。这就需要在使用ICP算法之前,使用粗配准算法将点云数据粗略配准。上文中提及的主方向贴合算法的粗配准能够作为ICP算法的输入数据,从而充分发挥ICP算法的优势,实现点云模型的精确配准。国外专家Besl等人提出了该算法无需控制点即可实现点云的配准,每一次迭代过程中都会重新计算迭代误差,直至迭代差值小于某一阈值。当这一数据值满足要求时,迭代结束,并且此时的特征向量及坐标转换配准参数是唯一解 [9] [10] 。
针对数据点云X,这其中包括该数据集中计算的对应点云,利用ICP算法构成目标点云集合Yk。该过程就是ICP算法的核心思想,以下为描述该计算的主要过程:
(1)
利用四元数算法估算点云集合X、Yk,计算出配准参数如式(2)所示:
(2)
通过变换矩阵H将点云集合X中每个数据点旋转平移变换,如式(3)所示:
(3)
式(1)至式(3)为经典ICP算法的主要流程,该算法搜寻最近点并不断逼近最佳值,通过四元数算法获取参考点云与目标点云之间的配准参数。
假设目标数据和参考数据分别为X、Y,其迭代的步骤如下:
1) 寻找最近点:由公式
对点云数X中的每个数据点,计算其在点云数据Y中的最近点,构成点集Yk;
2) 估计配准参数:最小化目标函数,计算配准参数H,
,并且计算估计误差d;
3) 更新数据集:由公式
,利用变换矩阵H对数据集X进行更新 [10] ;
4) 迭代计算:对更新后的数据集重复1)、2)操作,得到新的配准参数H'和估计误差d'。如果连续两次计算得到的估计误差变化小于某一阈值
时,即为
,则停止迭代,输出结果。
ICP算法还需要满足的要求是对于两个数据集,其中一个数据是另一个数据的严格子集,那么才能够使得两个待配准的点云数据总体上在某一种度量准则下达到最佳配准。在进行三维数据扫描时,无法一次性的获取物体表面的全部点云数据,往往要从不同的角度下采集物体的局部数据,这些数据仅仅是部分相互重叠的,所以,ICP算法得到的结果可能不会是全局最优化,这就需要对迭代初始相对位置的要求较高,不能够与真实的位置相差过大。
2.3. 改进的ICP算法
经典ICP算法如上文介绍实现流程,以欧式距离为限制条件搜寻源点云P中的某个点
在目标点云Q中的对应点
,并将对应点计算的旋转矩阵R与平移矩阵T,使得按照如下公式计算的误差最小。
(4)
按照式(4)的计算方式将目标点云与源点云所有数据参与计算,但存在噪点导致计算效率降低。因此,在传统ICP算法基础之上,加入法向量夹角阈值删除未参加配准的噪点,来优化算法的执行效率。流程如下所示:
1) 经过主方向贴合算法粗配准之后的源点云为
,目标点云集合为
,分别计算出每个点的法向量;
2) 针对
中的每个点在
中查找对应的欧氏距离最近点,记为点对N,随后设置法向量阈值为
,假如N的法向量夹角小于阈值,保留该点对,否则视为匹配失败点对,将其剔除,剔除的点对记为
;
3) 根据点对集合
利用奇异值分级法计算变换矩阵(R、T),并根据误差函数
求出最优的变换旋转矩阵。
3. 实验验证
文中评定最终配准结果精度采用均方根误差(RMSE),其计算公式为:
(5)
其中,
与
分别表示目标源点与目标点中对应点,n表示对应点数量。
3.1. 实验一
3.1.1. 粗配准
本文采用了主方向贴合法对点云数据进行粗配准,算法验证所采用的数据格式为asc,数据来自某数据库中的标准参考格式数据,目标点云数量为39,910个,参考点云数据量为39,930个。
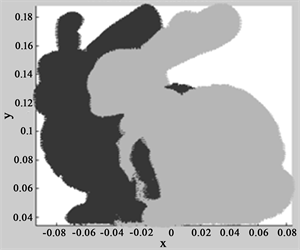
由图1配准前的点云数据可知,目标点云与参考点云两者之间重叠率较高,无需进行预处理可对点云数据求解特征向量与特征值的计算。利用Matlab软件编程实现主方向贴合算法,在编程实现过程中发现该算法思想简单易于实现。最终通过程序实现了主方向贴合算法,如图2所示。虽然数据量较大,但过程仅花费0.084878秒,再次印证了该算法易于实现且较简单的优点。
主方向贴合法不同于RANSAC配准算法中要求点云数据中点的数量必须相同,它是对点云数据分别计算的,所以可以对不同大小的点云数据进行计算。
虽然主方向贴合法有上述种种优点,但是该算法的缺点也非常明显。如该算法在配准之前,要求原始点云数据具有较大的重叠率,如重叠率较小则无法实现配准。且该算法受噪点影响也较大,时常配准效果不明显,精度较差。必须在配准之前去噪,本小节采用的标准库中的点云数据,是经过去噪之后处理,所以在算法运行中有一定优势。同时,在外业中增加点云重叠率等一系列操作,这样才能打破该算法的局限性,提供应用场景。
 (a) (b)
(a) (b)
Figure 1. 2D and 3D display before registration: (a) 2D display; (b) 3D display
图1. 配准前二三维显示:(a) 二维显示;(b) 三维显示

 (a) (b)
(a) (b)
Figure 2. 2D and 3D display after rough registration: (a) 2D display; (b) 3D display
图2. 粗配准之后二三维显示:(a) 二维显示;(b) 三维显示
采取了人机结合的方式,即对于重叠区域小的两个点云数据,粗略地选取其可以重叠的部分,然后再对这一部分进行配准,得出的旋转矩阵R、平移矩阵T再作用于原数据,可以达到预期的效果。这种方式需要判断出点云数据中重叠的区域,这就需要在采集数据同时收集相关的资料,方便在处理数据时判断点云数据重叠区域的大体位置。本文在实例部分所用的点云数据就是重叠率小的数据,需要在配准前粗略地选取点云可以重叠的部分。
3.1.2. 精配准
改进的ICP算法在主方向贴合算法运行之后的结果运行,设置阈值
,经过9次迭代之后配准效果如图3所示,精度统计如表1所示。改进的ICP迭代算法配准效率高且配准精度较传统ICP方法高。
 (a) (b)
(a) (b)
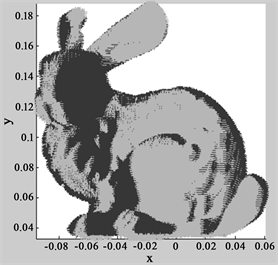
Figure 3. 2D and 3D display effects after fine registration: (a) 2D display; (b) 3D display
图3. 精配准之后二维、三维显示效果:(a) 二维显示;(b) 三维显示

Table 1. Comparison of registration time and error
表1. 配准耗时、误差对比
调试之后,将图像用Matlab显示,由图3可知,代码编写可行。整个运算过程中,每个数据的点的个数为40,000多个,迭代运行9次,一共耗时为0.190162秒。无论是二维、三维,配准效果均满足要求。同时,由表1可知,改进的ICP迭代配准算法较传统ICP迭代算法在配准耗时与精度方面均有提高。其中,在相同点云数量配准中,改进的ICP较传统ICP配准耗时缩减4倍有余;精度方面提高2倍有余;证明了本文的组合算法思想可信性。
改进的ICP迭代算法的精髓在于阈值设置的大小。该值设置的大小又决定了运算时间,两者之间看似矛盾,但可通过调整阈值并考虑计算时间来衡量。特别是过小的阈值,直接造成增加几何量级的迭代计算,带来的后果就是计算时间的增加。所以如何选取合适的阈值,成为改进的ICP迭代算法成功实现的关键因素,而确定阈值可通过实验经验确定,也可通过误差反向传播定律等方法实现。改进的ICP算法思想明确,简单且易编程实现,但是其特性也决定了该算法运行所需的条件较高,为了实现它就必须达到所规定的条件。因此,必须在使用改进的ICP算法之前,先对点云数据进行粗配准,给出一个比较理想的初始对应位置。
3.2. 实验二
根据上文中提及的外业采集数据流程,采集对象为某一大学校门。该校门高度12.3米,宽度8.45米,厚度2.70米,为钢筋与混凝土结构。通过实地调查踏勘,采用四站全包围方式进行点云采集。可提前通过(Real-Time Kinematic, RTK)测量方式实测图根点作为标靶,作为将点云模型转换至当地空间坐标系的参考点。将该校门点云数据去噪之后的背面模型展示如图4所示,正面效果图如图5所示。为运行IICP算法,利用专业的点云数据处理软件拼接,效果如图6所示。为配准点云数据首先确定重叠区域为门内测;其次运用主方向贴合算法进行粗配准;最后利用IICP算法将粗配准之后的点云数据精确配准得到效果如图7所示。最终对配准的结果精度验证与评定工作,经过统计该次配准的误差为0.0593。即在本文要求精度需要达到对应点之间的距离不大于30 mm的条件下,点云数据中未达到配准要求的点所占的比率为0.0593。表2为改进ICP算法与传统ICP算法在耗时、精度两方面的统计。与实验一结论相似。改进的ICP迭代配准算法在精度与耗时中均由于传统ICP算法,再次证明了改进的ICP算在配准中的优势性。

Figure 4. 3D display of the back of the school main gate
图4. 该学校正门背面三维显示

Figure 5. 3D display of the front of the school main gate
图5. 该学校正门正面三维显示
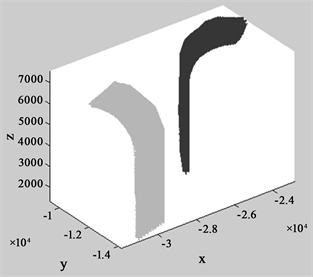
Figure 6. Point cloud rendering before misregistration
图6. 未配准前点云效果图
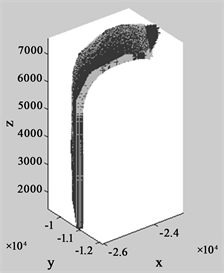
Figure 7. Point cloud rendering of rough registration and fine registration
图7. 粗配准与精配准点云效果图

Table 2. Comparison of registration time and error
表2. 配准耗时、误差对比
4. 结论
本文在经典ICP算法的基础之上,研究了改进的ICP算法与主方向贴合算法的结合实现点云配准。并深入分析了两者的适用条件,利用Matlab编程软件实现了这两种算法。通过外业实测点云数据,并利用实验一与实验二过程,陈述了粗配准中利用主方向贴合算法、精配准中利用改进的ICP迭代算法。并比较分析了通过改进ICP算法实现了点云配准效率的提升,配准误差也得到较大提升。文中两组实验均是基于点云重叠度较高为基础的,低重叠度的点云数据配准是下一步研究工作的重点。