1. 引言
近场声全息技术 [1] 能从声场中部分点的声压或者质点振速,还原出声场中全部的声学参数。近场声全息技术要求应用的环境为声自由场,然而在工程实践中,环境对目标噪声源的辐射声波的反射作用使得目标声源的辐射声和反射声叠加在一起形成了非自由声场。如果在非自由声场中直接采用传统的近场声全息的技术重构声源,将产生较大的重建误差,有时甚至产生错误的结果。
为了在非自由场中应用近场声全息技术,学者们采取了两大类的方法来消除反射声的影响。一类是根据反射材料的性质修改声场传递矩阵从而重建目标噪声源,周达仁 [2] 和Elias [3] 采用第一类方法通过修改声场传递矩阵直接重建目标噪声源,他们分别在已知反射材料的声阻抗和未知反射材料的声阻抗两种条件下对目标噪声源进行了重构,从他们计算的结果来看,当反射材料的声阻抗未知时,直接重构的声源误差较大。一类是在使用传统的近场声全息技术重建目标噪声源前进行声场分离。声场分离的方法有一个优点就是不需要知道反射材料的声阻抗,在声场分离方法中主要有快速傅里叶变换法 [4] 、球面波叠加法 [5] 、等效源法 [6] - [11] 、和最优统计近场声全息方法 [12] - [18] 。大量的学者对声场分离进行了研究,文献 [19] 通过分布式球形阵列获取声学参数,利用球谐函数对声场进行分解,获得目标声场与干扰声场的球谐波展开系数,进而估计目标声场,文献 [20] 通过稀疏正则化的方法,通过等效源法将干扰声源的声场分离,进而虚拟出自由声场。文献 [21] 基于Helmholtz方程最小二乘法降低声场分离误差,并重建了声场,从数值仿真来看,达到了比较好效果。这些方法都能达到一个较好的声场分离的效果,但是这些方法的显著的缺点是需要采集两个不同位置全息面的声压,大大增加了声场测量的工作量。
为了大大减小声场测量的工作量,本文提出的基于虚拟双全息面的声场分离方法只需要获取一个全息面的声压就能较为准确的将声场中的反射声剔除,从而形成虚拟的声自由场。
2. 理论研究
大型机器设备等一般放置在厂房中或地面上,机器运行时产生振动并向四周辐射声波,当声波遇到地面等时会产生反射,声场中任一点的声压为机器声源的辐射声和地面反射声的叠加,此时如果直接采用传统近场声全息方法重建声源将造成较大误差。为了准确测量大型机器的噪声辐射声波并重构噪声源,文章提出了基于虚拟双全息面的声场分离方法。声场分离过程中主要采用的理论是虚源理论 [2] 和球面波叠加理论。
机器、机器通过地面的反射形成的虚源和全息面的示意图如图1所示。图1中的实线箭头表示辐射声波,虚线箭头表示反射声波。从图中可以看出,全息面测得的声压为机器辐射声压和地面反射声压的叠加和。由于地面会吸收一部分入射的声波,所以地面不可能是完全刚性的反射面,因此虚源的强度要小于实际机器声源的强度。分别以机器形心和虚源形心为坐标原点建立球坐标系
和
,将全息面向远离机器方向移动距离微小的距离形成虚拟全息面,由于距离d很小,所以可以认为全息面和虚拟全息面都处于目标声源的近场。
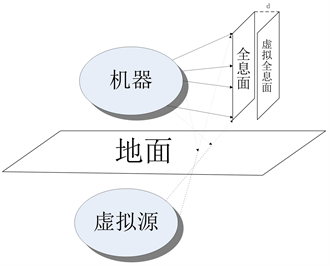
Figure 1. The diagram of machine, virtual source and holographic surface
图1. 机器、虚源和全息面的示意图
如图1所示,假设全息面共有N个测点,由于声压的标量特性全息面的测量声压有如下的关系:
(1)
上式中
表示全息面上的测量声压,为N行声压列向量,
表示目标声源在全息面上产生的N行声压列向量,
表示虚源在全息面上产生的N行声压列向量。
目标声源在全息面上第 个测点的声压分量可以用式(2)表示:
个测点的声压分量可以用式(2)表示:
(2)
式中
表示全息面第i个测点在以
为原点的球坐标系中的坐标,
表示第一类汉克尔函数,
表示球谐函数。
全息面有N个测点,那么式(2)中
,有N个类似于式(2)的等式,写成矩阵形式如式(3)所示:
(3)
同理,虚源在全息面上第i个测点的声压分量可以用式(4)表示:
(4)
式中
表示全息面第i个测点在以
为原点的球坐标系中的坐标,
表示第一类汉克尔函数,
表示球谐函数。
式(4)中
,那么有N个类似于式(4)的等式,写成矩阵形式如式(5)所示:
(5)
由于虚拟全息面是全息面向远离声源方向移动一定距离d形成的,所以其上的所有参数和全息面是一样的,同样也有N个测点,声压在虚拟全息面上声压的关系也为代数叠加关系,如式(6)所示。
(6)
上式中
表示虚拟全息面上的N行声压列向量,
表示目标声源在虚拟全息面上产生的N行声压列向量,
表示虚源在虚拟全息面上产生的N行声压列向量。
目标声源在虚拟全息面上第j个测点的声压分量可以用式(7)表示:
(7)
式中
表示虚拟全息面第j个测点在以
为原点的球坐标系中的坐标,
表示第一类汉克尔函数,
表示球谐函数。
式(7)中
,那么有N个类似于式(7)的等式,写成矩阵形式如式(8)所示:
(8)
同理,虚源在虚拟全息面上第j个测点的声压分量可以用式(9)表示:
(9)
式中
表示虚拟全息面第j个测点在以虚源为原点的球坐标系中的坐标,
表示第一类汉克尔函数,
表示球谐函数。
式(9)中
,那么有N个类似于式(9)的等式,写成矩阵形式如式(10)所示:
(10)
由式(3)得
(11)
将式(11)代入式(8)得
(12)
由式(5)得
(13)
将式(13)代入式(10)可得
(14)
由式(1)得
(15)
将式(15)代入式(14)得到
(16)
联立式(6)、式(12)、式(16)得
(17)
其中
,
。
根据平面波理论可以得出,目标声源的声波以平面波的形式从实际全息面传播到虚拟全息面,有
(18)
对式(18)两边同时进行二维傅里叶变换有
(19)
其中
。
当
时,
,即传播波从实际全息面传播到虚拟全息面时声压角谱幅值大小不变只是相位发生变化。
当
时,
,即倏逝波从实际全息面传播到虚拟全息面时,声压角谱幅值呈负指数关系递减而相位不发生变化。
虚源的声波以平面波的形式从实际全息面传播到虚拟全息面,有
(20)
其中
。
当
时,
,即传播波从实际全息面传播到虚拟全息面时声压角谱幅值大小不变只是相位发生变化。
当
时,
,即倏逝波从实际全息面传播到虚拟全息面时,声压角谱幅值呈负指数关系递减而相位不发生变化。
从式(19)和式(20)知,当
时,
和
均为
,目标声源和虚源的传播波从实际全息面传播到虚拟全息面时声压角谱幅值大小不变只是相位发生变化。当
时,
和
均为
,目标声源和虚源的倏逝波从实际全息面传播到虚拟全息面时,声压角谱幅值呈负指数关系递减而相位不发生变化。当虚拟全息面和实际全息面的距离
时,
和
均趋向1,可以认为传播波的相位没有发生变化,倏逝波的幅值没有发生变化。有
(21)
对式(21)进行二维傅里叶逆变换有
(22)
式(22)代入式(17)得
(23)
其中
,
。
式(23)即为基于虚拟双全息面的声场分离方法的公式,
即为目标声源直接辐射声压。
公式推导的过程中一个条件必须满足:距离d必须较小,以保证实际全息面和虚拟全息面都在目标声源的近场范围内,另外一个原因是声波从实际全息面传播到虚拟全息面时为了保证传播波相位改变很小和倏逝波幅值改变很小。声场分离后即可按照常规的近场声全息方法计算重构面声压和预测面声压。
3. 数值仿真
脉动球、反射材料和全息面的空间布置如图2所示。脉动球的半径r = 0.1 m,脉动球以f = 500 HZ的频率振动,振动的速度v = 0.08 m/s,全息面与反射材料表面垂直,中心距离脉动球中心的距离R = 0.2 m,全息面为1 × 1 m2的矩形,其上均布12 × 12个测点。根据虚源理论,当脉动球振动向四周辐射声波时,在脉动球关于反射材料的镜像声源处会产生一个脉动球的虚源。全息面向远离脉动球的方向移动d1 = 0.0068 m产生虚拟全息面,声压重构面距离全息面d2 = 0.1 m,声压预测面距离全息面d3 = 0.3 m。在数值仿真计算中,全息面测点获取的声压采用文献 [22] 中的方法计算得出。为了定量考察文章提出的声场分离方法重构和预测声压面的效果,定义误差如下:
(24)
表示分离误差,即声场分离后全息面的声压和目标声源的理论声压之间的关系。
(25)
表示原始误差,即声场分离前全息面的声压和目标声源的理论声压之间的关系。
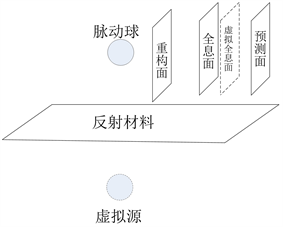
Figure 2. The diagram of pulsating sphere, reflective material and holographic surface
图2. 脉动球、反射材料和全息面布置图
为了使仿真更加接近实际,在仿真中加入
的高斯白噪声,仿真选取的最优球面波展开阶数为4阶,采用的正则化方法为标准的tikhonov方法,正则化参数的选取采用L曲线选取。仿真图如图3所示。
从图3中可以看出,声场分离前全息面测点的声压幅值和理论值相差较大,通过式(25)计算出误差为793.88%,采用虚拟双全息面分离声场后测点的声压幅值和理论值非常接近,通过式(24)计算出误差为1.72%。仿真结果表明本文提出的虚拟双全息面分离声场的方法能非常有效地抑制反射声的干扰。
4. 参数讨论
在虚拟双全息面分离声场的方法中,声场的频率、测点的间隔、虚拟全息面和实际全息面的距离是重要的参数,这些参数对声场分离的精度产生重要的影响。
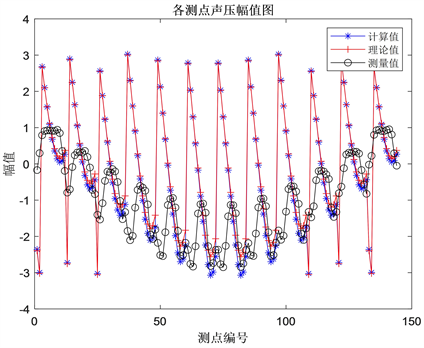
Figure 3. The diagram of the sound pressure amplitude of every measuring point
图3. 各测点声压幅值图
4.1. 分析频率
改变分析频率,其余仿真参数保持不变,每隔50 Hz计算声场分离的误差,画出声场分离的误差随频率变化的曲线如图4所示。

Figure 4. The diagram of sound field separation errors variation with frequency
图4. 声场分离误差随频率变化曲线
从图4中可以看出,在各频率下声场分离的误差非常小并且随着分析频率升高,声场分离的误差呈下降趋势,当分析频率为350 Hz以上时,声场的分离误差在0.1%以下,表明声场分离后,计算声压值和理论声压值非常接近。
4.2. 测点间隔
改变测点间距,其余仿真参数保持不变,画出声场分离的误差随测点间距变化的曲线如图5所示。

Figure 5. The diagram of sound field separation errors variation with distance between measuring points at different frequencies
图5. 不同分析频率时声场分离误差随测点间距变化曲线
从图5中的曲线可以看出,在不同的分析频率时声场分离的误差随测点间距的减小而减小,这是由于当一个波长跨过的测点数越多时,测点接受的声波参数越能精确描述声波波形,使得分离误差降低。当测点间距为1/12 m (0.083 m)时,声场分离的误差趋于稳定。对于频率为1000 Hz的声波来说,其波长为0.34 m,测点间距约为波长的1/4,即一个波长完整的跨过5个测点,此时声场分离误差最小。虽然根据抽样定理,测点间距为波长的1/2时即可完整的复现信号,但是对于声场分离的误差会增大,增大的误差在重建目标声源时会被放大,从而造成错误的重建结果。
4.3. 虚拟全息面和实际全息面距离
虚拟全息面和实际全息面的距离对声场分离的误差产生非常重要的影响,把式(17)重新抄写如下:
(17)
其中
,
。
从上式中可以看出辐射声的声压和
、
、
、
的运算结果有相当大的关系,即辐射声的声压主要由虚拟全息面到实际全息面的距离影响。当距离过小时
的奇异性非常大,广义逆的求取过程中虽然采用了正则化方法稳定逆运算的结果,但是分离出的辐射声声压误差仍然较大,当距离过大时,虚拟全息面的声压
大大小于实际全息面的声压
,如果继续按照式(24)计算声场分离后的辐射声声压,必然会造成较大的误差。声场分离的误差在声源重建时会被放大,过大的声场分离误差往往会导致错误的重建结果。
改变虚拟全息面和实际全息面的距离(取波长倍数),其余仿真参数保持不变,画出声场分离的误差随虚拟全息面距离变化的曲线如图6所示。
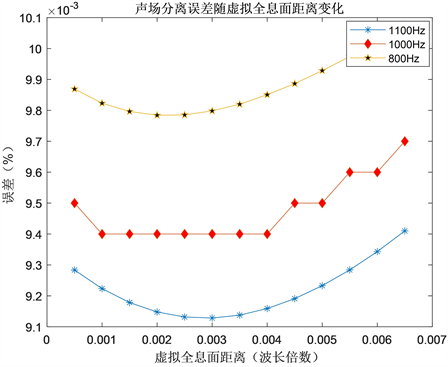
Figure 6. The diagram of sound field separation errors variation with distance between the holographic surface and the virtual holographic surface at different frequencies
图6. 不同分析频率时声场分离误差随虚拟全息面距离变化曲线
从图6中可以看出,在不同的分析频率下,声场分离误差随虚拟全息面距离变化的趋势基本相同,当虚拟全息面距离非常小时,声场分离的误差较大,达到了0.1%,当虚拟全息面的距离增大时,声场分离的误差慢慢减小,综合3条曲线当虚拟全息面的距离为0.0025倍波长时,声场分离误差最小,之后随着虚拟全息面距离增大,声场分离的误差增大。
5. 结论
为了从目标噪声源的辐射声、反射声的混合声场中分离出辐射声,同时兼顾声场测量工作的便捷性,本文提出了基于虚拟双全息面的声场分离方法,该方法不需要知道反射材料的声阻抗特性。方法的理论推导基于虚源理论和声波的球面波叠加方法得出声场分离的基本公式,用置于反射材料前的脉动球进行了仿真,验证了本文所提方法的有效性,并对声场的频率、全息面测点间距和虚拟全息面的距离等3个对声场分离误差由重大影响的参数进行了仿真研究,得出如下结论:
1) 随着分析频率升高,声场分离误差下降;
2) 随着全息面测点间距减小,声场分离的误差下降,当测点间距为声波波长的1/4时声场分离误差最小;
3) 声场分离误差随虚拟全息面的距离的增大呈现先减小后增大的趋势,当虚拟全息面的距离为波长的0.0025倍时,声场分离误差最小。
基金项目
国家重点研发计划(2017YFC0307501);国家自然科学基金青年基金(51705145);国家自然科学基金青年基金(41906162)。
NOTES
*通讯作者。

