1. 引言
变压器作为一种重要的电气设备,主要利用电磁感应的原理来实现电路中的能量传送和电压、电流、阻抗及相位变换等功能,具有工作性能好,运行安全可靠和转换效率高等优点,被广泛应用于电力工程系统、高压驱动、无线电技术和自动控制系统等领域。随着自然资源的日益枯竭,降低变压器的各种损耗,提高变压器的运行安全性和工作效率,优化变压器整体设计已成为当前研究的一个重要课题。目前,许多研究学者围绕着变压器开展了一些列的研究工作 [1] - [6] 。于继来等人分析了各种移相调节变压器的共同性质,讨论了移相调节变压器损耗处理方法和容量的计算问题 [7] 。2000年薛向党等在地磁感应电流的基础上,利用时域一频域法对电力变压器特性进行了研究,建立了相应的等效非线性模型,详细分析了仿真结果和实验的误差来源 [8] 。Zhang Yu等研制了一种基于闭合磁芯的小型高压脉冲变压器,该脉冲变压器对脉宽为5~100 s、频带为100 Hz~500 kHz的方形电压脉冲具有良好的响应能力,可以应用于介质阻挡放电和高压纳秒脉冲发生器 [9] 。为了应对高压电网建设带来的新挑战,李东等对移相变压器的研究进行了充分调研,总结了当前移相变压器的核心技术和相关应用,讨论了它们在电气电力系统的稳定性中所起的关键作用 [10] 。Shi yan等通过提高输入气压、输出油压和面积比,提高了高压变压器的输出功率,为气动液压高压变压器的性能与设计优化研究提供了参考 [11] 。为提高变压器的运行特性,陈旭从双绕组变压器的等效电路出发,基于变压器核心技术参数,理论上分析了变压器的有载无载调压、短路电流和空载合闸等特性 [12] 。王帅兵团队基于串联耦合变压器在UPFC系统中的作用,利用双回路和磁路的对偶原理,完成了磁路模型到电路模型的成功转换。同时利用涡流效应和磁路法实现了对漏感参数的计算和仿真电路模型的构建,对变压器的低压物理样机进行了实验和仿真计算,分析了相应的结果吻合情况 [13] 。为提高多电平换流器(MMC)型直流变压器的转换效率,丁然等人基于故障电流的建模,计算出了短路电流峰值和时间之间的对应关系,实现了对限制电流进行调节的目的 [14] 。He Zhimin课题组建立了耦合变压器的功率输出模型。分析了变压器输出功率与相关参数的对应关系,得到了耦合变压器的输出功率特性曲线,讨论了磁芯气隙厚度与最大输出功率的关系 [15] 。吴争研究团队基于多通道接口的电力电子变压器实现了交直流混合电力系统的搭建,在更大范围内增强了系统控制的力度,并探讨了该交直流混合电力系统的关键技术 [16] 。Kladukhin等阐述了特斯拉变压器理论的基本要素,给出了变压器电路中电流和电压动态方程的精确解,在电流和电压恒定的假设下,通过电路的广义参数,给出了变压器二次电路电容存储充电过程中第一和第二半波的最优传输特性,证明了特斯拉变压器的性能 [17] 。Górecki对三种桥式变换器进行了实验研究,根据所得到的变压器铁心参数与输出电压之间关系的测量结果,讨论了全桥变换器的能效问题,提出了SPICE程序中变压器建模的方法,以含粉状铁芯变压器为例,验证了该模型的正确性 [18] 。鉴于目前变压器在日常生活中的重要应用,本文基于交流电源、变压器装置、滑线变阻器、万用表和单芯连接线等实验设备,通过对变压器的基本结构、工作原理和输出特性的详细分析,从实验上研究了变压器的变换和运行特性。
2. 实验原理

Figure 1. Transformer equivalent circuit
图1. 变压器等效电路
变压器运行时的等效电路如图1所示。其中
、
、
、
、
、
、
分别为初级绕组的匝数、电阻、电感、漏电感、路端电压、绕组电流、感应电动势,
、
、
、
、
、
、
、
分别是次级绕组的匝数、电阻、电感、漏电感、路端电压、绕组电流、感应电动势、负载,M是初、次级绕组间的互感系数。变压器空载运行时,加在初级绕组上的交流电压
将在绕组中产生一个交变的空载电流
,铁芯将
产生的交变磁场的绝大部分耦合到次级,在次级绕组中产生感应电动势
。变压器次级接上负载
后,次级电路在
的作用下产生电流
。
所产生的交变磁场的绝大部分磁通又通过铁芯耦合到初级,使初级电流发生改变,由
变为
。变压器的初、次级通过多次相互作用后达到平衡,初级电流
中由次级电流
引起的那部分电流
称为反射电流。
设变压器输入电压的角频率为
,则可根据基尔霍夫定律写出初、次级绕组电压平衡方程为:
(1)
(2)
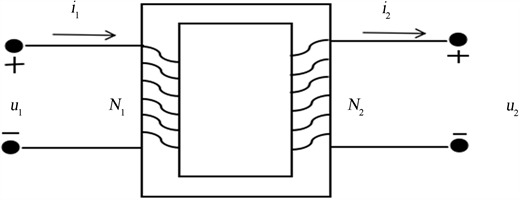
Figure 2. Structural schematic diagram of the ideal transformer
图2. 理想变压器的结构示意图
无漏磁、无绕组电阻、无铁损耗的变压器称为理想变压器,其结构示意图如图2所示。无漏磁表示耦合系数
,为全耦合,其中M为互感,
为一次侧电感值,
为副边电感值,M、
、
均为无限大;无绕组电阻表示初次线圈零电阻,不会产生焦耳损耗;无铁损耗是指铁芯所产生的磁滞损耗和涡流损耗可进行忽略。
由理想变压器的条件可将初、次级电路的电压平衡方程改写成:
(3)
(4)
利用式(3)和(4),可得
(5)
其中K为线圈的匝数比,负号表示
和
的相位差为
。将变压器空载运行时的
代入(3)式可得
(6)
设变压器在负载运行情况下输入电压
保持不变,那么将(6)式代入(3)式可得反射电流与负载电流的变比公式
(7)
式中负号同样表示
和
的相位差为
。次级负载对初级电流的影响可以看作是在初级电路中增加了一个等效阻抗
,则
(8)
因此通常利用理想变压器的阻抗变换来进行阻抗匹配来确保次级电路中负载获得最大输出功率。
3. 变压器的变换和运行特性实验研究
3.1. 开路下次级电压的测量
3.1.1. 次级电压与初级电压的关系
固定初级绕组匝数与次级绕组匝数比为
;将初级电压
从2.4 V始,测量了不同匝数比之下输出电压
。
由图3可知,次级电压与初级电压的关系成线性
分布,其中a为次级绕组匝数与初级绕组的匝数之比:
,b为两个线圈电磁感应造成的损耗,主要包括线圈内阻引起的铜损耗和由铁心引起的铁损耗两部分,本实验采用的变压器的损耗比较低,可以忽略不计。在相同的初级电压下,随着a值的增加,次级电压也相应地增加。
3.1.2. 次级电压与初级绕组匝数的关系
调节变压器次级线圈匝数
匝,初级电压
,改变初级匝数
的值分别设为14;28;42;56;70;84;98;112;126;140,记录所对应的次级开路电压
。
由图4可知,次级开路电压与初级匝数成反比关系:
,其中
,即随着初级匝数的不断增大,次级开路电压不断减小。
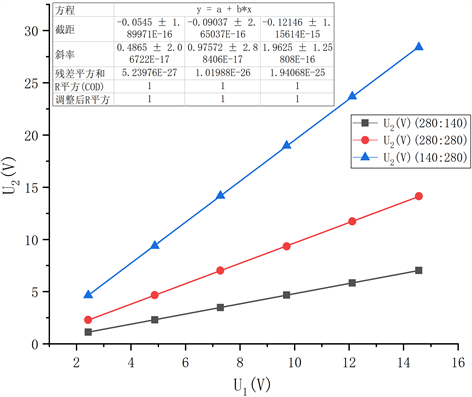
Figure 3. Relationship between secondary open circuit voltage and primary voltage
图3. 次级开路电压与初级电压的关系

Figure 4. Relationship between secondary open circuit voltage and primary turns
图4. 次级开路电压与初级匝数的关系
3.2. 短路时次级电流的测量
3.2.1. 次级短路电流与初级电流的关系
固定初级线圈与次级线圈的匝数比为
,测量不同匝数比下
的输出电流。

Figure 5. Relationship between secondary short-circuit current and primary current
图5. 次级短路电流与初级电流的关系
由图5可知,在短路下次级短路电流与初级电流的关系:
,其中
为初级匝数与次级匝数比值,
为两个线圈电磁感应造成的损耗。随着初级电流的不断增大,次级短路电流也相应随之增加。相同的初级电流下,随着初级线圈与次级线圈匝数比的减小,次级短路电流逐渐减小;同一初级线圈与次级线圈匝数比下,随着初级电流的增加,次级短路电流也相应随之增加。
3.2.2. 次级短路电流与次级线圈匝数的关系
调节变压器初级线圈匝数
匝,初级电流
,改变次级匝数
的值分别为28;56;84;112;140;168;196;224;252;280,记录所对应的次级开路电流
的值。

Figure 6. Relationship between secondary short-circuit current and secondary turns
图6. 次级短路电流与次级匝数的关系
由图6可知,次级短路电流与次级匝数成反比例关系
,随着次级匝数的增加,次级短路电流呈现不断减小的趋势。实验值与理论值存在偏差主要原因在于前期次级匝数较少时损耗主要来源于耦合时产生的磁损耗,随着次级匝数的增多,损耗主要来源于线圈中电流的焦耳热。
3.3. 带载下次级电流与初级电流的关系
固定初级线圈与次级线圈的匝数比为
,
,改变初级电流
的值分别为80;190;280;380;470 mA,记录对应的次级电流
。
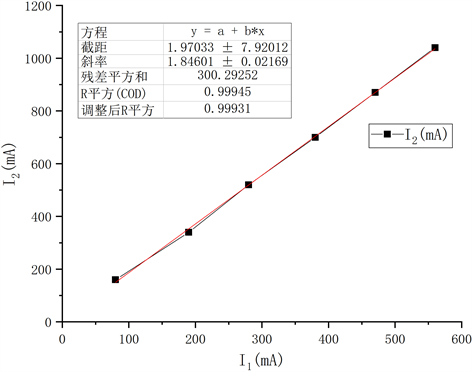
Figure 7. Relationship between secondary current and primary current under load
图7. 带载下次级电流与初级电流的关系

Figure 8. Output power of transformer under load
图8. 带载下变压器的输出功率
由图7可知在次级线路带有负载情况下,初级电流与次级电流满足关系:
,其中
,
为电路中的损耗,主要为电路中负载产生的焦耳热。随着初级电流的逐渐增加,次级短路电流的数值呈线性增加。同时,
的数值和负载的大小之间满足欧姆定律,负载越大,
的值越小,反之越大。
3.4. 带载下变压器的输出功率测量
固定初级线圈与次级线圈的匝数比为
,
设置为4 V,在R开路时调节,调节次级电流
从0开始,记录所对应的
、
、
的值,根据公式
计算纯电阻的输出功率。
由图8可知,在固定负载、初级线圈与次级线圈的匝数比一定时,随着电路中次级电流的增加,输出电压呈现逐渐减小的趋势,输出功率呈现先增大再减小的变化趋势。产生这种现象的原因在于:本实验选用的负载为纯电阻,负载功率因数角与变压器内阻抗角基本相同,故变压器的输出电压U2随着输出电流I2的增加而减小;变压器的空载损耗主要是铁损,负载损耗主要为铜损,负载损耗是随输出电流的变化而变化。当输出电流比较小时,电路中的铜损比起输出功率增大比例要小,随着输出电流的不断增加,电路中的铜损迅速上升,增大比例将大于输出功率增大比例,此时电路的效率开始下降,因此使得输出功率呈现减小的趋势。
4. 结论
随着现代电子电力技术与社会发展的紧密相连,变压器作为一种特殊的电气设备其发挥的作用越来越重要,因此对变压器的输出特性进行研究是十分必要的。本文从实验上研究了在开路下次级电压与初级电压、初级线圈匝数;短路时次级电流与初级电流、次级线圈的匝数;带载下初级电流与次级电流和变压器的输出功率特性。研究结果表明:在固定负载、初级线圈与次级线圈的匝数比一定时,随着电路中次级电流的增加,输出电压呈现逐渐减小的趋势,输出功率呈现出逐渐增大,达到一定值后再逐渐减小的变化趋势。该研究工作为提高变压器的输出特性和优化设计,实现变压器的高效、低损和可靠运行奠定了基础。