1. 引言
中国经济已经进入不同以往的、相对稳定的状态。我国经济工作现在面临的问题是产业结构转型和经济高质量发展。“教育兴则国家兴,教育强则国家强”,也即意味着教育可能与经济发展水平有一定联系,基于此,本文去探究了教育与经济发展水平的关联性。另外,我国当前各个地区之间的经济发展水平存在一定差距,人力资本也存在一定差距,进而本文从时空角度去更全面地查看教育与经济发展水平的关联。
关于教育与经济增长的关系研究最早追溯到经济学家Solow [1] ,他把教育看作经济增长的重要因子,将“残差”效益归功于技术进步,间接肯定了教育对经济发展的积极作用。人力资本理论创始人Schultz [2] 、Griliches [3] 、Jorgenson and Fraumeni [4] 肯定了教育对经济增长的促进作用,分别运用经济增长余数分析法、因素分解法等计量方法推算出美国教育或人力资本对经济增长的贡献率为33%、20%和26%。Khalifa [5] 以6个国家的时间序列数据,分析了在不同国家,教育与经济的发展的联系。Papadakis [6] 通过面板数据的估计阐明中东和北非地区国家的经济复杂性和教育可持续性。Narmadityafe [7] 分析出了经济在家庭教育之间充当中介作用。Saud [8] 分析了欧洲教育政策在经济理论基础下发展的内部联系。
国内还有大量的相关研究,比如朱健和刘艺晴 [9] 、李国柱和张梦奇 [10] 、张波和张放平 [11] 等。在研究内容上,以往研究主要集中于教育对经济增长的影响或者贡献、以及两者的相互作用关系,少量学者针对教育投资效率或教育投入产出效率进行实证分析,鲜见深入分析教育投资与经济增长的脱钩关系及演化规律。葛涛和李金叶 [12] 通过比较全国西部地区、中部地区和东部地区城镇化和教育投入情况,发现西部地区随着城镇化的提升,教育投入对经济增长作用逐渐减弱;中部地区减弱程度降低,而对于东部地区而言,随着城镇化的提升,教育投入对经济增长作用具有非常显著的正效应;陈春平和胡何琼 [13] 通过对国民经济和高等教育的数据面板进行回归分析和灰色关联度分析,得出我国高等教育层次结构与经济发展显著相关的结论;赵庆年和曾浩泓 [14] 发现高等教育弹性系数对高等教育规模增长与经济发展间的关系变化的根本原因是高等教育系统对经济发展依赖性的降低及经济发展对高等教育依赖性的增强,揭示了高等教育与经济关系由低级走向高级的动态变化实质。在研究方法上,以往研究中多数学者主要采用单位根检验(ADF检验)、协整检验、Grander因果检验 [15] 、误差修正模型、VEC模型、DEA模型、系统GMM模型、主成分分析法、灰色关联度分析法、FEDER模型等方法研究教育投资与经济增长的相互关系,但鲜有从空间视域下采用空间自相关分析和脱钩指数方法研究教育结构与经济发展间的时空关联性。
2. 研究方法与数据说明
2.1. 样本选择及数据来源
本文数据主要包含1978年~2020年我国34个省市面板数据。但由于许多经济、政治、社会和环境特征数据在时间和地区维度上的缺失,因此原始数据是不平衡的面板数据。选取人民经济发展水平和教育支出能力分别作为本文两个主要的被解释变量和解释变量,由于其在1998年之前的数据缺失率高达95%。因此,本文研究的时间段为1998~2020年同时,为了保证在面板数据模型分析中数据的有用性,每个地区的数据量至少需要5个,所以删除不满足要求的地区数据样本(港澳台地区)。最终,获得由31个省市从1998~2020年所组成的基础数据集。
本文选取我国31个省市作为样本空间,研究时段为1998年至2020年,数据为面板数据。机器学习探索性分析、面板数据分析均使用该数据集。本文数据来源于1998年至2020年《中国统计年鉴》和国家统计局官网以及我国各省市统计年鉴,其中本文相关经济变量均使用当年价格。需要说明的是,由于需要收集的指标较多,通过多个统计报表获得的数据可能存在统计口径上的误差。
2.2. 变量筛选
影响一国人民经济发展水平的因素诸多,随着调查数据的逐渐积累,可用的控制变量也在逐渐增加。把不同的控制变量纳入模型中,虽有利于增加模型的解释力,但加入过多的控制变量则会降低模型的稳定性,甚至会出现模型结果的过度拟合。但不可忽略的是,已有文献中的控制变量选择大多是基于研究者的主观经验,为避免出现上述情况,本文使用机器学习中的随机森林方法来实现控制变量的精准筛选,既最大限度避免变量遗漏带来的内生性问题,又避免引入过多变量带来的潜在多重共线性问题。
本文在讨论教育支出能力对人民经济发展水平的影响机制过程中,发现数据集的范围和规模也为研究提供很多的控制变量选择。具体而言,初步筛选后的数据集每个省市包含1054个经济、政治、社会和环境等变量。本文通过采取如下选择流程实现控制变量的选取。第一,基于现有研究中所涉及的变量,初步整合得到1054个潜在的控制变量,再进一步剔除缺失程度超过5%的变量,最后潜在的控制变量还剩下232个;第二,在分析非平衡面板数据时,利用低方差滤波和高相关滤波过滤特征变量直至控制变量个数降低到187个;第三,利用随机森林通过基尼重要度来预测主变量。将已有数据集中获取的原始数据导入随机森林模型,通过数据挖掘进行分类分析,得到各个解释变量的重要程度。第四,对变量进行多重共线性检验进一步筛选变量,消除因参数估计的不确定性和回归分析中多重共线性而带来的问题。本文根据各控制变量对人民经济发展水平的贡献重要程度排序,选择与影响被解释变量(人民经济发展水平)的重要性程度最高的前20组变量作为控制变量的最优子集,见图1。其中涵盖了经济、社会和环境等方面的各种因素。进一步对20个变量进行多重共线性检验,结果显示所有变量在统计意义上皆不存在多重共线性问题。
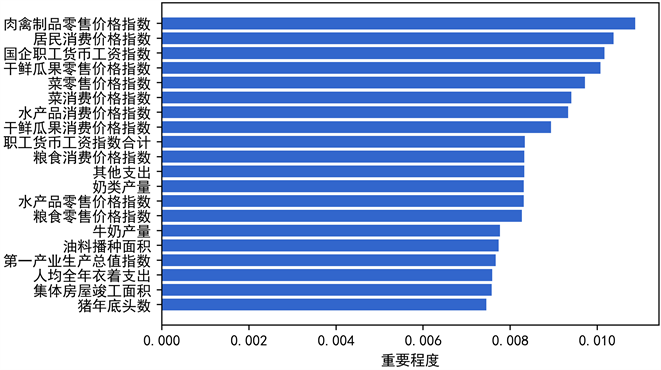
Figure 1. Feature importance of the top 20 control variables
图1. 前20个控制变量的特征重要程度
2.3. 变量描述
1) 被解释变量
由于人民经济发展水平这一指标在国家统计局官网以及统计年鉴中并未有直接数据,本文选取人均国内生产总值(Real GDP per capita)来代替人民经济发展水平的数据。人均GDP越高,说明人民购买力越强,该地区的人民经济发展水平越高。
2) 核心解释变量
本文的核心解释变量为教育支出程度。在本研究中,借鉴肖攀等 [16] ,同时通过规模和结构来反映:一是接受学校教育付出的费用,包括学杂费、书本费、文具费、食宿费、交通费等;二是接受校外教育付出的费用,包括补习班费、家教费、课外活动费等。本文以两类费用的金额总和来反映教育支出程度。
3) 控制变量
除了教育外,还有很多因素影响人民经济发展水平。基于1.2节筛选的贡献重要度排序的前20组控制变量,本文考虑从中提取居民消费价格指数、国企职工货币工资指数、粮食消费价格指数、其他支出、油料播种面积、地区生产总值指数(第一产业)、集体房屋竣工面积作为控制变量进行研究。具体指标说明见表1。

Table 1. Description of specific variables
表1. 具体变量说明
2.4. 研究思路
本文主要探究教育支出能力对人民经济发展水平的影响机制,教育支出是否能够使人民购买力提高等。本文在此基础上进一步验证教育支出的影响机制,在本文中,我们的研究思路具体如下:针对原始数据集进行特征降维,根据数据缺失情况、低方差(Var < 10)、高相关性(Corr > 0.8)进行变量的初步筛选;利用机器学习进行探索性分析,运用随机森林建模对控制变量进行贡献重要度排序,提取对人民经济发展水平贡献重要程度排名前20的特征,选取数据进行后续面板数据分析;从时间维度和空间维度对我国各省市人民经济发展水平的差异性进行分析,通过对变量进行多重检验,判断构建何种空间面板数据模型;构建空间权重矩阵,随后在空间权重矩阵的基础上进行空间自相关分析,其中包括全局自相关分析与局部自相关分析;针对教育支出能力对人民经济发展水平的影响程度,通过构建动态和静态面板数据模型,对影响我国各地区人民经济发展水平的多种因素进行分析。本文的研究思路图见图2。
3. 构建空间统计模型
3.1. 动态空间面板模型
3.1.1. 空间权重矩阵构建
经济发展水平会受到往期经济累积效应的影响,因此,需要考虑个体水平上的动态数据分析,采用动态模型。而当考虑到动态的因素时,首先就需要建立空间权重矩阵。
本文考虑选取用地理距离矩阵刻画空间权重矩阵,以各省份中心城市的经纬度为准,根据其经纬度计算出31个省份间的地理距离差,且矩阵中的非对角元素采用两城市间地理距离差的倒数:
(1)
由于空间权重矩阵是为了衡量空间因素,若两地区相邻越近,则说明该两个地区之间的空间因素可能影响更大,其对应的权重也就更大。对角线元素仍设置为0。
3.1.2. 全局空间自相关分析
全局空间自相关分析用于衡量各区域在整体上的空间差异和关联程度,通常使用Global Monran’s I统计量进行计量,即全局莫兰指数。其计算公式如下:
(2)
其中,
,n为空间单元总个数,
和
分别表示第i个空间单元和第j个空间单元的属性值, 为所有空间单元属性值的均值,
为空间权重值。
莫兰指数的取值通常在−1到1之间,莫兰指数接近于0时,则表明地区之间不存在空间相关性;莫兰指数接近1则表示区域具有相似属性,即高与高相邻、低与低相邻;莫兰指数接近−1则表示区域具有相异属性,即高与低相邻、低与高相邻 [17] 。
3.1.3. 局部空间自相关分析
局部空间自相关分析是一种用于衡量空间数据中局部区域间相关性的方法,与全局空间自相关分析类似。通过局部自相关分析可以有效检测由于空间相关性引起的空间差异,确定空间对象属性取值的热点区域或高发区域,并弥补全局自相关分析的不足。
其中局部空间自相关分析通常采用局部Moran’s I统计量来衡量,其计算表达式如下:
(3)
当局部Moran’s I统计量的值大于0时,则表示空间单元i与其邻近单元的属性相似;反之当局部Moran’s I统计量的值小于0时,则表示空间单元i与邻近单元的属性不相似。
4. 实证分析
4.1. 描述性统计分析
在进行构建具体的模型之前,往往需要对样本数据做相应的描述分析或探索分析,从而把握数据走向,充分了解数据所提供的信息,进而可以为建模分析提供良好的参考依据。各个变量的基本情况见表2。

Table 2. Descriptive statistics of variables
表2. 变量描述性统计
从表2中可以看出各变量的具体描述性统计信息,人均国内生产总值的最小值为2364元,最大值为164,889元,结果表明,不同省份的经济发展水平程度差异非常之大。教育支出的均值为2,631,317,说明我国目前的教育支出水平仍然处在较低水平。居民消费价格指数均值为102,说明平均来说我国居民的消费程度较高。根据表2所示,各个变量较为离散,其中只有居民价格消费指数这一变量数据分布较为集中。使得数据分布差异如此之大的原因,可能是时间变化的影响,也可能是地区之间的差异较大,但最有可能的情况是两者皆有。所以本文在进行后续建模分析时,把数据进行对数化处理,并以时间、空间作为落脚点,重点描述被解释变量与解释变量的时间变化和空间差异。
本文根据地理位置把31个省份分成东部地区、东北部地区、西部地区、东部地区这4个地区,探究每个省份教育支出与时间关系,见图3。
各省份教育支出逐年增加,中部地区和东北部地区这两个地区里的省份增长的比例比较一致,说明有较好的带动作用,由于西部地区和东部地区的各个省份实际情况复杂,教育支出增长比例不一致,尤以广东省增长最为迅速,西藏自治区、宁夏回族自治区、青海省、海南省这四个省份的教育支出增长比例最小,说明这四个省份对教育不够重视,本文认为教育支出比例增长越大,该地区经济发展水平越高,反之,地区经济发展水平不够高。
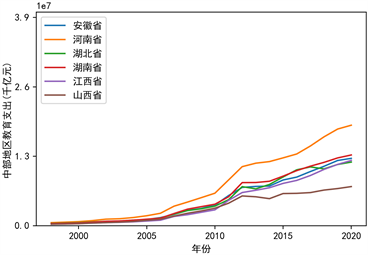
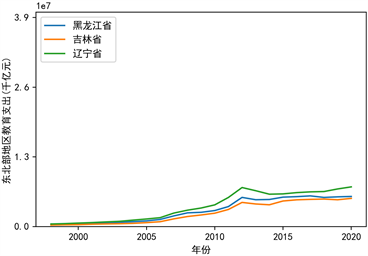
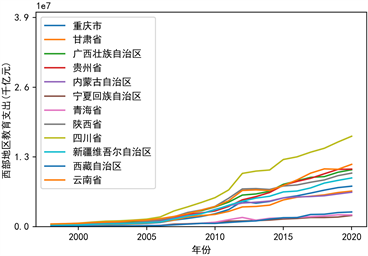
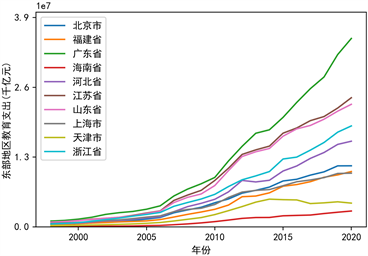
Figure 3. Expenditure on education by region
图3. 分地区教育支出情况
4.2. 静态面板数据模型
本文对变量进行平稳性探究,利用单位根检验(ADF)方法,在含截距项和趋势项的模型下,发现变量的原序列均不存在单位根过程,表明变量均处于平稳状态,检验结果见表3。

Table 3. Results of unit root test
表3. 单位根检验结果
从表3中可以看出,在给定0.05的显著性水平,包含截距项和趋势项的模型中,所有变量的ADF检验的P值都小于0.05,拒绝原假设,表明这些变量是平稳的时间序列数据。且由F检验可知,这些模型有相同的回归系数,但截距项不同,因此将模型设定为变截距模型。接下来,对模型进行Hausman检验以判断模型的固定效应和随机效应。检验结果见表4。
P值为2.316e−09,在0.05的显著性水平下,应该拒绝建立个体随机效应的原假设,即应该建立个体固定效应模型,结果见表5。

Table 5. Static panel data model estimation
表5. 静态面板数据模型估计
注:“***”、“**”、“*”分别表示在1%、5%、10%的水平下显著。
从模型整体的拟合效果来看,模型的R2= 0.9813,说明模型的解释力度很好。根据模型的回归结果得到以下回归方程:
从回归方程可知,教育支出的显著性水平非常高,增加100元的教育支出就会增加71元的GDP增长,某地区的教育支出增多,人民的受教育水平提高会推动该地区人口收入提升,从而使人均GDP增加、地区经济发展水平提高。
4.3 空间自相关性
4.3.1. 全局自相关
本文计算了我国31个省市2011年至2020年间人民经济发展水平的Moran’s I指数,结果见表6。
由表6可以看到,2011年至2020年间,我国各省市人民经济发展水平的Moran’s I指数均小于零,表明各省市的经济发展在空间上并非随机,而是有着负相关关系。且由于Moran’s I指数都比较接近0,所以经济发展水平在全局上体现了区域协同发展的整体思想。

Table 6. Moran’s I index by year
表6. 各年度Moran’s I指数
4.3.2. 局部自相关
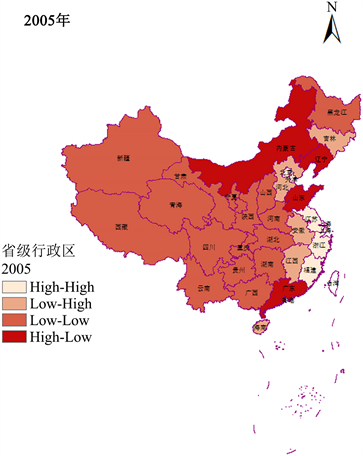
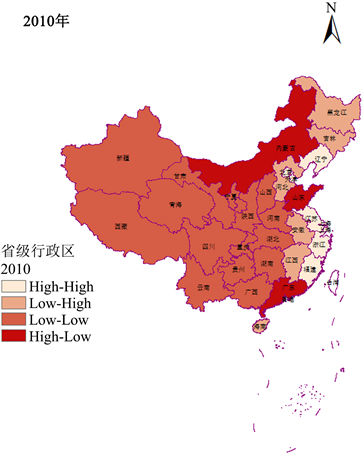
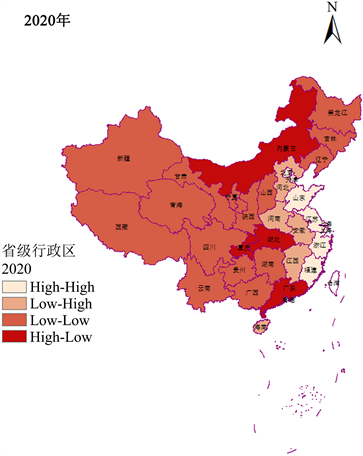
本节计算了我国2005年、2010年、2015年以及2020年间各省市的局域莫兰指数并绘制了LISA聚集图,并给出各地区局域莫兰指数所在象限结果,结果见图4和表7。
由图4我国人均GDP的LISA分布可以看出,整体上我国经济发展水平主要呈现出四种关系类型:“高–高”、“低–低”、“低–高”和“高–低”。“高–高”类型主要分布在我国沿海地区,“低–低”类型主要分布在我国中部以及西北地区。而“低–高”和“高–低”型集聚在我国南部、北部地区。可见我国沿海地区的经济发展水平进展相对较快。我国西北地区经济发展水平相对较低,可能和经济发展速度快、人口增速慢、区域资源整合较好等有关联。而我国中部、北部以及南部地区由于各省份市经济、社会、环境以及能源等方面发展不均衡,导致周边或相邻省份市之间的聚集状态呈现“低–高”或“高–低”型集聚。

 注:地图数据来自国家基础地理信息中心http://www.ngcc.cn/ngcc/。
注:地图数据来自国家基础地理信息中心http://www.ngcc.cn/ngcc/。
Figure 4. LISA diagram of local spatial autocorrelation of per capita GDP
图4. 人均GDP局部空间自相关LISA图

Table 7. Quadrant of local Monran’s I in each province of China
表7. 我国各省份局部Monran’s I所在象限
如表7所示,动态来看,2005年,江苏、浙江、福建、天津、上海、北京等地区呈现高–高聚集情况,具体表现为这些城市的人均GDP水平高于全国平均水平,意味着这些城市的经济发展水平高于全国平均水平,并且相邻城市的经济发展水平也高于全国平均水平。新疆、西藏、青海、甘肃和宁夏、黑龙江等地区呈现低–低聚集,具体体现在这些城市的人均GDP低于全国平均水平,且相邻城市的GDP也低于全国平均水平。2010年,高–高聚集区增加了辽宁省,而辽宁省由2005年的低–低聚集转向高–高聚集,五年来,辽宁省的社会、经济、环境等多方面发展速度较快。2015年我国各省份经济发展水平并未发生明显变化。2020年,山东、江苏、浙江、福建、天津、上海以及北京这7个省市呈现高–高聚集,湖北、广东、内蒙古以及重庆4个省市呈现低–低聚集,河南省由低–低聚集转向低–高聚集。
4.4. 动态面板数据模型
本文3.2节主要探讨了固定效应的线性静态模型,但是人民经济水平的发展发展不仅受当期影响,还受往期累积效应的影响,因此需要考虑个体水平上的动态模型。动态面板数据类型中,解释变量和上一期变量之间存在关系,上一期的值决定着下一期的值。
在建立动态空间面板模型后,对面板数据进行了LM检验,其中LM检验的P值为1.867,表明数据不存在序列自相关,于是考虑选择建立具有固定效应的空间滞后模型,并计算出模型的系数,结果见表8。

Table 8. Dynamic panel data model estimation
表8. 动态面板数据模型估计
注:“***”、“**”、“*”分别表示在1%、5%、10%的水平下显著。
从模型整体的拟合效果来看,模型的R2= 0.9890,说明模型的解释力度很好。根据模型的回归结果得到以下回归方程:
且从各个系数的回归结果来看,在给定0.05的显著性水平下,多数变量均通过了显著性检验。且该模型也通过了显著性检验。从估计的系数结果可以得出,教育支出、居民消费指数和地区生产总值指数的显著性水平相比其他变量而言较高,说明对人民经济发展水平影响较为显著的即为教育支出、居民价格消费指数、地区生产总值指数三个变量,且都是正影响,意味着,投入教育支出,会使得这个地区的GDP在近几年都会得到提高。
5. 结论
本文利用1998~2020年我国31个省份市的面板数据,构建了教育支出和经济发展水平指标,通过静态面板模型和动态面板数据模型,系统分析了教育支出对经济发展水平影响的作用机制,研究结果如下:
1) 不同省份的经济发展水平差异非常大。各省份的教育支出逐年增加,但增长比例各不相同。尤其是广东省的增长速度最快,而西藏自治区、宁夏回族自治区、青海省和海南省这四个省份的教育支出增长比例最小。这表明这四个省份对教育的重视程度不够。教育支出的增长比例越大,地区的经济发展水平就越高;相反,经济发展水平较低的地区教育支出增长不够。
2) 教育支出对经济水平的影响显著。当某个地区的教育支出增加时,人民的受教育水平提高,进而劳动人民的生产技能,推动人口收入的增加,从而提高人均GDP和地区的经济发展水平。
3) 在2011年至2020年期间,由于全局Moran’s I指数接近0,表明经济发展水平整体上体现了区域协同发展的思想。根据局部Moran’s I指数,我们可以观察到我国人均GDP的LISA分布呈现出四种关系类型:高–高、低–低、低–高和高–低。其中,“高–高”类型主要分布在我国沿海地区,“低–低”类型主要分布在我国中部和西北地区,而“低–高”和“高–低”型则集中在我国南部和北部地区。
4) 地区前一年的GDP对后一年的GDP有着正向的影响。对人民经济发展水平影响较为显著的因素包括教育支出、居民价格消费指数和地区生产总值指数等三个变量,且它们的影响都是正向的。
根据上述结论,为了提高教育水平,加强教育水平与经济耦合协调发展的程度,为推动人民经济发展水平提高,促进经济高质量发展,提出以下建议:
1) 重视教育发展:应重点关注教育水平的提升,加大教育支出,并加强教育政策的实施力度,以促进教育发展不受限制。特别是在西藏自治区、宁夏回族自治区、青海省和海南省等地,要加大力度推动教育事业的发展。
2) 提高教育投入:教育支出对经济水平的影响非常显著。各地应增加教育投入,培养更多人才,为人才提供更好的成长环境,提升劳动者的认知技能,从而提高劳动生产率,并促使他们留在本地区,进一步运用所学知识回馈本地区,推动经济发展。
3) 实现均衡发展:应推动四大城市群的均衡发展,适度引导人口向外围城市流动,缓解北上广深等大城市人口过大的压力,提升重庆、成都、武汉和长沙等城市的发展质量,加快成渝和长江中游地区等成熟型城市群的网络空间格局建设。同时,加强成熟型城市群核心城市的教育吸引力,促进教育与经济的协调发展。
4) 综合发展:各地区相互影响,并与去年的GDP密切相关。各地应紧抓机遇,不懈努力,产业结构的不断优化升级是经济增长的重要源泉之一。改善第一、二、三产业结构的发展也能有效促进经济发展。各地应保持整体发展的态势,注重协同合作,推动经济蓬勃发展。
参考文献
NOTES
*通讯作者。