P-M曲线计算异型桥墩正截面抗压承载力

期刊菜单

P-M曲线计算异型桥墩正截面抗压承载力
P-M Curve Calculation of the Normal Section Compressive Bearing Capacity of Special-Shaped Bridge Piers

DOI: 10.12677/HJCE.2023.128132, PDF, HTML, XML,
作者: 王升堂, 唐小清, 穆胜利：重庆路威土木工程设计有限公司，重庆；李兆阳：北京迈达斯技术有限公司，北京
关键词: P-M曲线；异型桥墩；正截面抗压承载力；P-M Curve； Irregular Pier； Normal Section Compressive Bearing Capacity

摘要: 伴随着经济高度的发展，人们对美的追求越来越高，桥梁的美不但体现在它的雄伟和魄力，更体现在它的细节，比如桥墩的形状设计等方面。城市桥梁中伴随城市快速的发展，城市桥梁不局限于采用一般的圆形墩矩形墩，更加广泛采用更具美感的花瓶墩。大型斜拉桥桥墩也广泛采用圆弧形造型等异型桥墩，公路、铁路桥墩也常采用圆端型桥墩，这些异型桥墩的抗压承载力计算成为设计者的一道难题。《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)中仅提供矩形、T型、I型和圆形截面的正截面抗压承载力计算公式，对于非标准形状的需要设计者进行截面等代后进行计算，对于设计者来讲增加了设计工作量，且等代形状后，后期处理存在差异。本文介绍采用P-M曲线结合《混凝土结构设计规范》(GB 50010-2010)计算异型桥墩正截面抗压承载力能力的方法。

Abstract: With the rapid economic development, people’s pursuit of beauty has reached new heights. The beauty of a bridge is not only reflected in its grandeur and boldness but also in its details, such as the design of the bridge piers. In urban areas, bridges are no longer limited to conventional circular or rectangular piers, but also widely adopt more aesthetically pleasing vase-like piers. Large cable-stayed bridges often feature unique pier shapes, like curved arcs, while highway and railway bridges frequently utilize cylindrical piers. However, the calculation of the compressive bearing capacity for these non-standard pier shapes poses a challenge for designers. The “Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts” (JTG 3362-2018) only provides calculation formulas for the normal section compressive bearing capacity of rectangular, T-shaped, I-shaped, and circular sections. For non-standard shapes, designers need to calculate the section after replacing it. This increases the design workload for designers, and there are differences in the later processing after replacing the shape. This article introduces the method of using the P-M curve combined with the “Code for Design of Concrete Structures” (GB 50010-2010) to calculate the compressive bearing capacity of the normal section of special-shaped bridge piers.

文章引用：王升堂, 李兆阳, 唐小清, 穆胜利. P-M曲线计算异型桥墩正截面抗压承载力[J]. 土木工程, 2023, 12(8): 1152-1160. https://doi.org/10.12677/HJCE.2023.128132

1. 引言

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)第5.3条 ‎[1] 的相关规定，矩形、T型、I型和圆形截面抗压承载力可以直接由规范公式计算得出，城市中为了美观采用了带槽的花瓶墩，花瓶墩的常用形式如下图1、图2所示：

Figure 1. Common forms of vase piers-1

图1. 花瓶墩常见形式1

Figure 2. Common forms of vase piers-2

图2. 花瓶墩常见形式2

如需采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)中相关公式进行抗压承载能力能力计算，花瓶桥墩的设计需要采用面积相等、抗弯惯性矩相等的原则，等效为矩形或I型截面，然而图2所示截面，很难等效为理想的矩形或I型截面，并且承受双向弯矩，双向偏压的结构也无法采用面积相等、抗弯惯性矩相的方法实现截面等效。根据《混凝土结构设计规范》(GB 50010-2010)附录E ‎[2] 的相关内容，为解决异型桥墩的正截面抗压承载力提供了一个如图3所示的解决方案：

$N \leq \sum_{i = 1}^{l} σ_{c i} A_{c i} - \sum_{j = 1}^{m} σ_{s j} A_{s j} - \sum_{k = 1}^{n} σ_{p k} A_{p k}$

$M_{x} \leq \sum_{i = 1}^{l} σ_{c i} A_{c i} x_{c i} - \sum_{j = 1}^{m} σ_{s j} A_{s j} x_{s j} - \sum_{k = 1}^{n} σ_{p k} A_{p k} x_{p k}$

$M_{y} \leq \sum_{i = 1}^{l} σ_{c i} A_{c i} y_{c i} - \sum_{j = 1}^{m} σ_{s j} A_{s j} y_{s j} - \sum_{k = 1}^{n} σ_{p k} A_{p k} y_{p k}$

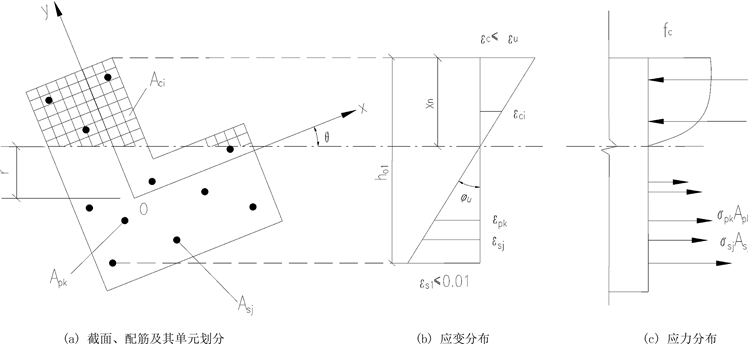
Figure 3. Calculation of the normal section bearing capacity of components with arbitrary cross sections

图3. 任意截面构件正截面承载力计算

2. P-M曲线简介

P-M曲线绘制：将截面离散为纤维模型，所有单元应变计算符合平截面假定，当受压侧混凝土单元达到极限压应变或受拉侧钢筋达到极限拉应变时，则认为该截面达到极限承载力，进而根据单元本构及应变计算单元应力，计算时根据单元面积及应力积分计算单元内力，最后将截面所有单元内力累加即可得到整个截面的极限承载力。P-M曲线绘制较为复杂，P-M曲线的绘制采用计算机编程详细绘制和计算 ‎[3] 。

P-M曲线描述了“拉压弯截面”的全部破坏状态，可以很好的阐述《混凝土结构设计规范》(GB 50010-2010)附录E中的计算任意截面正截面抗压强度的思路。曲线上任意一点表示截面在轴力和弯矩作用下的极限承载力。如图4中的P3点表示弯矩为零，仅受轴向力作用下的截面强度，即轴压承载力。M1点表示轴力为零，仅弯矩作用下的截面强度，即抗弯承载力。P1点表示弯矩为零，仅受轴向拉力作用下的截面强度，即轴拉承载力。而曲线的P3-Mmax段(图中绿色部分)表示截面的小偏心受压破坏，Mmax-M1段(图中紫色部分)表示大偏心受压破坏，M1-P1段(图中黄色部分)表示偏心受拉破坏。P-M曲线为截面特性计算得出，原则上适用于所有的截面形式 ‎[4] 。

Figure 4. P-M curve

图4. P-M曲线

3. P-M曲线工程实际运用

为了分析P-M曲线在实际工程中的实用性，我们分别对图1截面抗压强度分别按规范公式(等代截面方式)和P-M曲线计算进行比较，根据结果来判断P-M曲线在实际工程中的实用性。图1截面的等效矩形结果如表1所示：

Table 1. Comparison table of characteristics between section 1 and equivalent rectangular section

表1. 截面1与等效矩形截面特性比较表

从表1表格可以看出当截面承受X、Y双向弯矩的作用时候不能在面积相等、X、Y双向抗弯惯性矩相等的情况下完全等效。

图1截面采用C40混凝土，单侧受力主筋配置为HRB400直径22 mm钢筋16根，两侧共配置钢筋32根，钢筋距离受拉侧边缘0.05 m。

等效矩形截面在轴心荷载情况下根据公式进行计算：

$γ_{0} N_{d} \leq 0.9 φ (f_{c d} A + {f^{'}}_{c d} {A^{'}}_{s})$

P-M曲线采用Midas P-M曲线工具绘制及计算，曲线绘制结果：如图5及表2所示：

Figure 5. P-M curve calculation results

图5. P-M曲线结果

Table 2. P-M curve table calculation results

表2. P-M曲线表格结果

根据P-M曲线结果图5和表2的相关结论，查看M_x = 0时，P = 94,448.2 KN结果，与等效矩形截面(0.9倍轴压构件稳定系数暂定为1)正面抗压承载力的结果进行比较，如表3所示：

Table 3. Comparison table of normal section bearing capacity under axial load

表3. 轴心荷载下正截面承载力比较表

从表3可以看出，两种计算方法误差仅为0.24%，可见任意截面形状的轴心抗压强度可以采用P-M曲线计算得出，但如需根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018) ‎[1] 进行验算需要将P-M曲线的计算结果乘以0.9倍轴压构件稳定系数或将设计内力除以0.9倍轴压构件稳定系数 ‎[3] 。

以上结论在轴力作用下验证了P-M曲线的实用性，在弯矩和轴向力的共同作用下的结果差异情况将通过以下的对比得出。截面在弯矩和轴向力在表1所列数值的共同作用下采用《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018) (1)和(2)式进行相关的计算：

$γ_{0} N_{d} \leq f_{c d} b x + {f^{'}}_{s d} {A^{'}}_{s} + ({f^{'}}_{s d} - {σ^{'}}_{p 0}) {A^{'}}_{p} - σ_{s} A_{s} - σ_{p} A_{p}$ (1)

$γ_{0} N_{d} e \leq f_{c d} b x (h_{0} - \frac{x}{2}) + {f^{'}}_{s d} {A^{'}}_{s} (h_{0} - {a^{'}}_{s}) + ({f^{'}}_{p d} - {σ^{'}}_{p 0}) {A^{'}}_{p} (h_{0} - A_{p})$ (2)

公式(1)为采用轴力平衡的相关计算公式，根据(1)可以得到受压区面积和受压区高度，再根据(2)式进行弯矩的相关验算。规范公式(2)为对受拉侧钢筋取矩的验算结果，而P-M曲线计算采用对截面中心取矩的结果，如需要比较结果的一致性，首先运用截面内力矩平衡原理将公式(2)进行变形转换为对截面中心取矩的结果：

$γ_{0} N_{d} e^{'} \leq f_{c d} b x (\frac{h}{2} - \frac{x}{2}) + {f^{'}}_{s d} {A^{'}}_{s} (\frac{h}{2} - a^{'}) + f_{s d} A_{s} (\frac{h}{2} - a)$

计算时对等效矩形截面采用(1) ‎[1] 和(2)式 ‎[1] 变化式进行相关的计算，P-M曲线采用“保持P为常量”计算，输出结果如图6所示：

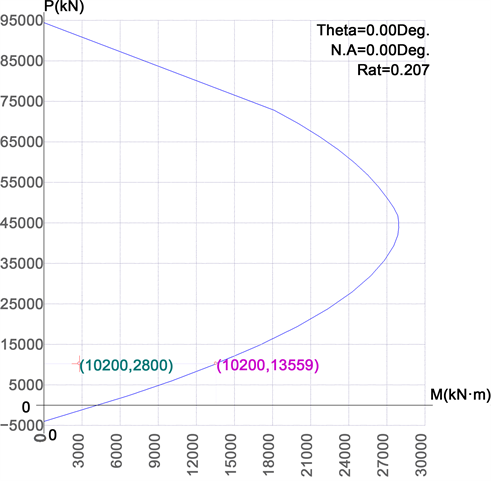
Figure 6. P-M curve (keeping P constant)

图6. P-M曲线(保持P为常量)

P-M曲线结果：保持P为常量，P = 10200KN时M = 13559 KN·m (承载力)；比较等效矩形截面采用规范计算方法与截面P-M曲线在轴力平衡时的计算结果如表4所示：

Table 4. Comparison of results between two methods for axial force balancing

表4. 轴力平衡时两种方法的结果比较

上述等效矩形截面采用规范法计算中因为内力对截面中心进行取矩，所以e'为ηe (η为偏心构件轴向力偏心距增大系数) ‎[1] ，不需要再累加中心距离受拉钢筋的距离： $\frac{h}{2} - a$ 。从表4结果可以看出，按照轴力平衡原理进行求解，P-M曲线计算能达到《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018) (2)式的验算结果，且精度较高。运用P-M曲线进行验算截面时仅需要将eη与P-M的抗力结果相比较，如设计弯矩结果小于抗力结果，则结构处于安全状态。

图6为轴力平衡时等到的相关结果，截面通过力矩平衡的相关计算，依然可以验证P-M曲线实用性。将截面对中心取矩公式变化为： $M_{d} \leq f_{c d} b x (\frac{h}{2} - \frac{x}{2}) + {f^{'}}_{s d} {A^{'}}_{s} (\frac{h}{2} - a^{'}) + f_{s d} A_{s} (\frac{h}{2} - a)$ ，通过力矩平衡求解受压区高度。为了计算简便先假定η = 1.0，则 $γ_{0} N_{d} e^{'} = M_{d}$ ，等效矩形截面按规范公式进行计算，P-M曲线采用“保持M为常量”计算，输出结果如图7所示：

Figure 7. P-M curve (keeping M constant)

图7. P-M曲线(保持M为常量)

P-M曲线结果：保持M为常量，M = 2800 KN·m时P = 91,107 KN (承载力)；等效矩形截面采用规范公式计算方法与截面P-M曲线在弯矩平衡时的计算结果如表5所示：

Table 5. Comparison of results between two methods for moment balancing

表5. 弯矩平衡时两种方法的结果比较

实际工程运用P-M曲线进行截面抗压承载能力验算时还需要将设计弯矩M_d考虑偏心构件轴向力偏心距增大系数η，通过考虑弯矩增大系数的P-M曲线结果与实际的N_d结果比较，得到结构是否安全的结果。

4. 结论

通过表3~5的相关结果可以看出，P-M曲线计算结果与规范方法计算结果的误差都在1%以内，可以得出P-M曲线计算结果在异型桥墩正截面抗压中的实用性。设计同行在异型桥型设计时可以合理的运用P-M曲线这个实用工具进行计算，也得出以下结论：

1) 将花瓶墩截面等效为矩形截面进行抗压承载力计算，截面特性较原截面有所改变；P-M曲线为纤维模型根据内力积分得到的曲线，计算机辅助计算，结果较为精确；两者在计算结果有差异，但两者计算结果差异在1%以内，可以运用于工程实际。

2) P-M曲线只与截面特性有关，可计算任意截面形状的正截面强度。

3) 采用轴力平衡和弯矩平衡，在规范公式变化下P-M曲线计算结果与规范公式计算结果基本一致。

4) 利用P-M曲线进行截面强度验算时，为了与《公路钢筋混凝土及预应力混凝土桥涵设计规范》 (JTG 3362-2018)匹配需要将设计内力值进行变化。

5) 在结构承受双向弯矩的作用下，比如横风区的桥墩，规范上尚无求解的相关公式，空间的P-M曲面可以很好的解决双向偏心的承载力计算。

参考文献

[1]	袁洪. 中华人民共和国交通运输行业标准. JTG3362-2018公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京: 人民交通出版社股份有限公司, 2018.
[2]	赵基达, 徐有邻, 等. 中华人民共和国国家标准. GB 50010- 2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
[3]	郭磊, 徐常泽. 任意截面P-M曲线绘制原理及其在强度验算中的应用[J]. 交通节能与环保, 2019, 15(2): 98-100.
[4]	叶见曙. 结构设计原理[M]. 第4版. 北京: 人民交通出版社股份有限公司, 2018: 164.

为你推荐

友情链接