1. 渐近线的定义
当曲线上一点沿曲线无限远离原点或者无限接近间断点时,如果该点到一条直线的距离无限趋近于零,那么这条直线就称为曲s线的渐近线 [1] 。函数图形描述的是“增减极值渐近线,凹凸拐点曲率圆 [2] ”,其中渐近线描述函数图形变化趋势。渐近线分为:垂直渐近线、水平渐近线、斜渐近线 [3] 。
1.1. 垂直渐近线
如果
,则
是函数
图形的垂直渐近线,也就是无穷间断点。
垂直渐近线可以有无数条,也就是有无数个无穷间断点,如
。
1.2. 水平渐近线
如果
,则
是函数
图形的水平渐近线。
求水平渐近线、斜渐近线需要针对函数关系
分别考虑两个单侧极限(
或
)。水平渐近线至多有两条(
或
)。
1.3. 斜渐近线
如果
,则
是函数
图形的斜渐近线。
斜渐近线也至多有两条(
或
)。
水平渐近线与斜渐近线总共最多有两条,不可能既是水平渐近线,同时又是斜渐近线。
根据
,求出
,
。
常规方法求渐近线都要求极限,因而做题难度偏大,尤其是求斜渐近线需求两次极限,难度最大。
隐函数
由于难以得出函数关系
,从而更加难以求出渐近线。
笔者通过多年教学实践总结出显函数
及隐函数
渐近线的快速简便方法——通过拆项及泰勒公式展开,然后利用极限与无穷小之间的关系即可求出,整个求渐近线过程避免求极限!
2. 求显函数
渐近线的快速简便方法
1) 求垂直渐近线就是找到函数
图形的无穷间断点
,也就求出了垂直渐近线
。
2) 求水平渐近线就是找到函数
,也就求出了水平渐近线
。
3) 求斜渐近线就是找到函数
,也就求出了斜渐近线
。
3. 显函数求渐近线实例
3.1. 简单题型
【例1】
的垂直渐近线为
(无穷间断点),水平渐近线为
。
【例2】 [5]
的垂直渐近线为
(无穷间断点),斜渐近线为
。
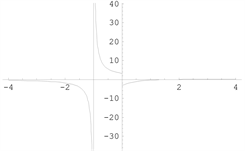
【例3】
的垂直渐近线
(无穷间断点),水平渐近线
。
函数图形如下图1。
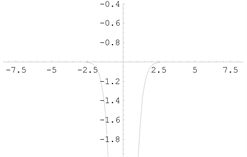
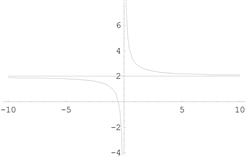 例1 例2 例3
例1 例2 例3
Figure 1. Graph of a function [4]
图1. 函数图形 [4]
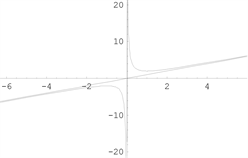
【例4】 [6]
,
,
,水平渐近线为
。
【例5】 [7]
,垂直渐近线为
(无穷间断点),水平渐近线为
。
【例6】 [8]
,垂直渐近线为
(无穷间断点),水平渐近线为
。
函数图形如下图2。
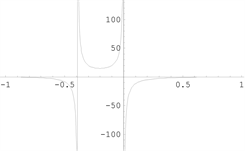
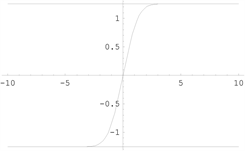 例4 例5 例6
例4 例5 例6
Figure 2. Graph of a function [4]
图2. 函数图形 [4]
3.2. 拆项题型
【例7】 [9]
,垂直渐近线为
(无穷间断点),水平渐近线为
。
【例8】
,垂直渐近线为
(无穷间断点),斜渐近线为
。
【例9】
,垂直渐近线为
(无穷间断点),斜渐近线为
。
【例10】
。
斜渐近线为
。
函数图形如下图3。

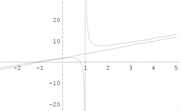
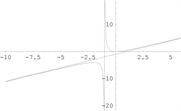
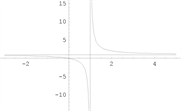 例7 例8例9 例10
例7 例8例9 例10
Figure 3. Graph of a function [4]
图3. 函数图形 [4]
【例11】
。
垂直渐近线为
(无穷间断点),水平渐近线
(
),斜渐近线为
(
)。
【例12】 [5]
。
垂直渐近线
(无穷间断点),水平渐近线
(
),斜渐近线
(
)。
【例13】 [9]
。
垂直渐近线
,
(无穷间断点),水平渐近线
(
),斜渐近线
(
)。
【例14】 [10]
垂直渐近线为
(无穷间断点),斜渐近线
。
函数图形如下图4。

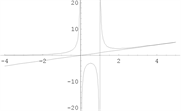
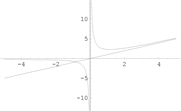
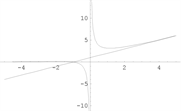 例11 例12 例13 例14
例11 例12 例13 例14
Figure 4. Graph of a function [4]
图4. 函数图形 [4]
3.3. 泰勒公式展开题型
【例15】 [11]
,水平渐近线
。
【例16】 [1]
,垂直渐近线为
(无穷间断点),斜渐近线为
。
【例17】 [12]
,垂直渐近线为
(无穷间断点),斜渐近线为
。
【例18】 [13]
,渐近线
函数图形如下图5。
【例19】(2020数二15分)曲线
(
)的斜渐近线。



 例15 例16 例17 例18
例15 例16 例17 例18
Figure 5. Graph of a function [4]
图5. 函数图形 [4]
。
这里:
,
,
,
,斜渐近线为
。
【例20】 [14]
垂直渐近线
(无穷间断点),渐近线
,
。
【例21】(2023数一5分)求
的渐近线。
解:垂直渐近线:
(无穷间断点),
(无穷间断点),
,
,斜渐近线:
【例22】 [11] 求
的渐近线。
解:
,垂直渐近线:
(无穷间断点)。
,
,
,
,
斜渐近线:
函数图形如下图6。


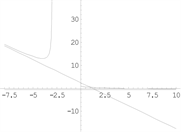
 例19 例20 例21例22
例19 例20 例21例22
Figure 6. Graph of a function [4]
图6. 函数图形 [4]
3.4. 等价无穷小替换题型
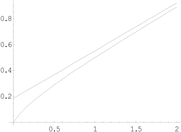
【例23】 [12]
.
时,
,
,
 时,
,
;
时,
,
;
时,一条斜渐近线为
;
时,另一条斜渐近线为
。
【例24】 [15] 求
的渐近线。
时,
,
;
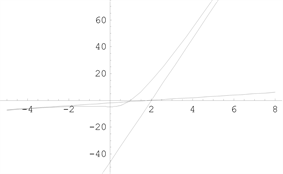 例23 例24
例23 例24
Figure 7. Graph of a function [4]
图7. 函数图形 [4]
时,
,
。
的斜渐近线为
函数图形如下图7。
4. 隐函数求渐近线
隐函数因函数关系
无法写出,只能通过隐函数方程
间接求渐近线。
4.1. 垂直渐近线
如果
,则
是隐函数
图形的垂直渐近线,也就是无穷间断点。
垂直渐近线可以有无数条,也就是有无数个无穷间断点。
4.2. 水平渐近线
如果
,则
是隐函数
图形的水平渐近线。
水平渐近线至多有两条(
或
)。
4.3. 斜渐近线
如果
存在,则隐函数
图形的斜渐近线
存在。
将
带入隐函数方程
求出b。
斜渐近线也至多有两条(
或
)。
4.4. 隐函数求渐近线实例
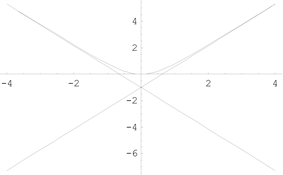
【例25】 [15] 求隐函数
的渐近线。
解:两边同除x、y最高次数x4、y3,得:
,
。
当
时,
,隐函数
图形的水平渐近线为
,
;
当
时,
,隐函数
图形的垂直渐近线为
。
,若
存在,则
时等式左边为
,
与右边为0矛盾,所以隐函数
没有斜渐近线。
【例26】 [15] 隐函数
,求渐近线。
解:
,水平渐近线
;
,垂直渐近线
;
,若
存在,则
时等式左边为
与右边为常数矛盾,
所以隐函数
没有斜渐近线。
【例27】 [16] 笛卡尔叶形线曲线
,
,
,则
时
,
。将
带入曲线方程
,得:
,
,
时,
,斜渐近线
。
常规求法:设
,则
,参数方程
当
时
,
,
,
,斜渐近线
。
函数图形如下图8。
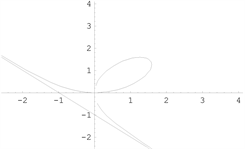
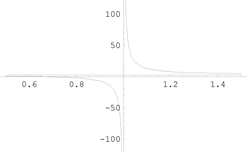
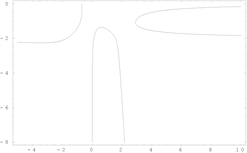 例25 例26 例27
例25 例26 例27
Figure 8. Graph of a function [4]
图8. 函数图形 [4]
本文中的所有图形均使用Mathematica 4.0绘制。
基金项目
《商务智能与大数据金融》建设项目(11511514002)。