1. 引言
永磁同步电机(Permanent Magnet Synchronous Motor, PMSM))运行可靠,结构简单广泛应用于电动汽车以及工业控制等领域 [1] [2] 。永磁同步电机的控制策略决定着驱动控制器的性能,矢量控制算法简单,但由于需要整定的参数限制了其在工程上的应用 [3] ,直接转矩控制结构简单稳态精度高,但不具备良好的动态响应,转矩脉动较大 [4] 。在众多先进的控制算法中,电流型模型预测控制由于其结构简单,易于实现,在非线性控制系统得到广泛的应用 [5] 。
目前对于电机的控制策略都是基于电机准确的数学模型发展而来,温度的升高,磁场的饱和会造成定子电感,永磁体磁链等电气参数的变化,但在工业控制中通常假定电机的参数不会发生变化这会使得整个系统的控制性能下降,因此需要通过在线辨识对电机的数学模型进行修正 [6] 。模型预测控制是一种基于电机准确数学模型的控制算法,其控制效果严重依赖于电机的准确参数。
电机的参数辨识分为离线辨识和在线辨识 [7] ,离线辨识只能在建立模型时进行,无法实时更新模型,因此无法适应系统运行中的变化。在线辨识是利用某种算法对获得的电机实际运行过程中的实时信息进行处理,得到待辨识参数的观察值,主要的在线辨识方法有:递归最小二乘法、模型参考自适应系统法、扩展卡尔曼滤波法和神经网络算法等。文献 [8] 对最小二乘法引入动态折息因子,通过估计误差对折息因子进行调整,克服了传统数据饱和与估计精度较差问题,但最小二乘法易于受到噪声的干扰从而影响辨识算法的精度。文献 [9] 设计了一组自适应率来进行参数辨识,首先辨识定子电阻、转子磁链,待两个参数辨识结果稳定后,再辨识直交轴电感。虽然在一个模型中实现多个参数辨识,但使得整个系统严重依赖于自适应率的设计,抗干扰能力较差。作为而神经网络算法具有较好的鲁棒性和较快的动态收敛速度但一般较为复杂且具有较大的计算量,不利于模型预测控制的在线寻优。文献 [10] 采用模型参考自适应对电机的永磁体磁链和电感进行辨识,并将结果用于无差拍电流预测控制中。扩展卡尔曼滤波算法是一种递归滤波算法,能够将测量值和模型预测值进行融合,从而提高参数辨识的精度和实时性 [11] 。扩展卡尔曼滤波算法进行参数辨识时输出矩阵会伴随输出电流预测值,与电流型模型预测控制相结合可以减少系统的计算时间。
本文将电流型模型预测控制和扩展卡尔曼滤波(Extended Kalman Filtering, EKF)算法相结合,提出了一种基于参数辨识的永磁同步电机预测控制策略。对电流型模型预测控制方程进行优化分析,结合电机数学模型的欠秩问题 [12] ,确认对模型预测影响较大的量来实现辨识算法对控制系统的在线修正。
2. 永磁同步电机的数学模型
在同步旋转d-q坐标系下,永磁同步电机的定子电压方程可以表示为:
(1)
(2)
式中:ud、uq为定子d轴和q轴电压;id、iq为定子d、q轴电流;Ld、Lq分别为定子d、q轴电感;R为定子电阻;ψf为转子磁链;ωe为转子电角速度。
3. 电流型模型预测控制
在永磁同步电机矢量控制系统中,PID控制策略由于结构简单,易于实现被广泛应用于电机伺服控制领域 [13] 。模型预测控制(MPC)省去了复杂的PID参数整定和SVPWM调制环节,通过选择合适的代价函数实时在线计算的方式选择最优的电压矢量。且结构简单、易于实现多个控制目标。模型预测控制可分为连续控制集模型预测控制和有限控制集模型预测控制 [14] 。有限控制集模型预测控制开关频率可变、无需调制器、设计结构简单、动态响应出色等特点 [15] 。因此本文采用电流型模型预测控制展开研究。如图1所示为模型预测控制的基本结构。

Figure 1. Basic process of model predictive control
图1. 模型预测控制的基本流程
自模型预测提出以来,越来越多的改进预测控制算法陆续出现,但他们都包含三个基本环节:预测模型、滚动优化和反馈校正 [16] 。如图2为永磁同步电机的模型预测控制的框图。
连续信号进行离散化处理,对(2)式进行一阶欧拉展开。
(3)
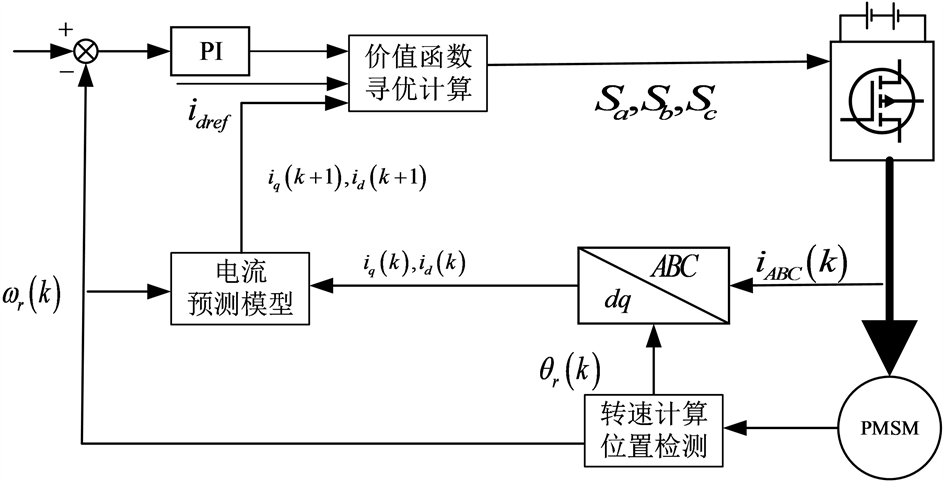
Figure 2. Model predictive control block diagram of permanent magnet synchronous motor
图2. 永磁同步电机模型预测控制框图
式中Ts为采样周期。
将式(3)代入式(2)整理得到永磁同步电机电流型模型预测控制方程:
(4)
在id= 0的控制方式下,通常选用d,q轴预测电流和参考电流之间误差的平方和作为代价函数。
(5)
式中iqref为定子电流q轴电流分量的参考值。
4. 电机参数的辨识
4.1. 温度及磁饱和对电机参数的影响
无论是传统的PI控制还是模型预测控制都是建立在电机的准确数学模型下,当电机参数准确时,预测控制的控制效果才能达到控制策略的最优控制性能。在设计电机的控制器时,通常是以离线辨识的电机参数为基础,在工作过程中都假设这些电机的参数不会发生变化的。这与实际的工况是不相符合的。
温度的变化是导致定子电阻和磁链变化的主要原因。不同定子绕组材料的电阻率与温度之间呈线性关系。
(6)
式中:RT为导体在温度T下的电阻值;R为绕组材料在常温T0下的电阻值;αT为绕组材料的电阻温度系数。
永磁体材料的磁性也受到温度的影响,对于不同的磁性材料温度带来的影响也不相同,如表1介绍了常见永磁材料的磁性能参数。
在一定温度范围内,永磁体材料的剩余磁通密度与温度之间呈现线性关系。
(7)

Table 1. Magnetic properties parameters of different permanent magnet mate
表1. 不同永磁体材料磁性能参数
式中BrT为永磁体材料在温度T下的剩余磁通密度,Br0为永磁体材料在温度为T0下的剩余磁通密度,α为永磁体材料的剩磁温度系数。
交直轴电感的大小与磁链的饱和程度相关,交直轴电流是导致磁链饱和的重要原因,一般认为交轴电感Lq的大小取决于q轴电流,直轴电感Ld的大小取决于d轴电流。而d轴电感和永磁体磁链处在同一方向,其本身处于较为饱和的状态受到d轴变化的影响比较小,q轴电流变化时q轴电感变化幅度较大 [17] 。
4.2. 单位基于扩展卡尔曼滤波的参数辨识
当永磁同步电机稳态运行时,定子电流d,q轴分量id,iq基本保持恒定。下一时刻的电流
近似等于id,
近似等于iq。由于采用id= 0的控制策略,在电机运行过程中电机定子电流d轴分量围绕着0附近小幅度波动,可以近似忽略。基于以上分析对式(4)进行改写:
(8)
可以明显地发现式(6)仅包含三个电机参数变量,定子电阻R,q轴电感Lq以及永磁体磁链。因为不包含d轴电感,可以近似的忽略d轴电感参数的变化对永磁同步电机控制产生的不良影响。同样的,在电机正常工作时,定子绕组产生的反电动势会平衡电源电压,这样定子电流在绕组上产生的压降较小,因此定子电阻的变化对整个控制系统的性能影响也会较小。在id= 0的电流型模型预测控制系统中对性能影响较大的因素是永磁体磁链ψf以及交轴电感Lq。对于表贴式永磁同步电机而言Lq= Ld。
与异步电机一样,永磁同步电机在整个电机控制系统实际运行过程中,工况的变化会导致电机的某些参数发生变化。这就使得预测模型中电机参数与电机模型实际参数间存在偏差,因此有必要对该问题进行深入的研究。本文采用EKF对电机参数进行在线辨识,并将辨识结果运用于电流模型预测控制。以表贴式永磁同步电机为例对扩展卡尔曼滤波算法进行介绍,为了方便计算,选择状态变量ψf和a = 1/L作为系统状态变量。
(9)
输出变量为:
(10)
整合得到系统的非线性方程:
(11)
对于状态空间的PMSM数学模型:
(12)
其中x为状态向量,y是输出向量,A是系统动态矩阵,B是输入矩阵,C是输出矩阵,D是直通矩阵。通过观察式1可以发现A不是常系数矩阵,输入矩阵B为0,直通矩阵D为0。可以得到以下形式的状态方程:
(13)
(14)
采用扩展卡尔曼滤波算法,需要对状态空间数学模型离散化考虑到系统模型存在误差引入零均值白噪声误差
,考虑到测量误差引入零均值白噪声
:
(15)
在扩展卡尔曼滤波算法的递推过程中,不是直接使用过程误差和测量误差,而是采用误差矢量的方差来衡量这两种误差的特性。
根据方差的定义得到协方差矩阵Q和M:
(16)
协方差矩阵Q和R有如下表达式
(17)
同样引入系统的协方差矩阵P,在永磁同步电机的实际运行过程中,系统模型存在的噪声和测量误差有着不可确定性,通过试凑法确认P、Q、M分别为:
(18)
扩展卡尔曼滤波算法包含预测阶段和校正阶段两个部分。第一部分对状态矢量进行预测,根据系统的动态数学模型,结合上一时刻的状态估计值来预测下一时刻的状态矢量,得到下一时刻的预测量对应的输出向量。
(19)
其中
(20)
式中带“~”表示为该变量预测值,带“^”表示为该变量估计值,Ts为采样周期。输出矩阵仅包含可测的id,iq。
第二部分更新误差预测值的协方差矩阵
(21)
F是状态转移矩阵
(22)
输入矩阵
:
(23)
通过以上计算可以得到
,
是一个4 × 4的方阵:
(24)
计算卡尔曼增益矩阵
(25)
对估计值进行更新
(26)
(27)
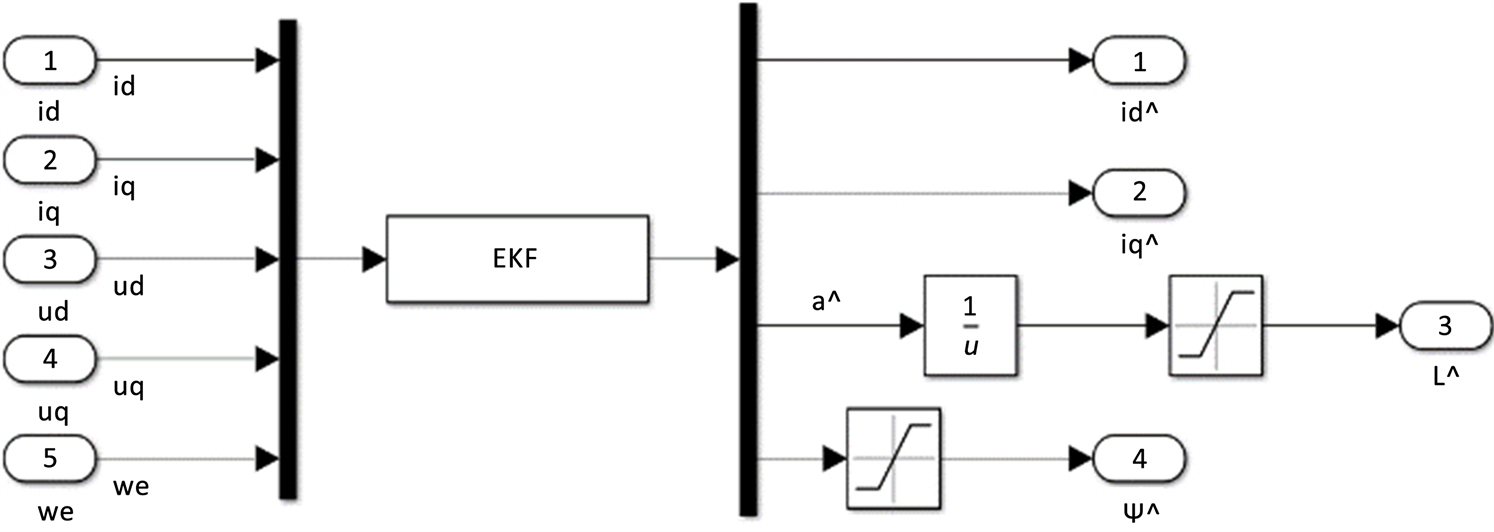
Figure 3. Model predictive control block diagram of permanent magnet synchronous motor
图3. 永磁同步电机模型性预测控制框图
这样整个EKF算法就完成了。通过对EFK算法的介绍,如图3所示为EKF算法的仿真实现。

Figure 4. Block diagram of predictive control for PMSM Based on parameter identification
图4. 基于参数辨识的PMSM预测控制框图
5. 仿真验证
本文提供的基于扩展卡尔曼滤波的永磁同步电机模型预测控制算法原理如图4所示。转速环采用PI控制策略,电流环采用电流型模型预测控制。将扩展卡尔曼滤波的辨识参数代入到模型预测控制中,使得控制器的参数与电机参数相匹配,根据图3在MATLAB/SIMULINK搭建仿真模型来验证控制算法。电机的各项参数如表2所示。

Table 2. Simulation parameters of PMSM
表2. 永磁同步电机仿真参数
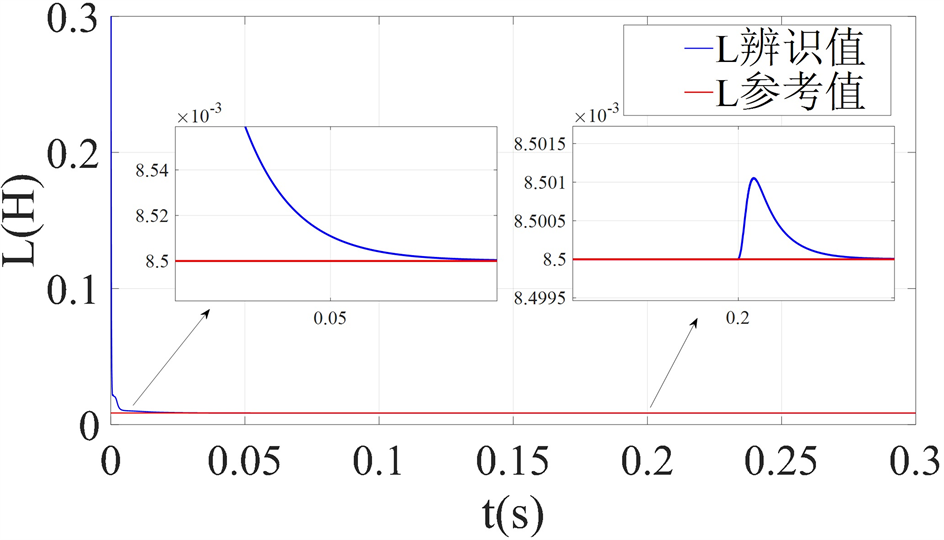
Figure 5. Identification value of stator inductance
图5. 定子电感的辨识值

Figure 6. Identification value of magnetic linkage
图6. 磁链的辨识值
在辨识过程中给定转速1000 r/min,逆变器的开关频率为10 kHz。在0.2 s时电机负载由5 N⋅m突变为10 N⋅m,如图5所示为定子电感的辨识值,图6为永磁体磁链的辨识值,从仿真结果中可以发现参数辨识结果的变化可以很快地收敛。
为了验证参数不匹配是否对电机预测控制产生不良影响,在仿真过程中对参数不匹配时的电机运行状况进行仿真验证得出d,q轴电流的参考波形。
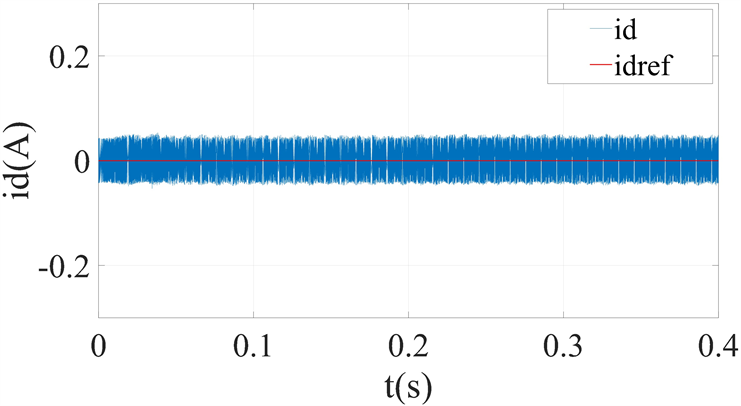
Figure 7. MPC simulation results with controller parameter misalignment underψf= 0.5ψf0; (a) q axis reference current and its response; (b) d axis reference current and its response
图7. 控制器在ψf= 0.5ψf0参数失配下MPC仿真结果;(a) q轴基准电流及其响应;(b) d轴基准电流及其响应
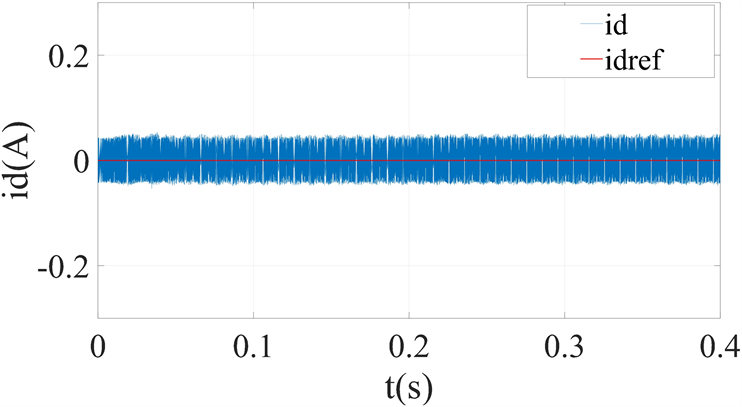
Figure 8. MPC simulation results with controller parameter misalignment underψf= 2ψf0; (a) q axis reference current and its response; (b) d axis reference current and its response
图8. 控制器在ψf= 2ψf0参数失配下MPC仿真结果;(a) q轴基准电流及其响应;(b) d轴基准电流及其响应

Figure 9. MPC simulation results with controller parameter misalignment underL=0.5 L; (a) q axis reference current and its response; (b) d axis reference current and its response
图9. 控制器在L =0.5 L参数失配下MPC仿真结果;(a) q轴基准电流及其响应;(b) d轴基准电流及其响应
假定在定子电感没有发生失配,而控制模型中永磁体磁链与实际值存在误差,在0.3 s时将MPC控制器中永磁体磁链参数设置为实际值的0.5倍和2倍如图7、图8所示。可以发现转子磁链失配前后d,q轴电流响应和脉动大小基本不变。控制模型中磁链为0.5倍时q轴参考电流有一个细微的抬升,控制模型中磁链为2倍时q轴参考电流有一个明显的下降,响应电流与参考电流之间存在静差。

Figure 10. MPC simulation results with controller parameter misalignment underL =2 L; (a) q axis reference current and its response; (b) d axis reference current and its response
图10. 控制器在L =2 L参数失调下MPC仿真结果;(a) q轴基准电流及其响应;(b) d轴基准电流及其响应
与永磁体磁链失配的仿真条件一致。控制器定子电感参数在0.3 s后发生失配如图9、图10所示。在从图9中可以发现q轴参考电流出现轻微下降,q轴响应电流与参考电流之间出现静差。从图10中可以发现,q轴响应电流脉动增大,这会导致转矩脉动的增大。q轴指令电流出现明显的抬升,但是响应电流没有出现抬升,这也会造成静差的增大,q轴电流的静差会影响到模型预测控制电流环的性能。

Figure 11.MPC simulation results based on parameter identification; (a) q axis reference current and its response; (b) d axis reference current and its response
图11. 基于参数辨识的MPC仿真结果;(a) q轴基准电流及其响应;(b) d轴基准电流及其响应
从图11可以看出,通过对电机定子电感和永磁体磁链的辨识,可以得到准确的数学模型,克服掉参数不匹配问题,从而可以使模型预测控制对电流进行准确的跟踪,克服掉参数扰动的影响,提高电流型模型预测控制的性能。
6. 结论
本文首先对电流型模型预测控制模型进行简化,结合永磁同步电机的欠秩情况合理的选择电机的待辨识参数,对于内置式永磁同步电机选择d轴电感Ld和磁链进行辨识,对于表贴式永磁同步电机选择电感L和磁链进行辨识。结合扩展卡尔曼滤波实现在线辨识的实时优化。从仿真结果中可以看出扩展卡尔曼滤波和电流型模型预测相结合,辨识效果能很好地对模型进行修正,减小id,iq的静态误差从而提高电流环的控制性能。