1. 引言
当前工业技术发展迅速,导致设备性能控制的门槛变得越来越高,同时电网与各种用电设备也对交流电电能的质量提出了更高要求。并且非线性负载的广泛应用导致大量谐波出现,对输出电压波形造成严重畸变,最终会影响到用电安全。以此为切入点进行研究,将非线性负载逆变电源作为主要研究对象,以智能化原理为主实现复合控制方法,对仿真以及样机实验进行分析,为逆变系统的优化工作提供理论、实验数据依据。结合模糊PI控制与BP神经网络控制的各自优点,采用了智能化的复合控制方法来提高系统的逆变波形质量 [1] 。
本文结合模糊PI控制与BP神经网络控制的各自优点,采用了智能化的复合控制方法来提高系统的逆变波形质量。模糊PI控制的优势在于可以在扰动或者畸变忽然出现时利用其参数自适应的能力,使其对PI参数迅速进行调整,达到使输出电压稳定的目的。BP神经网络控制技术的优势是具有非线性映射特性,可逼近不同类型的非线性变换,并且神经网络学习方式为训练,智能分析数学模型处理的数据取得相应结果。基于此设计复合控制系统,结合模糊PI控制以及BP神经网络控制的优势来对非线性问题以及不确定的控制问题进行深入研究。
通过MATLAB/SIMULINK仿真软件进行仿真,来验证该方法的正确性和有效性 [2] 。
2. 逆变器建模
在对逆变电路进行建模的过程中,选择负载电阻时,推算比较简单,情况较少,这并不能模拟出其在实际应用中的情况。在进行实际应用时,负载的类型会非常复杂,包括:线性、非线性、整流性等多种类型负载,所以在实际研究过程中我们并不能简单的用阻性负载数据作为其它负载进行使用 [3] 。为了进一步保证模型的稳定性,让其在附加不同类型负载时依旧不变化,本文通过等效电阻进行不同类型负载的模拟,如图1所示。
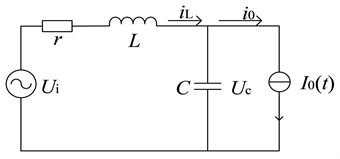
Figure 1. Circuit with arbitrary load topology
图1. 电路带任意负载拓扑图
建立如下状态方程:
电感电流iL和电容电压Uc为状态变量。
3. 模糊控制原理
模糊控制将人对非常复杂事物做出决策的过程形象化转变为机器语言,让计算机可以通过一系列的学习,模仿人在面对复杂事物时做出的决策,尤其是在对复杂程度非常高的数学模型构建时,合理的运用模糊规则将会在很大程度上减小工作量,从而实现对其进行更加精准有效的调整 [4] 。如图2为模糊PI控制器原理图。
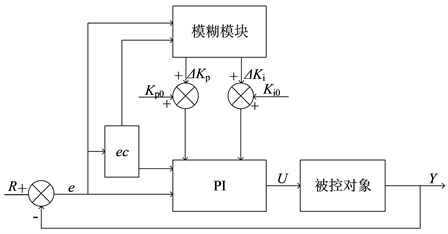
Figure 2. Fuzzy PI controller principle block diagram
图2. 模糊PI控制原理图
图3为Mamdani控制器原理图,包含知识库和模糊控制核心两部分,输入为偏差量e及其变化量ec,而在输出为单输出。
输入变量语句、输出变量的语句、隶属函数、模糊规则、模糊理论域范围、尺度变换因子等是模糊控制器最为核心的几个部分,也是设计过程的核心 [5] 。
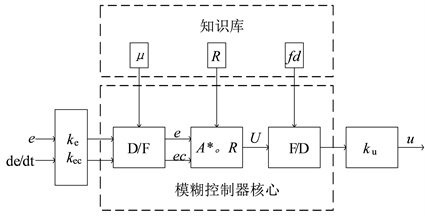
Figure 3. Mamdani controller schematic diagram
图3. Mamdani控制器原理框图
图3所示第一部分知识库中的
,R,fd,分别对应在离线情况下所得出的隶属函数、模糊规则以及清晰化算法,
存储将数字、模糊信号之间转变的的隶属度函数;R中存储控制器执行推算步骤要用到的算法还有条件语句;fd里面所贮存的是把模糊值向精确值进行转换时所用到的算法。第二部分模糊控制器核心框内的模块包括D/F,将精确值变换到模糊值所进行的运算;A*。R,类似于推理量,用来实现模糊量A*通过近似推理而得到模糊量U的过程;F/D实现将模糊量U变成清晰量的过程。为了进一步保证其输入和输出时的清晰度相互对应,还需要在D/F前添加ke、kec,在F/D后添加ku,其都被称为尺度变换因子 [6] 。
e以及ec所对应的理论域为:PB、PM、PS、Z、NS、NM、NB,按照所选择的控制规则,就可以得到下面这些条件词句:
(1) if e=PB and ec=PB then U=NB
(2) if e=PB and ec=PM then U=NB
(3) if e=PB and ec=PS then U=NB
(4) if e=PB and ec=Z then U=NB
(5) if e=PB and ec=NS then U=NM
(48) if e=NB and ec=NM then U=PB
(49) if e=NB and ec=NB then U=PB
根据上述的条件语句,得到表1来表示控制规则。

Table 1. Table of fuzzy control rules
表1. 模糊控制规则表
在MATLAB/Simulink搭建模糊控制器仿真模型。模型图如图4所示为模糊控制输入输出仿真图,图5为PI控制输入输出仿真图。

Figure 4. Input/Output simulation diagram of fuzzy control
图4. 模糊控制输入输出仿真图
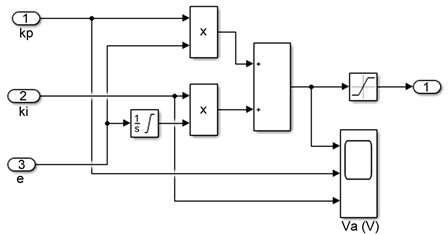
Figure 5. PI control input and output simulation diagram
图5. PI控制输入输出仿真图
4. 神经网络控制原理
传统控制方法在各个方面局限性颇多。但是神经网络控制拥有出色的自学能力以及无限逼近非线性变换的映射能力,用在非线性系统的识别、判断、控制中可以在很大程度上摆脱非线性模型的限制,明显优于传统方法。
并且神经网络是一种将人类大脑的思维过程数字化成数学模型的一种机器学习类型,它可以非常完美的模拟人脑的多项功能,但对于线性系统来说,该控制方法具有稳态特性和快速的动态响应。但是神经网络控制的鲁棒性较差,一旦系统参数出现较大波动或系统模型建立不准确时,系统将出现很强的震荡。因此以神经网络结合其他控制方法能够增加系统稳定性,防止因模型不准确导致的输出波形畸变 [7] 。
不同类型的神经网络可以通过模型组合以及算法组合进行混搭来构成,因此可以用于不同的需求。神经元是神经网络中的基础单元,神经网络是由一个个神经元连接而成,如图6所示为基础神经元 [8] 。
通过这个模型,可以把神经元当作多个输入、单个输出的非线性数据处理单位,若把神经元的输出量设为
,则有:
式中,
——神经元i的阈值;
——神经元j至神经元i的连接权值;
n——输入信号的数目;
——神经元输出;
t——时间;
——输出变换函数,一般情况下使用二进制或者s型函数进行表述,每种函数都有着非常不错的连续性和非线性等特点。
根据这个数学模型,对
和
两个变量进行调整从而实现对输出量大小的改变。
阈值函数型式为:
常规S形函数式为:
双曲正切函数式为:
双曲正切函数输出都属于正值,因此常用此函数代替传统S函数 [9] 。
5. 复合控制
非线性负载被使用的越来越普遍,单一的控制方法已经无法满足正常使用需求,采用多种控制方法成为了必然趋势,通过各个方法之间的优缺互补,构成具有更加完美性能的复合型控制器,使逆变电源输出电压的质量符合应用标准。本文选择模糊PI控制与BP神经网络控制技术相结合来组成复合控制,发挥两种控制方法的长处,优化非线性负载,验证理论准确性。

Figure 7. Block diagram of the compound control system
图7. 复合控制系统框图
复合控制器控制原理:在应用模糊规则进行模糊化和归一化的同时,将得到的数值在隶属函数中找出相应隶属度传递给神经网络,之后神经网络发挥自主学习功能,把模糊规则通过加强系数的模式体现出来,将模糊规则变换成加权系数对参数进行修正,最后输送给PI控制器来对被控对象进行控制,输出优化的值 [10] 。如图7所示。
复合控制器运行流程:通过神经网络的自主学习功能将模糊规则变换为加权系数来调整PID参数来实现优化。其中Fuzzy模块表示模糊PI控制,在BP神经网络中NN表示知识库,PID控制器是BP神经网络中的一部分,经过优化后的参数输送给被控对象,最后输出电压。
6. 仿真结果及结论
经过上述分析后,将在MATLAB平台搭建仿真模型对实验进行进一步的验证。仿真波形如图所示。
模糊控制波形图图8与神经网络控制输出波形图图9所示电压下降明显,无法达不到实验要求,并且模糊控制波形图波峰处有明显畸变,输出波形的精度不佳,谐波较多,而图10复合控制波形图,输出电压与参考电压重合,神经网络控制可以对模糊控制效果进行优化从而满足试验要求。
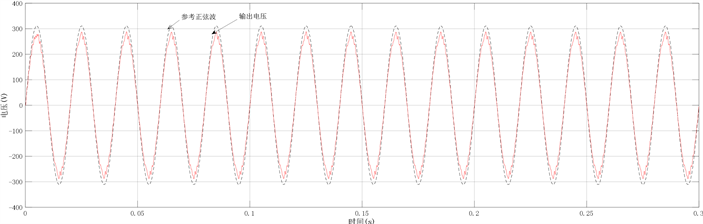
Figure 8. Fuzzy control output voltage waveform
图8. 模糊控制输出电压波形
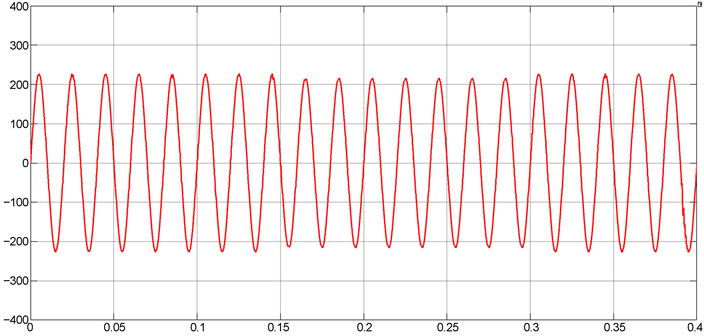
Figure 9. Neural network controls the output voltage waveform
图9. 神经网络控制输出电压波形
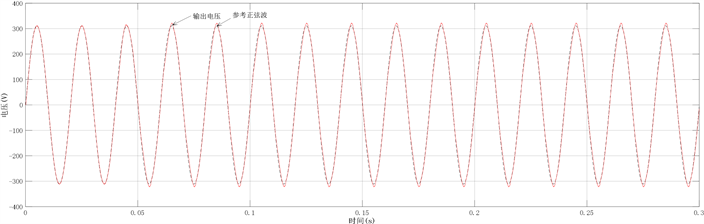
Figure 10. Compound control output voltage waveform
图10. 复合控制输出电压波形

Figure 11. Fuzzy control FFT analysis diagram
图11. 模糊控制FFT分析图

Figure 12. Neural network control FFT analysis diagram
图12. 神经网络控制FFT分析图

Figure 13. Composite control FFT analysis diagram
图13. 复合控制FFT分析图
图11单独施加模糊PI控制THD为6.13%,电压波形基本与标准正弦波接近一致,说明模糊控制由于其模糊化的特性,具有良好的动态反应能力,但是如图11FFT分析图所示,输出电压为264.8 V,电压下降较为明显,并不是逆变电源系统优化的最优解,因此单独控制的效果并不是最佳状态。图12输出THD值为2.49%可知BP神经网络PID控制基波电压波形更为平滑,畸变较小,但电压仅为219.4 V,并不能满足逆变电源的正常使用要求,因此单独控制的效果并不理想,图13所示为带整流性负载逆变电源输出电压THD分析图,电压畸变程度均稳定在3%以下,在良好状态甚至接近1%相较于单一控制器控制效果变化显著,电压THD符合实验要求。从输出电压FFT分析图可以得到THD仅仅只有1.25%这比起进行单独模糊控制状态下的6.13%、单独神经网络控制下的2.49%都是一个非常优的值,这说明本文提出的复合控制方法可以让THD值下降到一定程度,输出电能的质量得到优化。
对于复合控制控制器的响应不仅很快,而且波形整体畸变率很低,输出电压波形基本接近标准正弦波,说明将模糊控制与神经网络控制结合起来的复合控制比单独一种控制方法的效果更好。由THD分析可以明显看出,复合控制的总谐波畸变率比其他两种的明显降低,证明了该复合控制方法的可行性与有效性。
基金项目
国家自然科学基金(51777137)。