Al-4.8Mg合金热变形后的静态软化行为研究

期刊菜单

Al-4.8Mg合金热变形后的静态软化行为研究
Study on Static Softening Behavior of Al-4.8Mg Aluminum Alloy after Hot Deformation

DOI:10.12677/MS.2023.136066,PDF,HTML,XML,下载: 231浏览: 476科研立项经费支持
作者:戴青松,罗任,苏新,兰阳春：湖南湘投轻材科技股份有限公司，湖南湘西；曹柳絮：湖南湘投轻材科技股份有限公司，湖南湘西；中南大学粉末冶金研究院，湖南长沙
关键词:Al-4.8Mg合金；热变形；静态软化；静态再结晶动力学方程；br> Al-4.8Mg Aluminum Alloy；Hot De-formation；Static Softening；Kinetics Equation of Static Recrystallization

摘要:本文采用Gleeble热压缩模拟试验与金相检测，研究了Al-4.8Mg合金热变形后的静态软化行为。研究结果表明：Al-4.8Mg合金双道次热压缩过程中，材料经过第一道次热压缩及道次间停留后，第二道次流变应力相比第一道次呈现出阶梯状下降特征；提高第一道次的变形温度、应变速率、应变量及延长道次间隔时间，均可提升道次间静态再结晶程度，促进道次间的静态软化。根据实验结果建立了Al-4.8Mg合金的静态再结晶动力学方程，方程计算值与试验值的平均相对误差仅为3.8%。

Abstract:The static softening behavior of Al-4.8Mg alloy was examined after hot deformation using Gleeble thermal simulation experiment and metallography experiment in this work. Compared with the flow stress of Al-4.8Mg alloy in the first pass during the process of double pass hot compression, the flow stress of Al-4.8Mg alloy in the second pass was shown a step-like decline after the first pass hot compression and stop in the second pass. The static recrystallization degree between passes can be improved by increasing the deformation temperature, strain rate and strain variable of the first pass and extending the interval time between passes, thus promoting the static softening between passes. According to the experimental results, the static recrystallization kinetics equation of Al-4.8Mg alloy was established, and the average relative error was only 3.8% between the calculat-ed values and the experimental values.

文章引用：戴青松, 曹柳絮, 罗任, 苏新, 兰阳春. Al-4.8Mg合金热变形后的静态软化行为研究[J]. 材料科学, 2023, 13(6): 611-625. https://doi.org/10.12677/MS.2023.136066

1. 引言

Al-4.8Mg合金属于Al-Mg系合金，具有轻质、易成形、抗腐蚀等特征，且在生产与应用中具有独特优势，与Al-Cu、Al-Mg-Si、Al-Zn-Mg-Cu等热处理可强化铝合金相比，其生产过程不需进行固溶、淬火、时效等工序，而与纯铝、Al-Mn、Al-Fe-Si等热处理不可强化铝合金相比，该类合金具有更高的强度，因此，Al-Mg合金已成为各工业领域轻量化发展的重要材料，可广泛应用于交通运输、建筑装饰、食品包装、五金工装等领域 [1] [2] 。热连轧是制备材料的重要方式，Al-4.8Mg合金热连轧过程中的动态软化通常难以完全消除加工硬化，材料内部仍有部分组织处于高能不稳定状态，热变形后极易发生静态再回复、静态再结晶等组织演变，并形成静态软化 [3] [4] [5] [6] 。在热连轧生产中，静态软化对材料组织与性能调控非常重要，轧制道次间的静态软化可适当降低材料的加工硬化，改善金属塑性加工性能，而轧制完成后的静态软化更是直接影响到材料静态组织及性能调控。因此，研究Al-4.8Mg合金在热变形后的静态软化行为，并建立相关的材料指标预测模型，对设计材料成形工艺、调控成品组织与性能具有指导作用。本章将通过单、双道次热压缩试验，研究第一道次热变形参数及道次间隔时间对Al-4.8Mg合金热变形后静态软化行为的影响规律，构建材料静态再结晶动力学模型，为该合金热连轧后的静态组织及性能调控提供理论依据。

2. 实验方法

将已进行均匀化处理的Al-4.8Mg合金铸锭机加工成Φ10 × 15 mm的圆柱体试样，在Gleeble-3800热模拟机上采用单、双道次热压缩试验研究Al-4.8Mg合金热变形后的静态软化行为。压缩时试样两端添加石墨片并均匀涂上润滑剂(75%石墨 + 20%机油 + 5%硝酸三甲苯脂)以减小摩擦的影响，加热速度为10℃/s，加热至目标温度后保温3 min，确保试样温度均匀。

双道次热压缩工艺参数如表1所示，热压缩过程控制工艺如图1(a)所示，利用双道次热压缩的流变应力数据，研究第一道次热压缩参数及道次间隔时间与静态软化程度的定量关系。单道次热压缩工艺参数如表2所示，热压缩过程控制工艺如图1(b)所示，对“单道次热压缩 + 保温”处理的试样进行金相组织检测，研究热压缩参数及保温(间隔)时间对材料热变形后微观组织的影响。结合应变应力曲线与微观组织构建Al-4.8Mg合金的静态再结晶动力学模型。

Table 1. Parameters of two-pass hot compression tests for static softening behavior

表1. 基于静态软化行为研究的双道次热压缩工艺参数

Table 2. Parameters of single-pass hot compression tests for static softening behavior

表2. 基于静态软化行为研究的单道次热压缩工艺参数

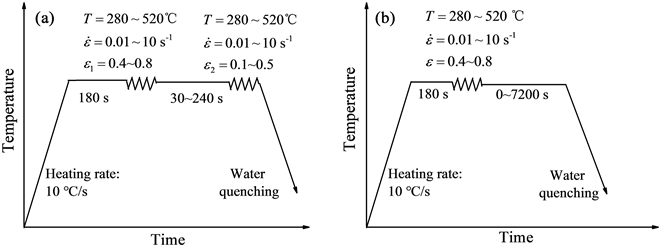
Figure 1. Process routes of hot compression tests for static softening behavior: (a) two-pass; (b) single-pass

图1. 基于静态软化行为研究的热压缩试验工艺路线：(a)双道次；(b)单道次

3. 实验结果与分析

3.1. Al-4.8Mg合金双道次热压缩过程中的宏观流变应力特征

当热压缩应变速率 $\dot{ε} = 1 s^{- 1}$ 、第一道次应变量 $ε_{1} = 0.6$ 、第二道次应变量 $ε_{2} = 0.3$ 时，Al-4.8Mg合金在不同变形温度及不同道次间隔时间下的双道次热压缩流变应力曲线如图2所示。从图可知，材料经过热变形后的道次间停留后，第二道次流变应力呈现出不同程度的阶梯状下降特征，且间隔时间越长，第二道次流变应力下降越大。这是因为材料热变形后在道次间隔期间会发生静态回复、静态再结晶等组织演变，形成了软化效应，流变应力下降，道次间隔时间越长，则静态软化越充分，流变应力下降程度越大。对比图2(a)~(e)可知，在同等道次间隔时间下，随着第一道次变形温度的提升，第二道次应力下降程度增大。如图2(a)所示，T= 280℃时第一道次峰值应力为194.6 MPa，间隔120 s后第二道的峰值应力降至188.6 MPa，峰值应力下降了3.1%；而当T= 520℃时，如图2(e)所示，间隔120 s后峰值应力从第一道次的64.8 MPa下降至第二道的45.9 MPa，下降程度接近30%。

图3为T= 400℃、 $ε_{1} = 0.6$ 、 $ε_{2} = 0.3$ 时，Al-4.8Mg合金在不同应变速率及不同道次间隔时间下的双道次热压缩流变应力曲线。在同等道次间隔时间下，随着应变速率的提升，第二道次流变应力下降程度增大。以道次间间隔时间240 s为例，由图3(a)可知，当 $\dot{ε} = 0.01 s^{- 1}$ 时第一、二道次的峰值应力分别为62.9 MPa、57.0 MPa，峰值应力下降9.4%；当 $\dot{ε} = 10 s^{- 1}$ 时，图3(c)中第一、二道次峰值应力分别为148.4 MPa、117.3 MPa，峰值应力下降超过20%。

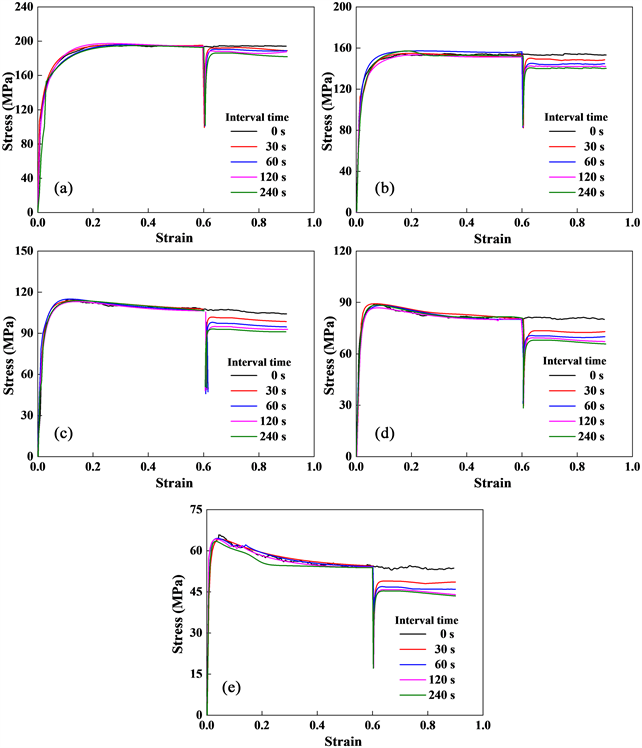
Figure 2. Flow stress curves of Al-4.8Mg alloy in two-pass hot compression under different temperatures ( $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ): (a) 280˚C; (b) 340˚C; (c) 400˚C; (d) 460˚C; (e) 520˚C

图2. Al-4.8Mg合金在不同变形温度下的双道次热压缩流变应力曲线( $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ )：(a) 280˚C；(b) 340˚C；(c) 400˚C；(d) 460˚C；(e) 520˚C

当T= 400℃、 $\dot{ε} = 1 s^{- 1}$ 时，Al-4.8Mg合金在不同应变量及不同间隔时间下的双道次热压缩流变应力曲线如图4所示。在同等道次间隔时间下，第一道次应变量增大后，第二道次流变应力下降程度提高。以间隔240 s为例，当 $ε_{1} = 0.4$ 时，图4(a)中的峰值应力从第一道次114.8 MPa降至第二道次97 MPa，降幅15.5%；当 $ε_{1} = 0.6$ 时，图4(b)中第二道次峰值应力降至90.2 MPa，降幅达到24.6%。

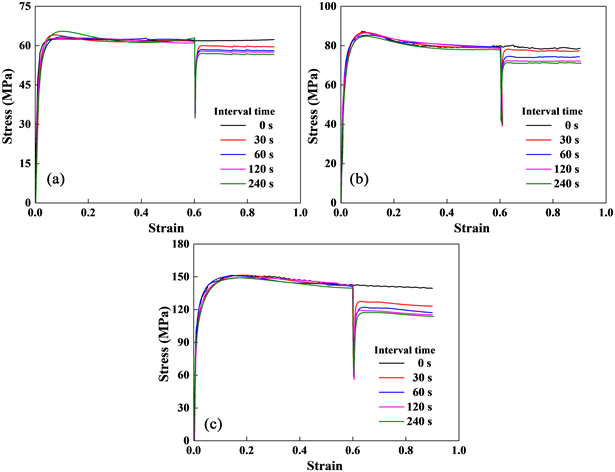
Figure 3. Flow stress curves of Al-4.8Mg alloy in two-pass hot compression under different strain rates (T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ): (a) 0.01 s⁻¹; (b) 0.1 s⁻¹; (c) 10 s⁻¹

图3. Al-4.8Mg合金在不同应变速率下的双道次热压缩流变应力曲线(T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ): (a) 0.01 s⁻¹；(b) 0.1 s⁻¹；(c) 10 s⁻¹

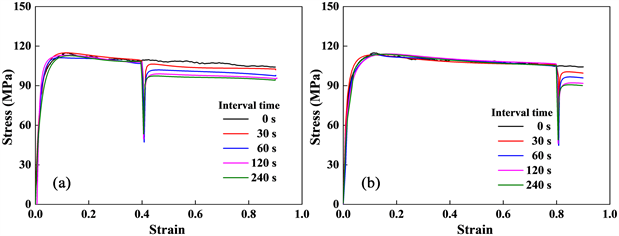
Figure 4. Flow stress curves of Al-4.8Mg alloy in two-pass hot compression under different strains (T= 400˚C, $\dot{ε} = 1 s^{- 1}$ ): (a) $ε_{1} = 0.4$ , $ε_{2} = 0.5$ ; (b) $ε_{1} = 0.8$ , $ε_{2} = 0.1$

图4. Al-4.8Mg合金在不同应变量下的双道次热压缩流变应力曲线(T= 400˚C， $\dot{ε} = 1 s^{- 1}$ ): (a) $ε_{1} = 0.4$ ， $ε_{2} = 0.5$ ；(b) $ε_{1} = 0.8$ ， $ε_{2} = 0.1$

可见，Al-4.8Mg合金双道次热压缩过程中，提高第一道次的变形温度、应变速率、应变量及延长道次间隔时间，均可促进道次间的静态软化，并导致第二道次流变应力的下降程度增大。

3.2. Al-4.8Mg合金双道次热压缩道次间的微观组织演变规律

当 $\dot{ε} = 1 s^{- 1}$ 、 $ε_{1} = 0.6$ 时，Al-4.8Mg合金经不同温度热压缩及热压缩后保温时间t= 240 s的金相照片如图5所示。在T= 280℃下，难以观察到试样的动态再结晶现象(图5(a))，热压缩试样间隔240后，在

Figure 5. Effects of compression temperatures on microstructures of Al-4.8Mg alloy ( $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ ): (a)T= 280˚C,t= 0; (b)T= 280˚C,t= 240 s; (c)T= 400˚C,t= 0; (d)T= 400˚C,t= 240 s; (e)T= 520˚C,t= 0; (f)T= 520˚C,t= 240 s

图5. 热压缩温度对Al-4.8Mg合金微观组织的影响( $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ): (a)T= 280˚C，t= 0；(b)T= 280˚C，t= 240 s；(c)T= 400˚C，t= 0；(d)T= 400˚C，t= 240 s；(e)T= 520˚C，t= 0；(f)T= 520˚C，t= 240 s

图5(b)中依旧难以观察到明显再结晶现象。当T= 400℃时，图4~图5(c)中晶界处可观察到细小动态再结晶晶粒，间隔240 s后再结晶晶粒明显增多(图5(d))。当温度达到520℃时，如图5(e)与图5(f)所示，试样变形过程中及间隔240 s后的再结晶程度都明显提高。金相照片说明提高热变形温度不仅可促进材料热变形过程中的动态再结晶，同时也会提升热变形后的再结晶程度。在热变形过程中，提高变形温度可使材料内部形成更多高能不稳定组织，热变形后尚未长大的动态再结晶晶核能继续吸收能量并迅速发生亚动态再结晶。同时，材料在道次间隔期间吸收能量后，新的晶核在晶界、亚晶界处形成，并长大成静态再结晶晶粒。

图6为T= 400℃、 $ε_{1} = 0.6$ 条件下Al-4.8Mg合金经不同速率热压缩及热压缩后间隔240 s的金相照片。由图6(a)可知，当 $\dot{ε} = 0.01 s^{- 1}$ 时，材料热压缩过程中未发生动态再结晶，在400℃下间隔240 s后金相照片中已可观察到细小再结晶晶粒(图6(b))。当 $\dot{ε} = 10 s^{- 1}$ 时，图6(c)中的动态再结晶晶粒清晰可见，间隔240 s后再结晶晶粒明显增多(图6(d))。通过对比可知，较高的应变速率不仅容易引发动态再结晶，同时也可促进静态再结晶的发生。热变形过程中，应变速率越高，变形时间越短，热变形积累的能量来不及释放，当能量达到一定程度时将诱发动态再结晶，由于热变形不均匀，亚晶能量分布不均，虽然部分亚晶通过动态再结晶释放了能量，但依旧有大量亚晶处于高能不稳定状态，在道次间隔期间能够迅速吸收能量引发静态再结晶。因此提高应变速率不仅有利于材料发生动态再结晶，同时也促进了材料在热变形后的静态再结晶。

Figure 6. Effects of compression strain rates on microstructures of Al-4.8Mg alloy (T= 400˚C, $ε_{1} = 0.6$ ): (a) $\dot{ε} = 0.01 s^{- 1}$ ,t= 0; (b) $\dot{ε} = 0.01 s^{- 1}$ ,t= 240 s; (c) $\dot{ε} = 10 s^{- 1}$ ,t= 0; (d) $\dot{ε} = 10 s^{- 1}$ ,t= 240 s

图6. 热压缩速率对Al-4.8Mg合金微观组织的影响(T= 400˚C， $ε_{1} = 0.6$ )：(a) $\dot{ε} = 0.01 s^{- 1}$ ，t= 0；(b) $\dot{ε} = 0.01 s^{- 1}$ ，t= 240 s；(c) $\dot{ε} = 10 s^{- 1}$ ，t= 0；(d) $\dot{ε} = 10 s^{- 1}$ ，t= 240 s

图7(a)是Al-4.8Mg合金在T= 400℃、 $\dot{ε} = 1 s^{- 1}$ 条件下热压缩应变量达到0.4时的金相照片，可见原始晶界处已形成了动态再结晶晶粒。当热压缩后间隔240 s，图7(b)中静态再结晶晶粒清晰可见。当应变量提高到0.8时，图7(c)中原始铸态晶粒被压扁，变形程度明显提升，且晶界处的动态再结晶晶粒数量增加，间隔240 s后晶界处分布了大量再结晶晶粒(图7(d))。材料变形程度增大有利于变形能积累，并优先发生动态再结晶，因此试样在应变量为0.8时其内部积累的能量更高，变形过程中达到动态再结晶临界能量的区域将发生动态再结晶，而能量接近临界值的区域在热变形完成后可快速吸收能量，并引发再结晶，因此，应变量为0.8的试样保温后再结晶程度更高。由此可见，当增大材料热变形量时，材料无论是热变形过程中的动态再结晶还是热变形后的静态再结晶程度均得到提升，再结晶组织势必带来更加明显的材料力学软化效果，因此，图4中在同等道次间隔时间下，第一道次应变量增大后，第二道次流变应力下降程度提高。

Figure 7. Effects of compression strains on microstructures of Al-4.8Mg alloy (T= 400˚C, $\dot{ε} = 1 s^{- 1}$ ): (a) $ε_{1} = 0.4$ ,t= 0; (b) $ε_{1} = 0.4$ ,t= 240 s;(c) $ε_{1} = 0.8$ ,t= 0; (d) $ε_{1} = 0.8$ ,t= 240 s

图7. 热压缩应变量对Al-4.8Mg合金微观组织的影响(T= 400˚C， $\dot{ε} = 1 s^{- 1}$ )：(a) $ε_{1} = 0.4$ ，t= 0；(b) $ε_{1} = 0.4$ ，t= 240 s；(c) $ε_{1} = 0.8$ ，t= 0；(d) $ε_{1} = 0.8$ ，t= 240 s

图8为T= 400℃、 $\dot{ε} = 1 s^{- 1}$ 、 $ε_{1} = 0.6$ 条件下，Al-4.8Mg合金热压缩后保温不同时间后的金相照片。从图5(c)可知，试样热压缩过程中已发生动态再结晶，间隔120 s再结晶程度增大(图8(a))，随着间隔时间的延长，再结晶程度不断提高。对比图8(b)与图8(c)可知，当间隔时间达到600 s 时再结晶基本完成，继续延长时间对再结晶程度影响较小。将间隔时间延长至7200 s时，如图8(d)所示，再结晶晶粒尺寸稍有变大，但不存在数量级差别。材料热变形后其内部存在大量高能不稳定的组织，道次间隔期间能够吸收能量并引发再结晶，保温时间越长则能量吸收越多，组织演变越充分。但随着再结晶过程中位错密度的降低及变形能的逐步消耗，微观组织演变的驱动力逐步下降，再结晶趋于稳定。材料长期处于保温状态时，晶界能可能发生变化并引起晶粒长大。

Figure 8. Effects of interval time on microstructures of Al-4.8Mg alloy (T= 400˚C, $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ ): (a)t= 120; (b)t= 600 s; (c)t= 3600 s; (d)t= 7200 s

图8. 道次间隔时间对Al-4.8Mg合金微观组织的影响(T= 400˚C， $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ )：(a)t= 120；(b)t= 600 s；(c)t= 3600 s；(d)t= 7200 s

3.3. Al-4.8Mg合金静态再结晶动力学模型

3.3.1. Al-4.8Mg合金静态软化率

根据Al-4.8Mg合金的双道次热压缩流变应力曲线可知，材料道次间发生的静态软化对第二道次流变应力影响显著。通常采用式(1)所示的力学软化法对材料静态软化程度进行定量分析 [7] 。

$F_{s} = \frac{σ_{1 s} - σ_{20}}{σ_{1 s} - σ_{10}}$ (1)

式中：F_s为静态软化率， $σ_{1 s}$ 为第一道次热压缩卸载时的应力， $σ_{10}$ 为第一道次热压缩变形中的屈服应力， $σ_{20}$ 为第二道次热压缩变形中的屈服应力。当F_s= 0%时，说明材料在道次间没有任何软化现象发生；当F_s= 100%时，说明材料在道次间发生了完全再结晶，加工硬化被完全消除；当F_s处于0~100%时，加工硬化得到部分消除。

图9为双道次热压缩道次间静态软化率F_s与第一道次变形参数间的关系。如图9(a)所示，当第一道次应变速率 $\dot{ε} = 1 s^{- 1}$ 、应变量 $ε_{1} = 0.6$ 时，静态软化率F_s随着热变形温度的提升而增大。如在第一道次热压缩变形温度为280℃的条件下，变形后间隔时间t= 240 s时，静态软化率F_s= 28.8%；同等间隔时间下，当温度提高至400℃时，F_s达到66.2%；而在变形温度为520℃的条件下，F_s已升至95.4%。对比图9(b)中的数据可知，当第一道次变形温度T= 400℃、应变量 $ε_{1} = 0.6$ 时，在同等间隔时间下，静态软化率F_s随着第一道次应变速率的提高而增大。图9(c)为T= 400℃、 $\dot{ε} = 1 s^{- 1}$ 条件下，第一道次应变量分别为0.4、0.6及0.8时，材料在热变形后不同间隔时间下的静态软化率，显然，增大第一道次应变量可提高道次间的静态软化率。当 $ε_{1} = 0.4$ 时，间隔120 s后F_s= 36.8%，同等条件下 $ε_{1} = 0.8$ 时F_s已升至56.9%。此外，通过图9可发现，随着热变形后间隔时间的延长，材料静态软化率F_s在快速上升后有逐渐趋于平稳的变化趋势，即静态软化率的增大速度逐步降低。以T= 400℃、 $\dot{ε} = 1 s^{- 1}$ 、 $ε_{1} = 0.6$ 的变形条件为例，如图9(b)所示，间隔时间为60 s时F_s为33.7%，间隔时间为240 s时F_s为47.1%，材料的静态软化在前60 s内就已完成了一半以上，说明静态软化率增大速率逐步降低。可见，提高第一道次变形温度、应变速率、应变量及延长道次间隔时间，均可提升材料在道次间的静态软化率，但随着道次间隔时间的延长，静态软化率的增大速度逐步变缓。

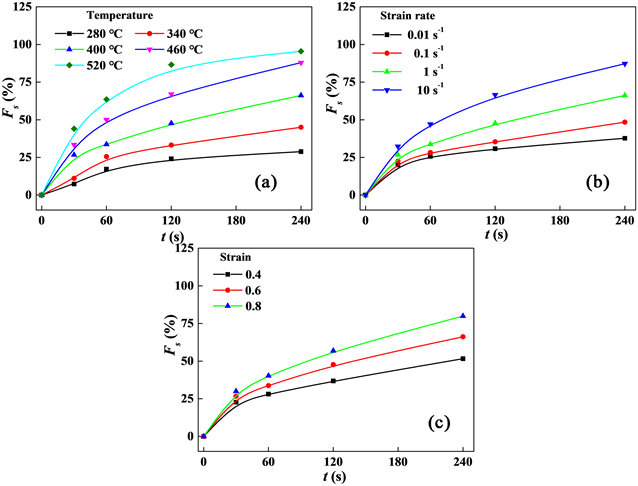
Figure 9. Static softening ratios of Al-4.8Mg alloy under different deformation conditions: (a) $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (b)T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (c)T= 400˚C, $\dot{ε} = 1 s^{- 1}$

图9. Al-4.8Mg合金在不同变形条件下的静态软化率(a) $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(b)T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(c)T= 400˚C， $\dot{ε} = 1 s^{- 1}$

3.3.2. 静态再结晶动力学模型构建

道次间静态再结晶分数X_s可基于力学软化法(即静态软化率F_s)进行研究。由于铝合金热变形过程中易发生动态回复，这将极大削弱静态回复，通常可忽略静态回复对静态软化的影响，并将静态再结晶看成是静态软化的主要原因，且静态再结晶分数与静态软化率之存在式(2)所示的函数关系 [7] 。

$X_{s} = \frac{F_{s} - 0.2}{1 - 0.2} = \frac{F_{s} - 0.2}{0.8}$ (2)

根据式(2)可求出不同变形条件下的静态再结晶分数，如图10所示，随着第一道次变形温度、应变速率、应变量的增大及道次间隔时间的延长，静态再结晶分数逐渐提升，这与第3.2节中微观组织变化特征相匹配。

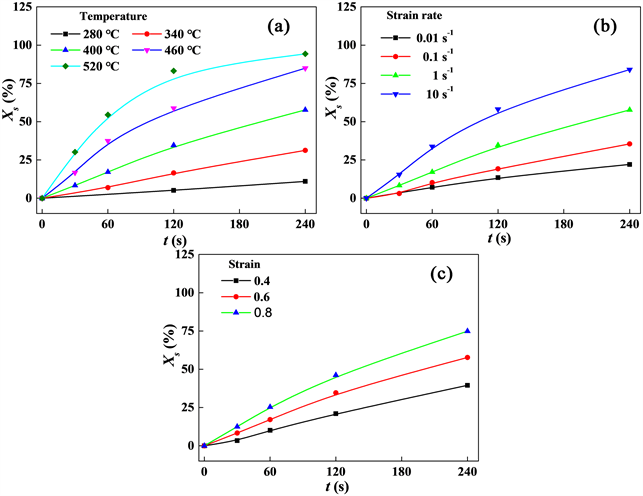
Figure 10. Static recrystallization fractions under different deformation conditions: (a) $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (b)T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (c)T= 400˚C, $\dot{ε} = 1 s^{- 1}$

图10. 不同变形条件下的静态再结晶分数(a) $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(b)T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(c)T= 400˚C， $\dot{ε} = 1 s^{- 1}$

材料热变形后的再结晶行为可用静态再结晶动力学方程描述 [7] ：

$X_{s} = 1 - \exp (- \ln (1 - s) {(\frac{t}{t_{s}})}^{n_{s}})$ (3)

式中：t为道次间隔时间，t_s为静态再结晶分数达到s时所需要的时间，n_s为材料参数。通常按照t_0.5来构建模型，即F_s为70%，由于本文静态软化率F_s在大部分试验条件下不足70% (图9)，因此，取 $t_{s} = t_{0.3}$ 对静态再结晶模型求解。可将式(3)改写成式(4)，其中t_0.3采用式(5)所示的模型进行描述 [7] 。

$X_{s} = 1 - \exp (- 0.357 {(\frac{t}{t_{0.3}})}^{n_{s}})$ (4)

$t_{0.3} = P {\dot{ε}}^{p_{1}} ε^{p_{2}} \exp (\frac{Q_{s}}{R_{c} T})$ (5)

为求解材料参数n_s，对式(4)两边取两次自然对数可得：

$\ln (ln (\frac{1}{1 - X_{s}})) = \ln 0.357 + n_{s} \ln t - \ln t_{0.3}$ (6)

可见n_s为 $\ln {\ln [1 - (1 - X_{s})]} - \ln t$ 的线性斜率。由图10中的数据绘制出 $\ln {\ln [1 - (1 - X_{s})]} - \ln t$ 的关系图并进行线性拟合，可得图11(实心点为试验数据，直线为拟合线)。求出第一道次不同变形温度(图11(a))、应变速率(图11(b))及应变量(图11(c))下各拟合线的斜率，计算其平均值可得：n_s= 1.151。

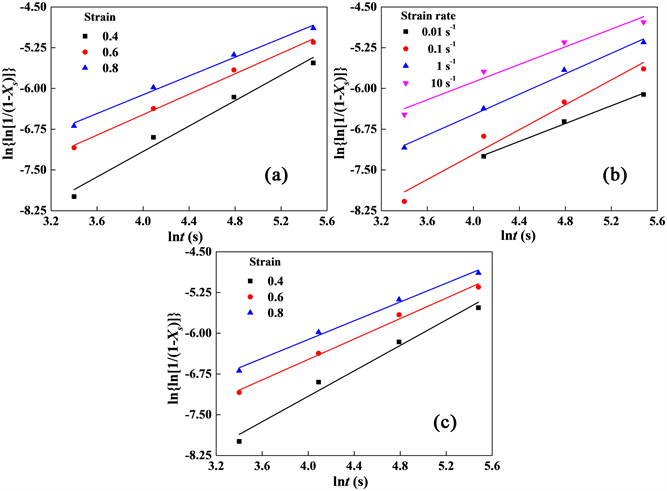
Figure 11. Relations between static recrystallization fractions and deformation conditions: (a) $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (b)T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (c)T= 400˚C, $\dot{ε} = 1 s^{- 1}$

图11. 静态再结晶分数与变形条件的关系(a) $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(b)T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(c)T= 400˚C， $\dot{ε} = 1 s^{- 1}$

为求解P、p₁、p₂和Q_s的值，将式(5)两边取自然对数可得：

$\ln t_{0.3} = \ln P + p_{1} \ln \dot{ε} + p_{2} \ln ε + \frac{Q_{s}}{R_{c} T}$ (7)

由式(7)可知， $Q_{c} / R_{c}$ 、p₁、p₂分别为 $\ln t_{0 .3} - 1/ T$ 、 $\ln t_{0 .3} - \ln \dot{ε}$ 、 $\ln t_{0 .3} - \ln ε$ 的线性斜率。将n_s与图10中的X_s值代入式(4)中，可求得材料在第一道次不同热压缩条件下的t_0.3值，绘制 $\ln t_{0 .3}$ 与1000/T、 $\ln \dot{ε}$ 及 $\ln ε$ 间的关系图并进行线性拟合，可得图12(图中实心点为试验数据，直线为拟合线)。根据图12(a)中 $\ln t_{0 .3} - 1000 / T$ 拟合线的平均斜率可计算出Q_s= 48306 J/mol，求解图12(b)中 $\ln t_{0 .3} - \ln \dot{ε}$ 拟合线斜率的平均值可知p₁= −0.299，由图12(c)中拟合线斜率的平均值可计算出p₂= −1.380。将Q_s、p₁、p₂代入式(5)中，再进行平均值计算，即可求出P= 0.009。

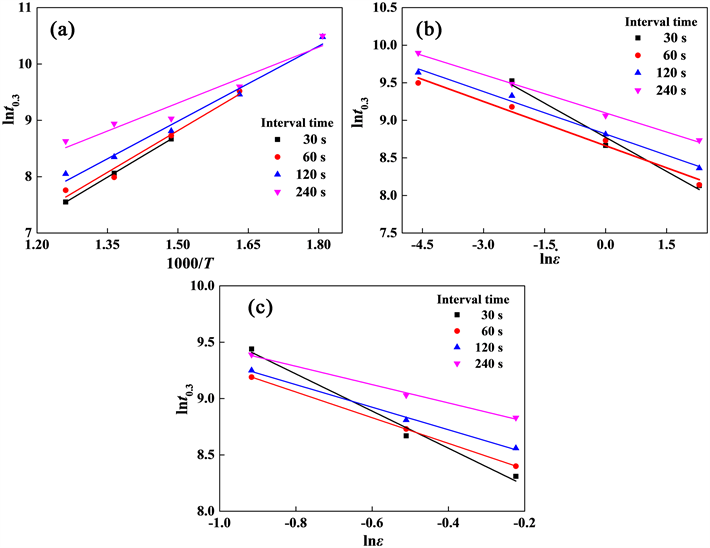
Figure 12. Relations betweent_0.3and deformation parameters: (a) $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (b)T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (c)T= 400˚C, $\dot{ε} = 1 s^{- 1}$

图12.t_0.3与变形参数的关系(a) $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(b)T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(c)T= 400˚C， $\dot{ε} = 1 s^{- 1}$

将n_s、Q_s、p₁、p₂值代入式(4)与(5)中，Al-4.8Mg合金热变形后的静态再结晶动力学模型可表示为：

${\begin{cases} X_{s} = 1 - \exp (- 0.357 {(\frac{t}{t_{0.3}})}^{1.151}) \\ t_{0.3} = 0.009 {\dot{ε}}^{- 0.299} ε^{- 1.38 0} \exp (\frac{48306}{R_{c} T}) \end{cases}$ (8)

3.3.3. 静态再结晶动力学模型的可靠性验证

通过式(8)计算出Al-4.8Mg合金在不同热变形条件及不同道次间隔时间下的静态再结晶分数，并将计算值与试验值进行对比。如图13所示，模型计算值与试验数据吻合良好。通过式(9)计算发现，再结晶分数计算值与试验值的平均相对误差仅为3.8%，说明式(8)所示的静态再结晶动力学模型可对Al-4.8Mg合金热变形后的再结晶分数进行预测。

$A A R E (%) = \frac{1}{N} \sum_{i = 1}^{N} | \frac{X_{s}_{E}^{i} - X_{s}_{C}^{i}}{X_{s}_{C}^{i}} | \times 100 %$ (9)

式中 $X_{s}_{E}^{i}$ 为流变应力试验值， $X_{s}_{C}^{i}$ 为流变应力计算值，N为计算样本数。

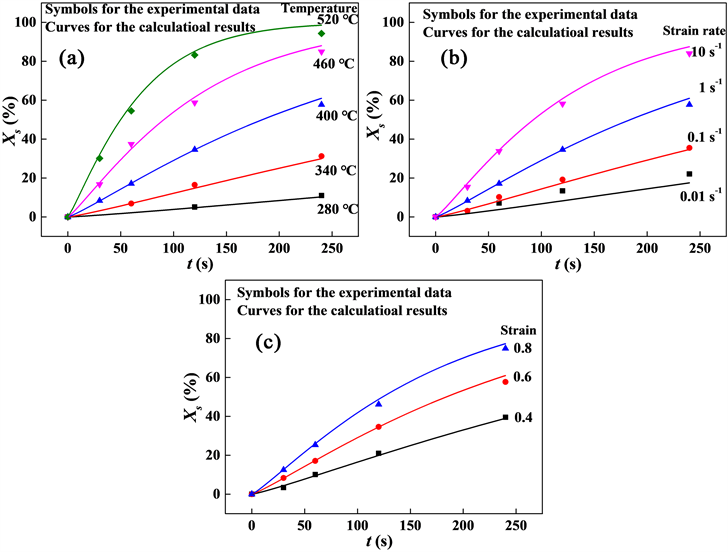
Figure 13. Comparisons between calculational and experimental values of static recrystallization fraction: (a) $\dot{ε} = 1 s^{- 1}$ , $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (b)T= 400˚C, $ε_{1} = 0.6$ , $ε_{2} = 0.3$ ; (c)T= 400˚C, $\dot{ε} = 1 s^{- 1}$

图13. 静态再结晶分数计算值与试验值的对比(a) $\dot{ε} = 1 s^{- 1}$ ， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(b)T= 400˚C， $ε_{1} = 0.6$ ， $ε_{2} = 0.3$ ；(c)T= 400˚C， $\dot{ε} = 1 s^{- 1}$

4. 结论

1) Al-4.8Mg合金双道次热压缩过程中，经过第一道次热变形及道次间停留后，第二道次流变应力相比第一道次呈现出阶梯状下降特征。

2) 提高第一道次的变形温度、应变速率、应变量及延长道次间隔时间，均可提升道次间静态再结晶程度，促进道次间的静态软化。

3) 基于道次间静态软化率构建了Al-4.8Mg合金静态再结晶动力学模型，模型计算值与试验值的平均相对误差仅为3.8%。

基金项目

湖南省科技人才托举工程项目(2022TJ-N19)，湖南省重点研发计划项目(2022GK2041)。

参考文献

[1]	邓运来, 张新明. 铝及铝合金材料进展[J]. 中国有色金属学报, 2019, 29(9): 2115-2141.
[2]	张新明, 邓运来. 新型合金材料——铝合金[M]. 北京: 中国铁道出版社, 2018.
[3]	胥福顺, 陈德斌, 岳有成. 铝及铝合金轧制技术[M]. 北京: 冶金工业出版社, 2019.
[4]	张新明. 铝热连轧原理与技术[M]. 长沙: 中南大学出版社, 2010.
[5]	雷秀川. 5xxx系铝合金再结晶动力学及其形核机制的研究[D]: [博士学位论文]. 重庆: 重庆大学, 2021.
[6]	刘文义. 7085铝合金热加工力学行为及微观组织演变规律研究[D]: [博士学位论文]. 重庆: 重庆大学, 2014.
[7]	肖罡. 6013铝合金多道次变形及本构建模研究[D]: [博士学位论文]. 长沙: 湖南大学, 2016.

为你推荐

友情链接