1. 引言
近年来,随着精准制导武器的广泛使用,打击能力得到了显著改善,从传统的地面攻击转向了更加精准的空中攻击,对于重要的军事基础设施和人防工程构成了极大的挑战。随着政治和其他多方面的挑战,越来越多的爆炸袭击不仅仅是发生在军事基础设施,还有许多民用建筑,比如工厂、汽车站、体育场馆等,都可能成为潜在的危险源。随着近年来计算机技术和硬件的飞速发展,因为爆炸实验的独特性,数值模拟在爆炸载荷下的动态反应已经成为一个越来越受关注的焦点。
多位研究者利用不同的软件和算法,如AUTODYN、ANSYS、LS-DYNA和ABAQUS等,模拟了不同环境和条件下的爆炸效应。研究涵盖了空中爆炸 [1] 、接触式爆炸 [2] 、短距离非接触式爆炸 [3] 以及弹丸冲击 [4] 等多种爆炸类型。此外,陈锐林、王晓磊和申双俊等研究者分别使用了不同的加固材料来研究其对钢筋混凝土板抗爆性能的影响,如陈锐林使用了CFRP [5] ,王晓磊采用了香蕉纤维 [6] ,申双俊则选择了高强钢绞线网片–聚合物砂浆 [7] 。这些研究成功地改善了钢筋混凝土在爆炸冲击下的性能表现。
对于建筑物抗爆性能的研究起初是模型试验。不过因为爆破是一个瞬态事件,所以模型试验的手段可以确定初步与最后的结果,而中间爆破的情况和裂缝的情况是不能直接得到的。由于有限元技术的发达,采用足够多的有限元去研究爆破过程中物质状态的改变,并能够利用计算机手段得到每部分的信息,从而能够更加细致地理解爆破结构。此外大多数关于爆破荷载的研究主要面向远距离爆破。但在远程爆破状态下,爆轰物通过长距离的传播与蔓延,将导致爆破压力均匀分布于建筑构件表面,在近距爆破状态下,爆破带来的高压荷载集中均匀分布于小区域中。因此,在爆炸高度不同的情形下钢筋混凝土板的破裂方式也将会大不相同。
所以,研究对爆破载荷在钢筋混凝土板上较近距离内的动力学反应就变得更为重要,同时也能够通过进一步的基础研究和数值模拟研究,进一步发现其内在的理论实践与创新,从而使得研究能够为改善钢筋混凝土板的耐爆性能,从而对降低或者避免爆破灾害的直接影响,提供理论依据与支持。
2. 爆炸载荷下钢筋混凝土板的数值模拟
由于爆炸实验危险性较高,破坏效果较难预估,实验花费昂贵。故此与WANG等人 [8] 的爆炸实验进行对比验证以证明本文研究方法和参数选取的合理性。
在试验期间,位于钢筋混凝土板上方400 mm距离处的TNT炸药的不同重量(0.2 kg至0.55 kg)产生了爆炸。钢筋混凝土板的试验设置和几何结构如图1所示。
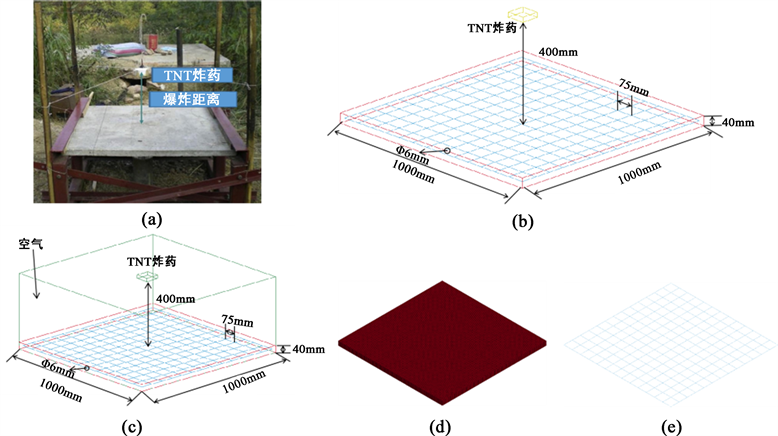
Figure 1. Experimental setup and geometric modeling diagram, (a) experimental setup, (b) geometric modeling, (c) finite element model, (d) concrete model, (e) steel bar model
图1. 试验装置与几何建模图,(a)试验装置,(b)几何建模,(c)有限元模型,(d)混凝土模型,(e)钢筋模型
该试验由尺寸为1000 mm × 1000 mm × 40 mm混凝土板,一层直径为6 mm,间距为75 mm的正交钢筋,以及位于钢筋混凝土板正上方400 mm处的TNT炸药组成。
为了验证数值模型的可靠性和准确性,模拟了钢筋混凝土板在爆炸荷载下的动态响应。
3. 材料模型
3.1. 混凝土材料模型
在LS-DYNA中,软件对单位并没有进行严格规定,这需要用户自行保证单位一致,所以除非特殊说明单位为kg-mm-ms。
混凝土的单元属性使用实体单元SOLID164对混凝土进行建模,元素方程式选择1号方程即定应力实心元件,该实体单元是由8个节点组成的六面体单元,而且该单元能够退化为6节点的三棱柱形状,还能退化成4节点的三棱锥形状,这使得在单元发生大变形的时候,单元网格可以自动适应当前的结构,从而避免过大变形时候的单元失效,进而影响最终结果;选择该单元的积分计算为单点积分算法;单元的计算方法为拉格朗日(Lagrange)计算方法;并且该单元在施加荷载的时候,压力只能施加在单元的某一个面上。
当下在有限元模拟领域,混凝土的本构模型一般有HJC模型 [9] 、RHT模型 [10] 、CSCM模型 [11] 、K & C模型 [12] 。因此,要想准确地描述混凝土材料的基本力学特性,需要对上述模型的参数作出系统地调整。通过在以往的混凝土爆炸冲击的数值模拟研究中,运用较多的是The Karagozian & Case Concrete Model-Release I II即K & C本构模型 [13] ,K & C模型是一个三不变模型,使用三个剪切破坏面,包括损伤和应变率效应,可以纳入实验数据进行考量,也可以设置动态增量因子(DIF),该因子可以表明当施加力的速度加快的时候材料的表现状况是否发生突变,并且该模型的压力-体积应变反应需要方程式来定义,其起源基于伪张量模型,即LS-DYNA的第16号模型,该模型常用于分析埋地钢筋混凝土结构在脉冲荷载作用下的受力情况。并且K & C模型还需要定义压力–体积方程式,这由*EOS_TABULATED_COMPACTION来定义的,该方程式很好的考虑到了混凝土类材料的应变率效应、应变硬化软化现象等,这些能够准确地描述混凝土类材料在大变形、高应变率,特别是爆炸作用的大变形中表现尤为优秀。其中K & C模型,定义损伤方程为:
(1)
在式中:
为损伤的转折;
是材料内部的损伤变量,
表达式为:
(2)
(3)
式中:p为静水压力;b1和b2为受压和受拉的损伤控制因子;ft为材料的抗拉强度;
为材料的等效塑性应变,
为材料的等效塑性应变增量;
为材料的塑性应变张量 [14] 。
本文混凝土材料采用的K & C模型主要参数如表1所示。表1中A0为最大剪切破坏面参数,RSIZE和UCF分别为长度单位和应力单位的换算系数。

Table 1. Main parameters of concrete material model
表1. 混凝土材料模型主要参数
为了更好地模拟混凝土的损伤情况,本文引入了LS-DYNA侵蚀算法。引入侵蚀算法可以使得模拟过程更加平滑,且侵蚀算法已经广泛应用于爆炸载荷对于混凝土破坏的模拟 [15] 。虽然LS-DYNA中的许多本构模型不带有破坏或侵蚀的算法,但是LS-DYNA提供了一种在这些模型中可以实现单元失败的方法即*MAT_ADD_EROSION,这样用户可以通过设定其MXEPS参数来规定当前应用该属性的材料在失效时的最大应变。但是,值得注意的是,如果用户设定的标准过于低的时候,就会导致材料的质量与能量不在守恒,这是由于该侵蚀过程是不可逆的,这也会导致模拟结果不再可靠。设定了其MXEPS为0.1,即表明该材料在最大应变程度达到0.1的时候,发生破坏,并在发生破坏以后删除该单元以加快计算速度。
3.2. 钢筋材料模型
钢筋的单元属性使用梁单元BEAM161对混凝土钢筋进行建模,元素方程式选择1号方程即定应力实心元件,该单元有三个节点组成,其中K节点用来定义截面的初始方向,单元的截面类型可以为矩形或圆形等截面,单元的截面必须结合实常数来确定截面的大小,单元的压力荷载必须要施加在单元的某一面上,不能施加体荷载,单元的截面积分规则为标准积分,单元的计算效率和计算的稳定性较好,且单元包含有限的横向切应变;
钢筋选用*MAT_PLASTIC_KINEMATIC这一塑形随动材料模型。该模型不仅适用于速率效应的各向同性和运动硬化塑性模型的考量,还可以通过调整硬化参数
来选择各向同性硬化(
)或者随动硬化(
)。应变率效应的影响则是通过Cowper-Symonds模型来考虑,用与应变率有关的因数表示屈服应力,强化后的屈服应力的公式可以表示为 [14] :
(4)
(5)
在公式(4)和(5)中:
为因应变率效应强化后的屈服应力,
为静载作用下材料的屈服应力,
为应变率,C和P为Cowper-Symonds模型的应变率参数,
为硬化参数,
为塑形硬化模量,
为有效塑形应变,
为切线模量,E为弹性模量。
选用的钢筋参数如表2所示。

Table 2. Main parameters of steel bar material model
表2. 钢筋材料模型主要参数
同样的为了更好地模拟钢筋的损伤情况,钢筋模型也引入了侵蚀算法。在*MAT_ADD_EROSION中将MXEPS参数设定为0.2,这要比混凝土的最大应变大,这是因为钢筋的塑性要比混凝土更强。
3.3. 空气与炸药的材料模型
本文空气与炸药部分的单元属性均为实体单元SOLID164,但元素方程式选择11号即单点ALE多材料元素,ALE算法结合Lagrange算法和Euler算法的优点,虽然它也是把网格和物质结构相互独立开来的,但是网格不再固定在空间中,而是能够根据定义的参数在求解的过程中追踪结构物质点的运动,但是又不至于使网格发生过大的变形导致计算精度的下降或者不收敛。
空气部分的材料通过选择*MAT_NULL来设定,在固体的情况下,这种材料允许考虑状态方程而不计算偏应力,还可以定义粘度。此外,拉伸和压缩中的侵蚀也是可以的 [14] 。其主要参数如表3所示:

Table 3. Main parameters of the air material model
表3. 空气材料模型主要参数
由于定义的空气单元属性为solid,则材料必须定义截止压力,这是一个负值的张力。并且膨胀应力或压力是负的,这会将截止压力极限设置为一个非常小的负数,允许材料空化,一旦材料中的压力低于这个负值,材料就不再能够抵抗这种膨胀。
此外,还需要通过*EOS_LINEAR_POLYNOMIAL定义空气的控制方程,其压强由方程6定义 [14] :
(6)
线性多项式状态方程可用伽马定律状态方程来模拟气体。这可以通过设置:
并且
,其中
,那么这个理想气体的压强就是:
(7)
通过定义C4、C5、E0和V0参数来初始化空气材料的热力学状态,其中E0为单位参考体积的初始内能,V0为初始相对体积。其主要参数如表4所示:

Table 4. Main parameters of the air material control model
表4.空气材料控制模型的主要参数
炸药部分的材料通过设定*MAT_HIGH_EXPLOSIVE_BURN来确定的,它可以模拟烈性炸药的起爆过程,其主要参数如表5所示:

Table 5. Main parameters of explosive material model
表5.炸药材料模型主要参数
此外,还必须定义炸药的状态方程,本文采用*EOS_JWL,JWL状态方程,用于定义烈性炸药的爆轰产物,JWL状态方程的压力定义为:
(8)
该状态方程的主要参数为A、B、R1、R2与
分别是373.77 GPa、3.7471 GPa、4.15、0.9和0.35。
3.4. 沙漏控制
为防止全积分单元引起的构件刚度较大、计算时间较长等问题,混凝土材料单元属性采用的是单点缩减的积分(即SOLID164),而采取这种积分的单元容易出现沙漏现象。
沙漏现象表现为仅仅需要很小的扰动就可以在理论上使得单元持续变形却不消耗能力,这违背了物质能量守恒的定理,而且沙漏会导致单元网格失去刚度,变形成为锯齿形网格。
所以欲使沙漏这种现象得以抵制,可以通过设定*HOURGLASS人为的消耗一定的能量,当然,如果人为设定的能量过多,会导致模型与实际的变形有很大的差别。
*HOURGLASS的IHQ参数代表hourglass节点的分布控制因子。该参数的值越小,hourglass节点的分布越均匀,材料的变形也越稳定,但同时也会增加计算时间。相反,该参数的值越大,hourglass节点的分布越不均匀,材料的变形也越不稳定,但计算时间会相应减少。因为炸药爆炸之后产生的冲击波在空气这种比较均匀的介质中,爆轰产物与空气的变形都是稳定的,所以这里设置ALE部分part的IHQ为1,又因为钢筋混凝土板的不是均匀的介质,特别是混凝土与钢筋接触部分的介质突变,计算时间非常长,所以设置language部分part的IHQ为3,这样可以减少计算时间。
3.5. 数值模型
本文建立了包括TNT炸药、空气、钢筋以及混凝土板在内的三维实体模型来模拟爆炸的试验过程。其中钢筋混凝土结构中混凝土与钢筋接触算法采用的是*CONSTRAINED_LAGRANGE_IN_SOLID,这种算法可以将炸药爆炸时混凝土受到的力准确的传递给钢筋。此建模方法可以更加真实地反映钢筋混凝土结构的力学性能。
在模拟中,混凝土板和钢筋采用拉格朗日(language)计算方法,其中坐标随材料移动。炸药和空气采用拉格朗日-欧拉(ALE)计算方法来划分网格。流固耦合算法为流固耦合建模提供了合适的耦合机理,将空气收到的力均匀、准确的传递给混凝土。空气的边界条件设为非反射边界,这样既可以减少计算时间,也能够忽略掉反射回的力以防止干扰最终结果。
3.6. 试验设置
表6给出了试验的详细信息,其中包括前4组汪维 [8] 试验的数值模拟验证,以及后面8组钢筋混凝土板的板厚对于抗爆性能的研究试验。
根据实际试验装置以及试验分组,建立的有限元三维几何模型如图1所示。
4. 数值模拟结果与试验结果比较
图2显示了试验1到试验4的数值模拟中获得的钢筋混凝土板等效塑性应变的比较。
其中试验1 (0.2 kgTNT,400 mm爆炸距离),如图2(a)和图2(b)所示,迎爆面没有明显的损伤,而背爆面中心有略微掉落,图2(d)的中心区域的绿色部分为少量混凝土剥落而露出内部的混凝土,这恰如图2(c)所示,且裂缝很少如图2(c)和图2(d)。可以比较明显的看出混凝土板内部钢筋对于板的保护。
在试验2 (0.31 kg TNT,400 mm爆炸距离)里,如图2(e)和图3(f)所示,在板坯中心有一个小区域发生了压碎损坏,其上表面被一些径向和周向裂纹包围,而模拟结果中心区域,有少量剥落。如图2(g)和图2(h)所示,混凝土板的后部塌陷,并形成拉伸剥落坑,而模拟结果中心的剥落区域更大。从实验结果中可以清楚地观察到一些广泛的裂纹。
在试验3 (0.46 kg TNT,400 mm爆炸距离)里,图2(i)显示了更多的周向裂纹,这是由于自由表面反射的拉伸波产生的强大的压力导致混凝土材料压缩形成,在上表面的中心形成一个小的损坏区域,图2(j)也显示了这一点。如图2(k)所示,底部表面中心有一个方形剥落损伤区域,且四向的裂纹变得更多。图2(l)中的数值结果中等效塑性应变也由图2(h)变为由中心向四周辐射的形状。

Figure 2. Comparison of Numerical Results and Experimental Results for the Damage Contour of Reinforced Concrete Slabs: (a) Experimental Results on the Facing Surface of Experiment 1, (b) Numerical Results on the Facing Surface of Experiment 1, (c) Experimental Results on the Facing Surface of Experiment 1, and (d) Numerical Results on the Facing Surface of Experiment 1; (e) The experimental results of the front detonation surface in Experiment 2, (f) the numerical results of the front detonation surface in Experiment 2, (g) the experimental results of the back detonation surface in Experiment 2, and (h) the numerical results of the back detonation surface in Experiment 2; (i) The experimental results of the front detonation surface in Experiment 3 (j), the numerical results of the front detonation surface in Experiment 3 (k), the experimental results of the back detonation surface in Experiment 3 (l), and the numerical results of the back detonation surface in Experiment 3; (m) Experimental Results of Experiment 4 on the Face of Explosion (n) Numerical Results of Experiment 4 on the Face of Explosion (o) Experimental Results of Experiment 4 on the Face of Explosion (p) Numerical Results of Experiment 4 on the Face of Explosion
图2. 钢筋混凝土板损伤轮廓数值结果和实验结果的比较:(a)试验1迎爆面的实验结果,(b)试验1迎爆面的数值结果,(c)试验1背爆面的实验结果,(d)试验1背爆面的数值结果,(e)试验2迎爆面的实验结果,(f)试验2迎爆面的数值结果,(g)试验2背爆面的实验结果,(h)试验2背爆面的数值结果,(i)试验3迎爆面的实验结果,(j)试验3迎爆面的数值结果,(k)试验3背爆面的实验结果,(l)试验3背爆面的数值结果,(m)试验4迎爆面的实验结果,(n)试验4迎爆面的数值结果,(o)试验4背爆面的实验结果,(p)试验4背爆面的数值结果
在试验4 (0.55kg TNT,400 mm爆炸距离),图2(m)中钢筋混凝土板弯曲并出现轴向破坏,在中心形成一个穿孔,板上部的混凝土主要由于高压缩爆轰产物而失效,但后背破坏的范围更大。当塑性应力波到达板的后部时,会形成反射的拉伸波,导致底部混凝土坍塌。其中图2(p)中心的绿色部分为底层剥落以后,露出的内部混凝土与钢筋,数值模拟的损伤结果与实验现象一致。
由于炸药会造成不同的应力和失效区域,在爆炸以后的气体膨胀的过程中,爆轰产物的流动速度远大于初始空气声速,这使得产生了一个介质与压强均会突变的区域,在一定的时间下,会因过度膨胀而出现反向作用力且压力范围更大的负压区。故此爆炸会造成不同的应力和失效区域使得钢筋混凝土板在上表面和下表面之间发生穿孔损伤或不同损伤。以试验4为例,钢筋混凝土板的破坏过程如图3所示。
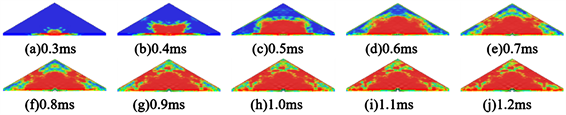
Figure 3. The peeling damage process of reinforced concrete slabs at different times
图3. 钢筋混凝土板在不同时刻的剥落损伤过程
钢筋混凝土结构的建模与仿真对工程具有重要意义。从图3中可以看出,板的倒塌导致钢筋变形。以试验4为例,图4显示了爆炸荷载下钢筋的压力等值线。它显示了压缩应力和拉伸应力的分布,以及钢的变形过程。变形主要发生在板的中心部分,这部分钢筋屈服,但没有断裂。另一方面,这表明钢筋的存在在一定程度上减少了混凝土的结构损伤。
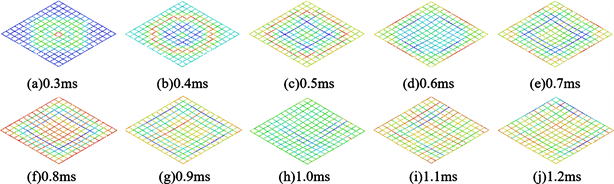
Figure 4. The evolution process of the axial force combination of steel bars
图4. 钢筋的轴向力合力演变过程
尽管模拟结果和实验结果之间存在一些偏差,但总体来说一致性较好,这表明了建模方法以及参数选择的合理性。
5. 不同炸药量、不同厚度的钢筋混凝土板的裂缝损伤模拟
5.1. 混凝土板配置
在以下研究中,对不同爆炸条件下钢筋混凝土板的损伤进行了数值模拟研究。其中钢筋混凝土板的长度和宽度均为1000 mm,三种不同深度的板分别为40 mm、80 mm和120 mm,TNT炸药的装药量分别为0.2 kg、0.31 kg、0.46 kg和0.55 kg,炸药到板的距离均设置为400 mm,并以Z轴位移来量化板的损伤程度。模拟中使用的材料参数与第2节中使用的参数相同。
5.2. 模拟结果与讨论
5.2.1. 等炸药质量,不等板厚的对比
以同等炸药量0.2 kg为例,图5显示了试验1 (0.2 kg TNT,40 mm板厚)、试验5 (0.2 kg TNT,80 mm板厚)和试验9 (0.2 kgTNT,120 mm板厚)在数值模拟中获得的钢筋混凝土板等效塑性应变的迎爆面与背爆面的比较。如图5所示,三种厚度的混凝土板的迎爆面均没有明显的损伤,而背爆面因为图5(d)背部剥落,致使冲击波得到释放,没有产生过多的裂纹,而除了图5(a)的中心有一定的剥落漏出内部混凝土之外,图5(e)与图5(f)的板均有剥落的趋势,而120 mm板厚的较80 mm板厚的裂纹明显减少,故此随着板的厚度的增加,可以明显看出爆炸对板损伤程度的降低。

Figure 5. (a) Test 1 explosion facing surface, (b) Test 5 explosion facing surface, (c) Test 9 explosion facing surface; (d) Test 1 back burst surface, (e) Test 5 back burst surface, (f) Test 9 back burst surface
图5. (a)试验1迎爆面,(b)试验5迎爆面,(c)试验9迎爆面,(d)试验1背爆面,(e)试验5背爆面,(f)试验9背爆面
图6显示的是爆炸载荷为0.2 kg的,不同板厚度的,钢筋混凝土板中心受爆区域在Z轴上的位移曲线。可以看出,在板厚仅为40 mm时,板中心受爆区域位移最大,且变化速度也最快,而板厚为80 mm时,不仅板中心爆炸区域的位移明显减少,并且变化速度显著变缓,而板厚为120 mm时,比80 mm效果更好,但变化速度较80 mm相差不多。
5.2.2. 不等炸药质量,等板厚的对比
以同等板厚80 mm为例,图7显示了试验5 (0.2 kg TNT,80 mm板厚)、试验6 (0.31 kg TNT,80 mm板厚)、试验7 (0.46 kg TNT,80 mm板厚)和试验8 (0.55 kg TNT,80 mm板厚)在数值模拟中获得的钢筋混凝土板等效塑性应变的迎爆面与背爆面的比较。如图7所示,对于四种不同质量的炸药在混凝土板的迎爆面均没有明显的损伤,如图7(a)所示,当炸药质量为0.2 kg时并没有产生大面积的等效塑性应变,而如图7(d)所示,当炸药质量到0.55 kg时,迎爆面并不比0.46 kg时产生的等效塑性应变更多,且从背爆面来看如图7(g)和图7(h)所示,也并没有产生过多的裂纹。故此随着炸药质量的增加,板的损失程度在加剧,但当炸药质量到达0.46 kg以后到0.55 kg时,对于相同板厚的损伤,没有发生太大的变化。

Figure 6. Displacement Curve of the Explosion Center of 0.2 kg Explosives with Different Plate thicknesses
图6. 不同板厚0.2 kg炸药的板受爆中心位移曲线
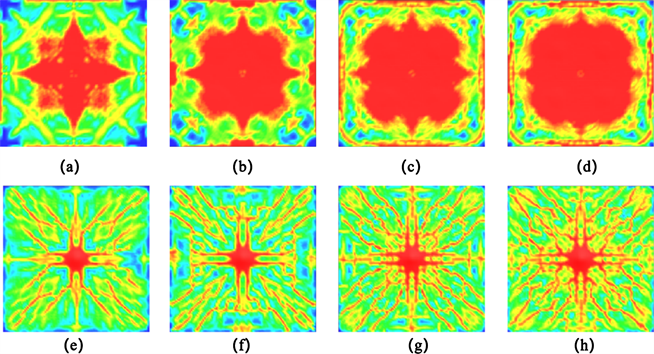
Figure 7. Comparison of the front and back explosive surfaces with a plate thickness of 80 mm (a) Test 5 front explosive surface (b) Test 6 front explosive surface (c) Test 7 front explosive surface (d) Test 8 front explosive surface (e) Test 5 back explosive surface (f) Test 6 back explosive surface (g) Test 7 back explosive surface (h) Test 8 back explosive surface
图7. 板厚为80 mm的迎爆面及背爆面的比较,(a)试验5迎爆面,(b)试验6迎爆面,(c)试验7迎爆面,(d)试验8迎爆面,(e)试验5背爆面,(f)试验6背爆面,(g)试验7背爆面,(h)试验8背爆面
5.2.3. 不等炸药质量,不等板厚的对比
图8是通过等高线图表示的炸药量、板厚与Z轴位移的关系,图中X轴为炸药量的递增,Y轴为板厚度的递增,而板的Z轴位移是通过颜色从蓝色到红色渐变来表示,即图标从上往下表示Z轴位移的大小也就是对于板损伤程度的映射,可以看出当板厚越薄,炸药量越多的时候,板的损伤程度越大。值得注意的是图8并不是呈对角对称的,当板厚度达到80 mm时,一定剂量的炸药量增加不会造成更严重的板损伤,从120 mm板厚到80 mm的板厚中板损伤程度的变化率较小,而从80 mm的板厚降低到40 mm板厚的过程中,板损伤程度的变化率较大,并且在80 mm到40 mm的板厚区间里,即使是少量炸药剂量的变化也会造成更大的损伤。从材料力学的角度来说钢筋混凝土板的抗爆性能主要取决于其厚度和材料本身的强度。随着板厚的增加,板的强度和刚度也会增加,因此对爆炸的抵抗能力也会增强。当板厚达到一定的值时,板的强度和刚度已经达到临界值,再增加板厚对抵抗爆炸的能力提升不明显。而从爆炸冲击的角度来说爆炸产生的冲击波在传播过程中,会逐渐减弱。当钢筋混凝土板的厚度足够大时,冲击波可能无法完全穿透板,因此再增加少量的炸药,也无法造成更严重的板损伤。但是,当板厚减小到一定程度(例如从80 mm降低到40 mm),冲击波可以更容易地穿透板,因此板的损伤程度会显著增加。
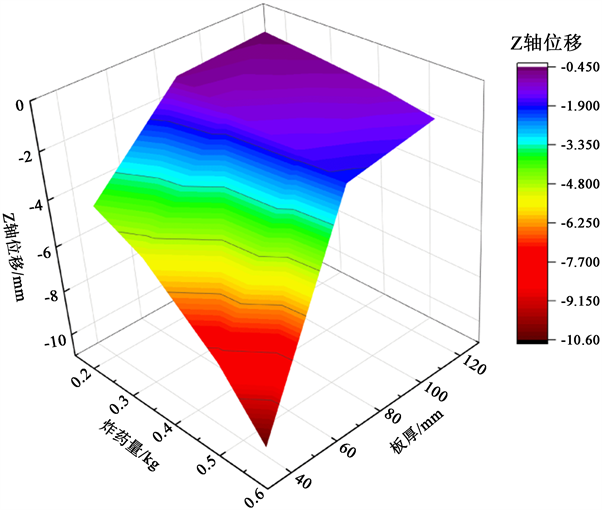
Figure 8. Effect of different explosive amounts and plate thicknesses on Z-axis displacement
图8. 不同炸药量与不同板厚对Z轴位移的影响
6. 结论
通过上述研究得出以下结论:
1) 通过与已有的爆炸实验进行对比,证明了本文模拟研究方法与参数设定的可行性并为下文的试验保证计算模型和实际爆炸过程一致性。
2) 在所有的实验中都体现了在同等条件下,板的背爆面反而损伤更大,建议在实际应用时加强背爆面的有效防护。
3) 在所有的实验中,发现板的抗爆性能的增加并不是与板的厚度呈线性相关的。其中在板厚小于80 mm时,钢筋混凝土板的厚度增加,板的抗爆性能增强速度平缓,少量炸药质量的增加也会对板的抗爆性能影响较大。而当板厚大于80 mm到120 mm的时候,板的抗爆性能增强速度大大加快,少量炸药质量的增加并不会对板造成更多的损伤。
致谢
感谢老师,感谢自己。
基金项目
山东省人民防空科技创新项目2020RF009。