1. 引言
在遥感影像融合中,由于成像传感器的物理限制,很多遥感卫星无法直接得到高分辨率多光谱图像 [1] 。为了得到更有信息量的多光谱图像,提高图像的解译精度及利用率,学者们融合全色图像和多光谱图像,将全色图像中的空间信息和多光谱图像中的光谱信息相结合,获得高空间分辨的多光谱图像。全色与多光谱遥感图像融合在特征提取、目标检测和分类等方面发挥着重要的作用。因此,怎样合理有效的进行全色和多光谱图像融合也成为了遥感图像融合研究的重点和难题。
当前遥感影像融合方法可分为以下几类:基于传统方法的融合:常用的算法包括算术平均法 [2] 、加权平均法 [3] 、PCA法 [4] 、小波变换 [5] 、多分辨率分析 [6] 、高斯金字塔 [7] 、非下采样剪切波变换(Non-Subsampled Shearlet Transform, NSST) [8] 等。熊璋玺等 [9] 提出了一种基于非下采样剪切波变换,将区域清晰度加权与导向滤波有机地结合的遥感图像融合算法,在提升遥感图像空间分辨率的同时也非常有效的保留了光谱信息。杨晟炜等 [10] 将IHS和NSST相结合,将RGB图像变换到相关性最小的IHS颜色空间,得到了光谱信息和空间细节更好的图像。Weiguo Wan [11] 提出了一种基于非下采样剪切波变换,将PCA和HIS相结合的图像融合算法,提高了融合图像的空间分辨率,增强了空间细节,减少了光谱失真现象。孙岩等 [12] 将PCA与NSCT使用不同的规则进行结合,再进行PCA逆变换和NSCT逆变换得到融合图像,提高了融合图像的空间质量。符娇等 [13] 将PCA和NSST相结合,利用加权最小二乘滤波获得多尺度空间的细节信息,提高了融合图像的细节信息,同时有效避免了光谱失真。苗启广等 [14] 首次提出一种利用非负矩阵分解得到的融合图像的算法,该算法的适用性较高,并且能够更好地保留图像中的边缘信息。李红等 [15] 提出了一种在低分辨字典下获得光谱系数矩阵,使用稀疏非负矩阵分解(SNMF)的融合方法,该算法稳定高,且融合图像具有更好的光谱信息和空间信息。
基于深度学习的融合:该方法通过卷积神经网络(CNN)等深度学习技术,从数据中自动学习特征,在保留图像细节信息的同时实现对遥感影像的融合和增强。常用的算法包括U-Net [16] 、YOLOv5s [17] 等。陈世权等 [17] 提出了一种YOLOv5s和图像融合相结合的行人检测方法,引入SENet通道优化网络结构,既保持了原算法的高实时性,也提升了融合图像的效果。蔺素珍等 [18] 提出了一种基于深度堆叠卷积神经网络的融合方法,利用高斯拉普拉斯滤波器和高斯滤波器作为首层网络的初始卷积核,利用He K方法初始化其余层卷积核,得到的融合图像具有更高的对比度和清晰度。陈国洋等 [19] 提出了一种无监督的端到端的深度融合算法,利用方差加权的方式计算损失函数,将注意力机制引入到模型,提升了融合结果。
传统方法和深度学习相结合的融合方法,例如NSST-PCNN算法、NSST-HIS算法。沈瑜等 [20] 把NSST与脉冲耦合神经网络相融合,构建显著性矩阵进行自适应加权融合,提高了融合图像的对比度,更好的保留原始图像的细节信息。Kong WW等 [21] 使用NSST对源图像进行分解与重构,另外使用一种神经元网络模型负责同尺度和方向上子图像的融合,融合结果在视觉效果和客观评价上都有显著提高。杨艳春等 [22] 提出NSST和IFCNN的图像融合方法,很好地保留图像的细节信息,减少伪影和噪声,具有良好的视觉效果。本文将NFM与NSST相结合,提出了一种有效融合全色图像和多光谱图像的算法。
本文贡献:
1) 与小波算法、区域能量算法、HIS算法、NSST-PCNN算法和NSST-PCA算法五种融合方法进行对比实验,本文采用了5种客观评价方法进行数据分析,验证了本文提出的算法的有效性及优越性。
2) 本文使用NSST可以多个方向分解特性将全色图像和多光谱影像分解为高频和低频子带图像,低频子带图像通过非负矩阵分解融合得到低频图像,高频子带图像经过参数自适应脉冲耦合神经网络(PA-PCNN)融合得到高频图像,得到的低、高频图像再融合为分辨率高的遥感图像,有效的保留了遥感图像的光谱信息和空间细节。
3) 非负矩阵分解有效地减少了图像融合的空间和光谱失真现象,并挖掘了不同光谱波段之间的稀疏性。本文提出了一种将NFM与NSST相结合的遥感图像融合算法,有效地保持原始图像的光谱信息和空间信息。
2. 相关工作介绍
2.1. 非下采样剪切波变换
NSST是一种多尺度分析方法,它的主要目的是在保持图像结构信息的同时避免伪吉布斯现象。从数学角度来看,NSST可以被认为是剪切波变换(Shearlet Transform)的扩展版本,其基本思想是通过可分离的滤波器组对图像进行多尺度分解。
具体而言,NSST分为两个阶段:多尺度分解和方向定位。其中,多尺度分解是通过对图像进行可分解的非采样金字塔滤波器组NSLP分解来实现的。这种过程旨在保留图像中的结构信息,并且能够抑制伪吉布斯现象。NSLP采用非线性滤波器组对信号进行下采样,并利用逼近系数重建图像。此外,NSST还使用了可分离的剪切波滤波器来实现方向敏感的处理。剪切波滤波器能够在不同方向上捕捉图像中的局部结构,并将其表示为脊线和边缘。在方向定位阶段,NSST使用了剪切波滤波器进行处理,以实现对边缘和曲线的高效率处理。剪切波滤波器是一种多尺度、多方向的变换,可以捕捉图像中的各个方向上的结构信息,并对图像信号进行精确的分析。前者将图像分解为多个尺度,而后者则在图像上进行方向定位。NSST的多尺度和多方向分解过程如下图1所示。
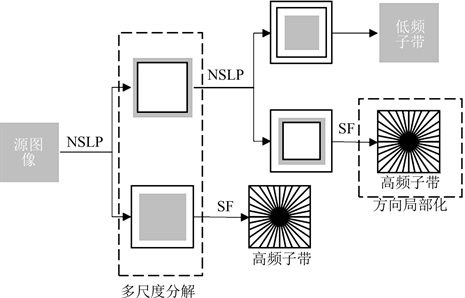
Figure 1. Multi-scale and multi-direction decomposition process of NSST
图1. NSST的多尺度和多方向分解过程
NSLP指非下采样拉普拉斯金字塔滤波器组,用于多尺度分解,SF指剪切波滤波器,用于方向定位。NSST不仅具有多尺度特性,而且具有较强的平移不变性和方向敏感性。与其他方法相比,NSST的剪切波滤波器具有更好的局部化性质,因此能够更准确地表示图像中的边缘等细节信息。总体而言,NSST是一种具有很高应用价值的图像处理方法,已经在许多领域中得到广泛应用。该方法通过多尺度分解和方向敏感的处理方式,能够更好地保留和表达图像的结构信息和细节信息,从而获得更高质量的图像处理结果。
2.2. 非负矩阵分解
非负矩阵分解是一种基于矩阵分析的方法,可以有效地提取不同图像等数据的主要特征信息。该方法将原始矩阵分解为两个非负矩阵——基矩阵W和系数矩阵H,并且它们的乘积能近似等于原始矩阵V。在分解过程中,假设矩阵V的每个元素均为非负数。如果存在噪音或误差,我们可以使用基矩阵W中每一列的线性加权和来表示对应的列数据,以达到降噪效果。由于W和H矩阵受到非负约束条件,因此能够学习到V中数据的局部属性,从而体现了局部代表整体的思想,W和H的求解可以转化为最小化的目标函数,其中基于欧氏距离的目标函数如下:
E(V|WH)=|V−WH|2F=M∑i=1N∑j=1(Vij−(WH)ij)2 。
2.3. 参数自适应脉冲耦合神经网络
脉冲耦合神经网络(PCNN)模型是一种常用于图像处理的算法,但它包含了多个需要确定的参数,而这些参数与最终的效果之间的关系并不明确。为了提高分类准确性和鲁棒性能,人们提出了自适应脉冲耦合神经网络(PA-PCNN)模型。
在PA-PCNN模型中,将每个像素作为一个神经元,并以该像素的灰度值作为其外部刺激。神经元的内部活动项由耦合连接子系统和反馈输入子系统的信号相乘调制得到U,然后与阈值θ进行比较。若U > θ,则神经元被触发点火,Y = 1;否则,Y = 0。整个过程将不断迭代进行,直到满足某些条件为止。经过多轮迭代后,所有神经元点火的次数构成了一个点火映射图,图2可作为PA-PCNN模型的输出结果。PA-PCNN模型不仅保留了PCNN模型的重要特性,同时还具有更好的分类效果和鲁棒性能。
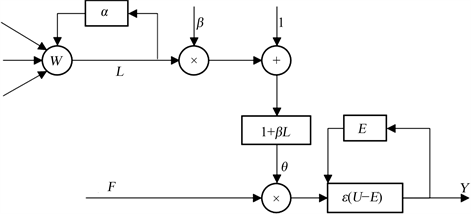
Figure 2. Output process of PA-PCNN model
图2. PA-PCNN模型的输出过程
3. 所提算法
本论文提出了一种新的融合算法,该算法充分利用了NSST的多尺度和NMF的效率优势,以获得具有更高空间和光谱继承性的图像。该算法需要将红外图像和可见光图像输入到算法程序中。该算法包括非下采样剪切小波变换算法、非负矩阵分解算法和参数自适应脉冲耦合神经网络(PA-PCNN)算法。NSST将红外图像和可见光图像分解为高频和低频子带图像。低频子带图像通过非负矩阵分解进行融合,以获得低频图像。高频子带图像通过参数自适应脉冲耦合神经网络进行融合,以获得高频图像。然后将获得的低频和高频图像融合成高分辨率遥感图像。
本过程使用的算法处理过程如图3所示,详细理解如下:
1) 使用NSST算法分解可见光图像和红外图像,以获得低频子带图像VA和VB以及高频子带图像
Hi,lA 、
Hi,lB ,j和l分别是分解层数和第j层中的通道数;
2) 获得的高频子带图像
Hi,lA 和
Hi,lB 使用参数自适应脉冲耦合神经网络(PA-PCNN)进行融合,以捕获高频图像的边缘和细节,从而获得高频融合图像;
3) 使用非负矩阵分解算法对低频子带图像VA和VB进行融合,以获得低频融合图像;
4) 对高频融合图像和低频融合图像执行NSST逆变换,以获得融合图像。
3.1. 低频融合部分
NMF是一种在图像处理和计算机视觉领域中广泛使用的方法。它可以将一个非负矩阵分解为两个或多个较小的非负矩阵,从而更好地表示原始数据。在图像融合中,NMF可以用于将两种或更多种图像结合成一个新的图像。
该方法的基本原理是将原始图像表示为两个矩阵的乘积A = WH。
其中矩阵W和H是非负的。矩阵W包括原始图像的空间信息,矩阵H则包括原始图像的特征信息。
图像融合中,我们可以将两个不同的图像分别分解成两个非负矩阵,并利用它们的矩阵W和矩阵H来合成一个新的图像。合成的图像可以通过调整矩阵W和H中的值来控制原始图像的融合程度。因为两个图像的像素值都是非负的,所以在这种方法中,非负性约束是非常重要。当我们使用使用非负矩阵分解这种方法进行图像融合,就可以保证合成的图像也保持非负性。
总体来说,非负矩阵分解在图像融合中的原理是通过将原始图像表示为两个非负的矩阵,然后使用这些矩阵来合成一个新的图像。这种方法可以很好地保持原始图像的特征,并提供更大的控制来调整融合程度。
3.2. 高频融合部分
高频图像使用参数自适应脉冲耦合神经网络(Parameter Adaptation Pulse Coupled Neural Network PAPCNN)融合。PAPCNN不需要训练,仅通过迭代就可以捕获高频图像的边缘和细节。高频图像融合的公式如下:
Hhigh={Ihigh1,T1,j,j(N)>T2,i,j(N)Ihigh2,otherwise 。
其中,
Ihigh 是融合的高频图像,
T1,i,j(N) 、
T2,i,j(N) 表示经过N次迭代后高频图像1和高频图像2中神经元产生的点火次数。
Ihigh1 、
Ihigh2 为融合图像1与融合图像2的高频分量。最后,将融合的低频和高频图像进行NSST逆变换,得到增强的融合图像。
4. 实验结果与分析
为了验证本文算法的可行性和有效性,实验选取了六组全彩图像和可见光图像进行融合。本文算法与其他五种算法进行了比较,结果如图4~9所示。另外五种算法是小波算法、区域能量算法、HIS方法、NSST-PCNN和NSST-PCA。
从图中可以看到,小波算法和HIS方法得到的图像整体较暗,但小波算法图像的结构信息较好,HIS方法图像的空间结构信息损失较严重;区域能量算法得到的图像光谱信息保持较好,但图像边缘信息略差;NSST-PCNN方法得到的图像光谱信息保持较好,但图像有些失真;NSST-PCA方法得到的图像边缘较清晰,但是光谱较为失真;相比上述几种方法本文提出方法的图像的光谱信息和空间结构信息更优,本文算法具有较好的融合效果。
为了更好地评价图像的质量,本文采用5种客观评价指标对不同的图像进行客观评价,评价结果如表1所示。5种评价指标分别为熵值(Entropy, EN)、图像失真指数(NIQE)、平均梯度(Average Gradient, AG)、空间频率(Spatial Frequency, SF)和边缘强度(Edge Intensity, EI)。信息熵用于衡量融合图像的信息量,信息熵越高,融合图像质量越好。图像失真指数用于衡量融合图像的失真程度,图像失真指数越小,融合图像质量越好。平均梯度用于衡量融合图像的清晰程度,平均梯度越大,图像的清晰度越好,融合图像质量越好。空间频率指图像灰度的变化率,空间频率越大,融合图像质量越好。边缘强度指可识别边缘相对于背景的最小灰度差异,边缘强度越大,融合图像质量越好。为了更好地评价图像的质量,本文采用五种客观评价指标对不同的图像进行客观评价。
服务器出错,请稍后重试
Table 1. Experimental results analysis table
表1. 实验结果分析表
从表1中可以看出,为了客观、公正地评价融合图像,使用了五个客观评价指标进行评价。所提出的算法整体效果优于其他五种融合算法,这表明所提出的算法能够更好地突出图像的目标信息,更好地保留源图像的轮廓、细节和纹理信息,并提高了融合图像的对比度和清晰度。
5. 结论
由于遥感图像无法同时兼顾光谱信息和空间信息,因此,图像融合是平衡两者以提高图像质量的关键。传统的融合算法常常存在光谱失真、空间信息丢失或不适用于多个传感器等问题。为了上述问题,本文提出了一种将NFM与NSST相结合的遥感图像融合算法,该算法可以有效地保持边缘和纹理等细节信息。NSST在分解后没有方向数限制,在细节提取方面表现出色,可以更好地稀疏表示图像并减少复杂度。非负矩阵分解有效地减少了图像融合的空间和光谱失真现象,并挖掘了不同光谱波段之间的稀疏性。与其他算法相比,本文算法是一种有效的融合算法。实验结果表明,该融合方法取得了良好的融合效果。通过与其他图像融合方法进行主观与客观方面的评价比较,证明采用这种方法优于使用NSST-PCNN图像融合算法等其他几种方法,本文提出的融合算法将更多的空间细节信息保留了下来,而且融合图像具有较强的可视性。