1. 引言
锂离子动力电池具有使用寿命长、自放电率低以及能量密度高等优点,目前被广泛应用于新能源电动汽车、光伏储能、铁路基建等领域 [1] ,为了合理地利用动力电池,从而最大程度地延长动力电池生命周期,必须随时准确获取动力电池的真实状况,而动力电池的真实状况无法直接测量得到,只能通过动力电池管理系统(Battery Management System, BMS)中的动力电池模型的仿真估算 [2] [3] 。
锂电池的内部反应非常复杂,因此一般利用电压、电流、温度等这些外界特性,来推测电池荷电状况(State of Charge, SOC)、电池健康状态(State of Health, SOH)等。常用的电池模型,按照不同的形成机制包括电化学模型、等效电路模型以及神经网络模型。电化学模型着重分析电池在使用过程中的化学反应,模型复杂但准确度高 [4] ;等效电路模型通过电阻电容等常用元件经过串联和并联方式组成电路 [5] ;神经网络模型通过神经网络训练数量可观的实验样本,建立多个电池内外特性关系,模型精确但所需数据庞大且建立时间长 [6] 。应用于实际中时,一般会使用等效电路模型来辨识电池参数。相比于另外两种电池模型,等效电路模型的模型搭建较简单、参数辨识较容易且便于验证模型精确度。
在考虑仿真准确性和识别复杂性后,本文选择拥有两个RC回路和一个欧姆内阻的二阶RC模型作为电池等效电路模型(如图1),两个RC回路分别代表了电池的电化学极化和浓度差极化,欧姆内阻表示了电池的内阻特性,该模型相较于其他模型具有更高的模拟精度,参数辨识也较其他模型更为方便准确 [7] 。
由基尔霍夫定律可得二阶RC模型的电压和电流的关系式如下,式中U1和U2为两个RC回路的电压:
2. 锂离子电池特性
本文用于试验的电池是由深圳市威可力有限公司的LFP7570260锂离子电池,该电池规格参数如表1所示。

Table 1. Specifications of battery LFP7570260
表1. 电池LFP7570260的规格参数
OCV-SOC关系标定实验
锂离子电池特性实验有助于确定电池性能,为锂电池参数辨识模型的建立提供基本的实验数据。
电池开路电压(Open Circuit Voltage, OCV)是指电池在不接入回路情况下端电压的稳定值,是判断电池状态的主要依据之一。因为电池的OCV值会随着SOC的下降而减小,所以可以通过电池的OCV值来评价电池状态、标定电池SOC。电池可以在充放电过程中,通过充分静置的方式避免迟滞效应带来的影响,从而获取较准确的OCV值并用于对电池模型的仿真验证 [8] [9] [10] 。
具体实验步骤如下 [11] :
1) 以0.5 C电流(即5 A电流)恒流充电,当电池端电压为截止电压4.2 V时停止充电;
2) 将电池静置2分钟;
3) 再以4.2 V电压对电池恒压充电,当电池充电电流小于0.02 A时停止充电;
4) 将电池静置4小时,测量电池的端电压,近似于开路电压;
5) 以0.2 C电流(即2 A电流)恒流放电半小时,此时SOC值降低10%;
6) 将电池静置4小时,测量电池的端电压;
7) 重复步骤5)~6);
通过上述实验所得的资料,采用描点做图得到了OCV-SOC的拟合曲线,如图2所示。
3. 电池模型参数辨识及验证
3.1. 参数辨识模型
本文搭建的二阶RC等效电路模型的待辨识的参数有Em、R0、R1、C1、R2、C2,该电池模型如图3所示,将在室温环境下采集的电池电压、电流数据导入到参数辨识模型中,辨识函数为:
其中,U(t)是电池在t时刻的端电压,I是回路电流。
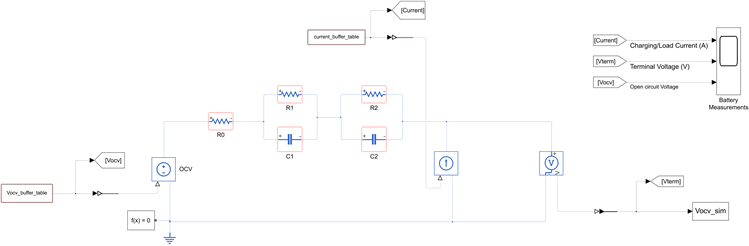
Figure 3. Identification model of second-order RC parameters for lithium batteries
图3. 锂电池二阶RC参数辨识模型
3.2. 参数辨识算法
最小二乘法(LS)是以函数模型模拟系统的过程中找出一组参数,使模拟输出电压与实际输出电压之间的偏差平方和达到最小值。
最小二乘法的估计值为:
,
为数据矩阵,Y为输出数据向量。
由于LS的计算工作量随着数据的增加而明显上升,文献 [12] 采用了递推最小二乘法(RLS),在每一次有新的观测数据时,利用新数据对上一时刻的LS估算结果再加以调整得出本次的估算结果,而不是再次重新计算最小二乘法的估计值。相较于LS简化了计算,内存资源消耗减小。
递推最小二乘的公式为:
其中,
为系统上一时刻估计值,
为系统当前时刻理论观测值,y(k)为实际观测值,K(k)为系统的增益矩阵,实际观测值与理论观测值相减作为系统的预测误差,再与增益相乘即可得到此刻预测值得校正,然后再加上系统上一时刻的估计值便能得到当前时刻估计值。
然而,RLS辨识算法在数据逐渐增加时,更容易产生“数据饱和”现象,新信息也易于被淹没。为了解决此缺陷,可以添加遗忘因子
,削弱对原有数据的权重,从而使得新数据的作用增强,这便是遗忘因子递推最小二乘法(FFRLS) [13] 。
遗忘因子递推最小二乘法的具体公式为:
式中,遗忘因子
取值范围在0~1,一般取0.9~1。
因为对电池模型采集的原始数据较多,为简化算法的计算,本文决定采用带遗忘因子的递推最小二乘法,
取0.95。
3.3. 参数辨识过程
采用GH 1 kW/1.5 kW Series可编程电源系统GH600-2.6,使电池按照电流脉冲工况运行,得到的电池放电电流、电压曲线如下图4、图5所示。
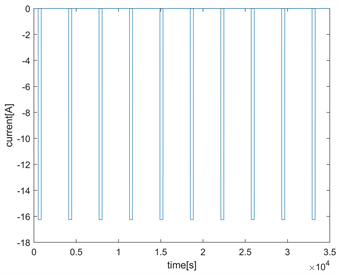
Figure 4. Current curve of battery external characteristics
图4. 电池外特性电流曲线
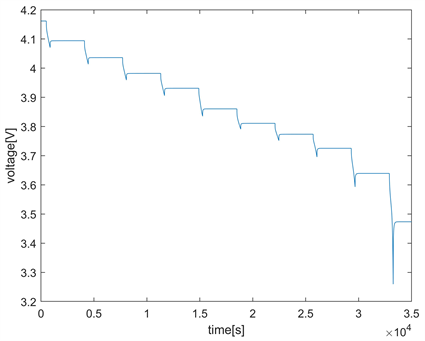
Figure 5. Voltage curve of battery external characteristics
图5. 电池外特性电压曲线
参数辨识过程:首先向辨识模型输入参数的初始值,电池模型在给定的电流工况下输出电压值,然后采用遗忘因子最小二乘法对参数加以修正,得到使当前输出电压值与当前实际电压值误差最小的参数,在不同时刻逐步地对模型的参数加以优化后得到最终的辨识参数 [14] 。
图6~11是参数辨识过程中的脉冲段1、5和10的端电压仿真结果与测量结果的波形对比,可以看出:优化后的仿真电压与实际电压间误差相比于优化前明显减小,表明电池模型的参数越来越精确。
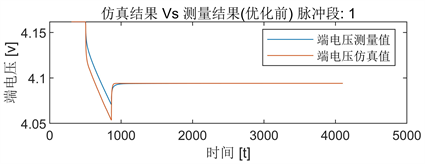
Figure 6. The simulated and measured terminal voltage before optimization of pulse segment 1
图6. 脉冲段1的优化前端电压仿真值与测量值
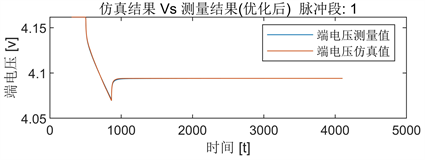
Figure 7. The simulated and measured terminal voltage after optimization of pulse segment 1
图7. 脉冲段1的优化后端电压仿真值与测量值
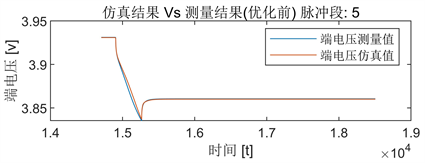
Figure 8. The simulated and measured terminal voltage before optimization of pulse segment 5
图8. 脉冲段5的优化前端电压仿真值与测量值
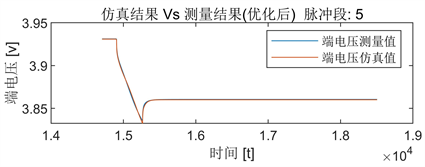
Figure 9. The simulated and measured terminal voltage after optimization of pulse segment 5
图9. 脉冲段5的优化后端电压仿真值与测量值

Figure 10. The simulated and measured terminal voltage before optimization of pulse segment 10
图10. 脉冲段10的优化前端电压仿真值与测量值
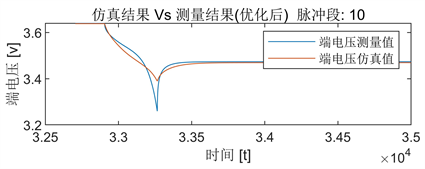
Figure 11. The simulated and measured terminal voltage after optimization of pulse segment 10
图11. 脉冲段10的优化后端电压仿真值与测量值
电池充放电数据辨识出的电池模型参数如图12~17所示。
3.4. 参数辨识结果验证
在计算机中,将参数辨识结果代入到二阶RC电路模型(图18)中,将验证工况电流值输入,模型的输出电压和实际电压对比结果如图19所示,最大误差小于4%,表明辨识的模型参数可信,验证所建立的二阶RC等效电路模型基本可以满足仿真需求。在放电末期误差相对增大,是因为电池在这个阶段极化现象严重,电压变化剧烈,同时化学反应更加复杂,得到的实验数据误差较大 [15] 。

Figure 19. Comparison of model output voltage and actual voltage
图19. 模型输出电压与实际电压对比
4. 结语
本文选择了使用较为普遍、参数识别有效且辨识误差较小的二阶RC等效电路模型,通过OCV-SOC关系标定实验、恒流充放电实验得到电池的相关数据,辨识电池等效模型中的有关参数,研究了一种动态调节电池模型参数的辨识方式,该辨识方式的工作量较少,且更新频次小,对电池管理精度高。通过对比电池实际电压值和模型输出电压值,表明其构建的电池等效模型可以模拟电池自身在恒流状态下的运行情况,表明该电池模型参数辨识方法可靠有效,但在放电末期模型误差增大,后续考虑增加RC模型阶数并优化辨识算法,提升电池模型辨识精度。
基金项目
江苏省研究生科研与实践创新计划项目(SJCX22_1713)、国家自然科学基金(61873346)、镇江市科技计划项目–产业前瞻与共性关键技术(GY2021017)。

