1. 引言
磨抛通常作为制造加工的最后一道工序,是提高零件表面完整性和尺寸精度、保证产品性能的关键技术。但是,机器人本身不具备柔顺性,无法适应复杂多变的外部环境,容易导致对工件的过磨抛和欠磨抛,因此必须对机器人末端与工件之间的磨抛力加以控制。同时,在实际磨抛加工中,不同的磨抛工艺参数也对零件表面质量有很大影响,选择合适的工艺参数组合对于降低工件表面粗糙度、提高磨抛效率至关重要。
针对机器人磨抛力控制,田勇等 [1] 通过MATLAB对阻抗控制中性能参数进行了仿真,得到最优参数组合,并利用自行设计的打磨系统进行实验验证,得到了良好的打磨跟随效果。Du等 [2] 基于位移控制的原理,结合自主研发的CAM/CAD处理器以及自适应抗饱和积分分离模糊PI控制器,针对钛合金材质工件进行磨抛仿真模拟和实验,得到了较好的磨抛效果。Fu等 [3] 提出了一种非线性PI位置控制器,有效的解决了积分饱和问题,对阻力产生的影响做出了补偿,进一步增强了磨抛的顺应性。高培阳等 [4] 在阻抗控制的基础上,结合自抗干扰控制,对力控制跟踪器加以改进,解决了打磨过程中的力冲击问题,增强了机器人的鲁棒性和适应能力。Pedrocchi等 [5] 提出了一种带有模糊调节器的阻抗控制回路,更好地实现了打磨过程的力的稳定性和质量一致性。
为了提高工件磨抛质量和效率,除了要进行力控制外,工艺参数的合适选择也是至关重要。在磨抛工艺参数方面,淮文博等 [6] 针对叶片工件,采用响应面法计算得到了抛光工艺参数优化组合和优化比值,利用正交试验建立了粗糙度预测模型,并进行了实验验证。Zhao等 [7] 在砂带抛光中,利用单因素试验获得了参数的优化范围,采用响应面法分析确定了优化工艺参数组合,从而有效降低了表面粗糙度。何瑛俏等 [8] 针对发动机叶片,建立了叶片型面的材料去除率模型,针对磨抛工艺进行研究和优化,通过实验证明了优化参数方案的可靠性。陈霖等 [9] 针对整体叶盘叶片,以材料去除深度为约束建立了磨抛过程材料去除率模型,从而得到最优工艺参数,实现了机器人的自适应磨削。Wang等 [10] 基于自主研制的小型抛光机器人系统,利用正交试验和灰色关联度分析方法对工艺参数进行了优化,得到了优化的抛光工艺参数组合,在保证粗糙度的前提下有效提升了磨抛效率在。Lee等 [11] 学者针对模具型腔五轴机器人抛光工艺,提出了基于特征提取和系统数据集成理论的表面抛光工艺规划技术,实现了加工工序和工艺步骤的高效化。
2. 末端力阻抗控制建模与仿真
2.1. 阻抗控制模型理论
阻抗控制是将末端执行器与环境间的作用关系定义为质量–阻尼–刚度模型,使用阻抗模型可以描述末端执行器与环境之间的力/位动态关系,在控制过程中,通过调节阻抗模型中的参数,可以改变机械结构末端与接触环境的力/位关系,进而将力和位置控制纳入同一控制体系中。阻抗控制的基本原理如图1所示:

Figure 1. Impedance control principle
图1. 阻抗控制基本原理
阻抗模型常用的三种形式为:
(2-1)
式中,
为阻抗控制惯性、阻尼、刚度系数;
是末端执行器在三维空间中实际加速度、速度、位移向量;
是末端执行器期望加速度、速度、位移向量;
是末端执行器与环境间的实际接触力。为了实现精准的力跟踪,引入一个期望力
,则上式可变为:
(2-2)
在阻抗控制中,令力偏差
,位置偏差
,位置X为恒定常数,即
,则有:
(2-3)
则阻抗模型为:
(2-4)
2.2. 末端磨抛力阻抗控制模型
根据阻抗控制理论构建末端执行力控制模型,如图2所示。根据控制模型,本文利用MATLAB/Simulink进行控制器的设计与仿真,其仿真框图如图3所示,采用PD控制器为力控制系统的运动控制器,依据阻抗公式(2-3),给定期望力
,在保持系统稳定的前提下,通过改变惯性参数、阻尼参数、刚度参数,探索阻抗参数对系统的影响,得到阻抗控制的控制规律。
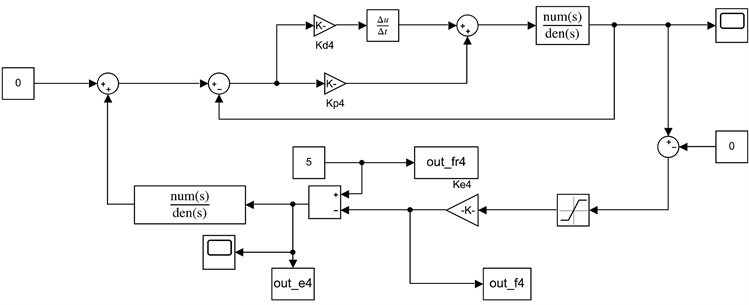
Figure 3. Impedance control simulation block diagram
图3. 阻抗控制仿真框图
2.3. 末端磨抛力阻抗控制性能仿真
2.3.1. 惯性参数对系统控制规律的影响
保持阻尼参数
,刚度参数
的数值不变,改变惯性参数的值分别为
,得到惯性参数对力误差的影响曲线如图4所示:惯性参数的值对系统静态误差影响较小;随着惯性参数的增大,系统响应的上升时间和调节时间会变短,但超调量会越大,达到稳态所需的时间越长。
2.3.2. 阻尼参数对系统控制规律的影响
保持惯性参数
,刚度参数
的数值不变,改变阻尼参数的值分别为
,得到阻尼参数对力误差的影响曲线如图5所示:改变阻尼参数时,调节时间会随着阻尼参数的增大而变短,超调震荡特性减弱;随着阻尼参数的值增大,误差出现零值时间减小,期望输出力更快达到设定力;系统的静态误差不受阻尼参数影响。
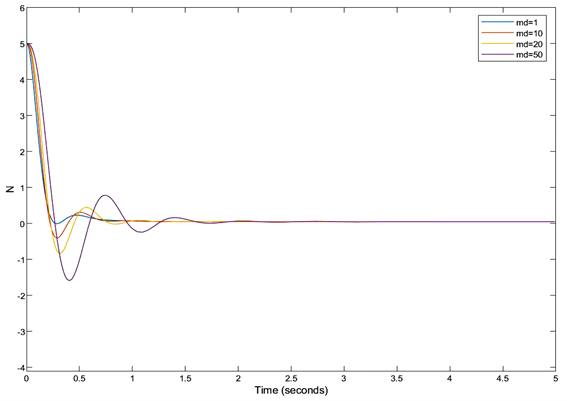
Figure 4. Influence curve of inertia parameters on force error
图4. 惯性参数对力误差影响曲线
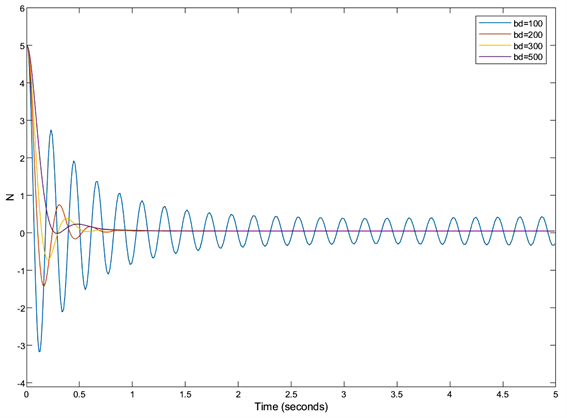
Figure 5. Influence curve of damping parameters on force error
图5. 阻尼参数对力误差影响曲线
2.3.3. 刚度参数对系统控制规律的影响
保持阻尼参数
,刚度参数
的值不变,改变阻尼参数的值分别为
,得到阻尼参数对力误差影响曲线如下图6所示:改变刚度参数的值时,系统的稳态误差值随刚度值的变化而变化;力控误差的稳态值随刚度参数增大而增大,说明刚度值的增大会导致期望力跟随实际力的能力变差;刚度系数的值越小,系统的力跟踪效果更好,磨抛工具柔性越好。
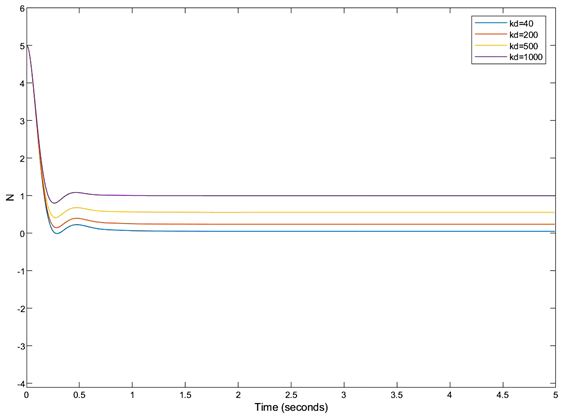
Figure 6. Influence curve of stiffness parameters on force error
图6. 刚度参数对力误差影响曲线
基于上述的影响规律研究,针对本实验装置选取惯性参数
,阻尼参数
,刚度参数
作为最优参数组合,以实现提高响应速度,降低力超调量,力尽快趋于稳定的目的;为了进一步提升磨抛的质量,在阻抗控制模型参数整定的基础上,需要进一步结合较好的机器人打磨工艺参数。
3. 工艺参数对表面粗糙度影响及优化
3.1. 机器人打磨工艺实验平台
为了探索工艺参数对表面粗糙度影响规律,本文采用铝合金平板作为试件进行磨抛工艺,尺寸为120 mm*120 mm*10 mm的工件利用台钳进行固定,台钳下面安装有Kistler测力仪采集打磨时工件受到的打磨力,保证力数据的绝对方向准确性。同时,KUKA机器人末端安装气动磨抛工具,从而实现对工件表面的磨抛。机器人磨抛过程中对工件进行定位,并采用局部坐标系对磨抛路径进行规划,实现磨抛过程中的磨抛深度的恒定,实验中路径规划在示教器中完成。磨抛完成后,利用泰勒–霍普森S-128粗糙度仪对工件进行检测,该粗糙度仪的性能参数如表1所示。

Table 1. Performance parameters of Taylor-Hopson roughness meter
表1. 泰勒–霍普森粗糙度仪性能参数
3.2. 单工艺参数对表面粗糙度影响分析
为了分析工艺参数对打磨表面质量的影响规律,首选采用单因素实验对主要的磨抛工艺参数进行分析,其中包括主轴转速、磨抛深度、进给速度、砂纸粒度。主轴转速决定磨抛中砂纸磨粒与工件之间的线速度,主要影响单位时间内接触工件的磨粒数量;磨抛深度代表弹簧压缩量,决定法向磨抛力大小,主要影响磨粒接触工件的深度与宽度;进给速度决定磨抛工具在工件表面停留的时间,主要影响磨粒产生作用的时间;砂纸粒度决定单位面积内磨粒的数量,主要影响磨抛过程中磨粒实际接触的总面积。
3.2.1. 主轴转速对工件表面粗糙度的影响
实验中,分别采用主轴转速为1000 r/min,2000 r/min,3000 r/min,4000 r/min,5000 r/min,6000 r/min进行实验,其实验参数如表2所示。

Table 2. Single factor experimental parameters of spindle speed
表2. 主轴转速单因素实验参数表
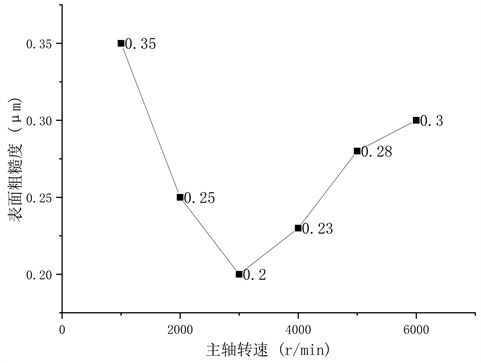
Figure 7. Experimental results influenced by single factor of spindle speed
图7. 主轴转速单因素影响实验结果
由结果图7可知,工件表面粗糙度随着主轴转速的增加先减小后增加,当主轴转速位于3000 r/min左右时,表面粗糙度值最小。当转速增大时,参与磨抛的磨粒数增多,材料去除速度加快,工件表面粗糙度降低;当转速继续增大时,由于转速过快,磨粒在工件表面停留时间过短,难以形成有效磨抛,所以材料去除低,表面粗糙度增大。
3.2.2. 进给速度对工件表面粗糙度的影响
实验中,分别采用进给速度为:0.005 m/s,0.007 m/s,0.009 m/s,0.011 m/s,0.013 m/s,0.015 m/s。其实验参数如表3所示。

Table 3. Single factor experimental parameters of feed speed
表3. 进给速度单因素实验参数表
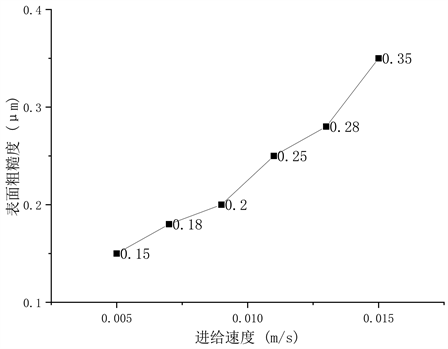
Figure 8. Experimental results influenced by single factor of feed speed
图8. 进给速度单因素影响实验结果
由实验结果图8可知,工件表面粗糙度随着进给速度的增加而增大。进给速度过大,单位数量磨粒作用时间减小,难以对工件产生有效的磨削,因此材料去除率低下,工件表面质量也随之降低。
3.2.3. 砂纸粒度对工件表面粗糙度的影响
实验中,分别采用砂纸粒度为:300#,400#,500#,600#,700#,800#。其实验参数如表4所示。

Table 4. Single factor test parameters of sandpaper grain size
表4. 砂纸粒度单因素实验参数表
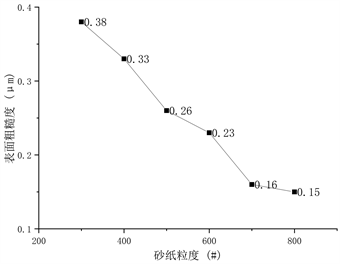
图9. 砂纸粒度单因素影响实验结果
由实验结果图9可知,随着砂纸粒度的增大,工件表面粗糙度减小。随着砂纸粒度的增大,砂纸单位面积内的磨粒数量增大,与工件接触的面积增大,可以产生有效的磨削,所以工件表面粗糙度明显降低。当砂纸粒度继续增大,单位面积内的磨粒数量过多,导致排屑困难,积聚在砂纸表面,影响磨粒与工件的直接接触,从而减弱砂纸的磨削性能,从实验结果曲线斜率也可看出,随着砂纸粒度的继续增大,粗糙度减小的程度也在逐步下降。
3.2.4. 磨抛深度对工件表面粗糙度的影响
实验中,分别采用磨抛深度为:0.3 mm,0.4 mm,0.5 mm,0.6 mm,0.7 mm,0.8 mm。其实验参数如表5所示。

Table 5. Single factor experimental parameters of grinding depth
表5. 磨抛深度单因素实验参数表
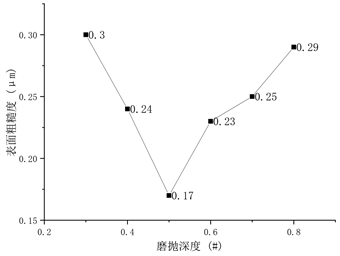
Figure 10. Single factor influencing the experimental results of grinding depth
图10. 磨抛深度单因素影响实验结果
由实验结果图10可知,工件表面粗糙度随着磨抛深度的增加先减小后增大。当磨抛深度增大时,磨粒可以与工件进行有效的结合,此时接触面积大,可进行充分的磨抛,材料去除率较高,工件表面质量好;随着磨抛深度的继续增大,沿法向方向的力继续增大,此时会出现磨抛装置剧烈颤抖,前进缓慢的现象,对机器人会产生一定的损害;与此同时,磨抛深度过大,产生的切屑不易排出,积聚在砂纸和工件之间,进而减小磨粒与工件的实际接触面积,造成材料去除率减小,工件表面粗糙度增大。
3.3. 正交试验与磨抛粗糙度预测建模
正交实验法是一种被广泛应用的研究多因素多水平的设计方法,它利用正交表来设计实验,本节采用四因素三水平正交实验来建立表面粗糙度预测模型。根据打磨工况条件确定工件磨抛中的各工艺信息的取值范围:进给速度为:0.3 m/min~0.9 m/min,主轴转速:2000~6000 r/min,磨抛深度:0.4~0.8 mm,砂纸粒度:400~800#,表6为实验的因素水平表,并得到磨抛表面粗糙度结果如表7所示。

Table 6. Level table of grinding and polishing experiment factors
表6. 磨抛实验因素水平表

Table 7. Grinding and polishing test results
表7. 磨抛实验结果
为分析工艺参数对表面粗糙度的耦合影响规律,对根据四个工艺参数建立工件表面粗糙度的预测模型,表面经验模型进行建模 [12] :
(3-1)
其中,
为进给速度,
为主轴转速,
为磨抛深度,
为砂纸粒度,
为指数,将本式进行转换,如下式所示,将上表的数据带入式中,可求得各项系数。
(3-2)
将上表的结果带入上式,通过多元回归得到
、
、
、
,则上式为:
(3-3)
故上式可写为:
(3-4)
利用复相关系数检验法对拟合效果进行检测,回归软件计算出复相关系数
,给定显著性水平
,工艺参数个数
,试验次数为9,经查表可知复相关系数的临界值
,
而且
接近于1,所以拟合效果显著。
3.4. 多工艺参数对表面粗糙度的影响规律
为了分析工艺参数对抛光力的耦合影响规律,利用响应面法,将其中两个工艺参数的零水平值带入上述公式,以另外两个工艺参数为变量并在试验范围内取值,可得到工艺参数对表面粗糙度的耦合影响规律。
由图11(a)、图11(c)可知,当磨抛深度S增大和砂纸粒度N增大时,磨抛力F增大,材料去除率增大,表面粗糙度减小;当磨抛深度S增大时,弹簧压缩量增大,与工件之间的作用力也随之增大,磨粒与工件接触面积增大,材料去除率增大,表面粗糙度进一步减小。
由图11(b)、图11(e)可知,当进给速度V0减小和砂纸粒度N增大时,表面粗糙度降低;当进给速度减小时,磨粒在工件表面停留时间长,可以形成有效磨削;砂纸粒度增大,单位面积的磨粒增多,作用面积增大,表面粗糙度进一步降低。
由图11(d)、图11(f)可知,当主轴转速Vf和磨粒N增大时,表面粗糙度减小;当主轴转速增大时,纱布上的磨粒离心力增大,与工件接触时的作用力随之增大,磨粒增多,总体磨抛力随之增大,材料去除率增大,表面粗糙度减小。
综上所述,在选定砂纸粒度的情况下,可通过改变转速来改善磨抛过程中的排屑情况,以便提高加工效率;由于工件表面的不平整会引起弹簧压缩量的增大或减小,进而影响磨抛力的大小,造成工件的过磨抛或欠磨抛,造成生产效率低下,必须结合磨抛力的控制。因此,采用工艺参数与力控制相结合的方法,可以进一步的提高生产效率,获取所需的表面质量。
4. 基于阻抗控制和工艺优化的主动柔顺实验
为了验证所设计的工艺参数与力控制相结合的机器人磨抛方式的有效性,利用上面所述实验平台对工件进行磨抛实验,采用阻抗控制整定后参数,结合工艺参数分析,选取以下工艺参数组合,如表8所示。

Table 8. Process parameters of workpiece polishing experiment
表8. 工件磨抛实验工艺参数
在设定工艺参数组合下,给定法向磨抛力
,然后利用所搭建的机器人磨抛实验平台进行有阻抗控制实验图12(a)和无阻抗控制实验图12(b),并进行对比,其磨抛法向力
结果如图12所示。
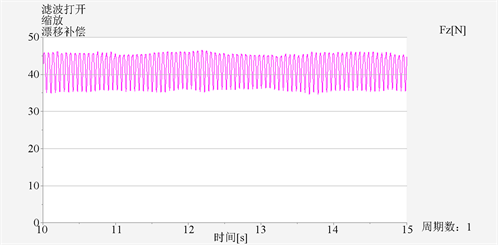
 (a)
(a)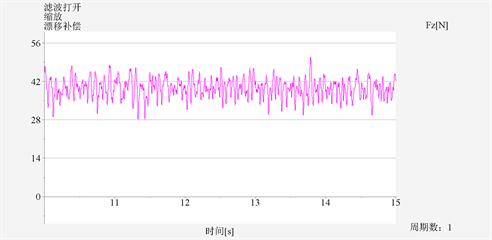
 (b)
(b)
Figure 12. Comparison of polishing force results with or without impedance control. (a) Grinding force and workpiece surface roughness under impedance control; (b) Polishing force and workpiece surface roughness without impedance control
图12. 有无阻抗控制下的磨抛力结果对比图。(a) 有阻抗控制下的磨抛力及工件表面粗糙度;(b) 无阻抗控制下的磨抛力及工件表面粗糙度
通过对上面的结果进行分析,(a)图所示,在阻抗控制下,磨抛力更加的稳定和均匀,在此基础上的工件表面粗糙度更小,完整度更高;(b)图所示,在无阻抗控制下,磨抛力变化幅度更大,杂乱无章,在加工中对工件造成一定程度的过磨抛或欠磨抛,影响工件表面质量。所以在生产过程,结合阻抗控制和粗糙度建模工艺参数优化的方法可以实现磨抛力的稳定控制,对获取理想表面质量具有重要作用。
5. 结语
本文首先通过对末端力阻抗控制系统建模与仿真、工艺参数对表面粗糙度影响实验与优化及优化研究,证明了末端力阻抗控制以及工艺参数对磨抛表面质量的重要性,并进一步结合阻抗控制和工艺参数优化实现磨抛质量的提升,主要研究成果如下:
1) 利用参数整定得到参数对控制规律影响,本实验中选取惯性参数
,阻尼参数
,刚度参数
组合,改善了控制力响应特性,提升了打磨的稳定性;
2) 工艺参数对磨抛表面粗糙度影响显著,可以通过影响因素分析建立表面粗糙度的预测模型,并得到的工艺参数优化组合;
3) 将工艺参数与力控制方法相结合,经试验验证,相较于无阻抗控制磨抛,有阻抗控制磨抛的工件表面粗糙度可进一步降低0.12 μm,进一步的提高加工质量及效率。
基金项目
国家自然科学基金青年项目(No.51905347);上海市科委科技创新行动计划高新技术领域项目(20511105704)。