1. 研究背景
2020年国内的制造业产出已经占到全世界的四分之一,但大多数制造业产品在全球价值链中所处的位置不高 [1] 。在过去几十年中主要依靠低成本劳动力和大规模生产来保持竞争力,而缺乏自主创新和高端技术。这导致了许多中国制造业企业只能从事低附加值的生产和加工业务,而难以在全球价值链中向上游和高端方向发展。现有阶段的国内的数控机床产业呈现出大而不强的发展格局,其中低端数控机床保有量巨大,高端数控机床自研率极低大部分依赖国外进口。
在曲面加工过程中,路径的光顺性会影响到加工表面的粗糙度与精度,可能会导致加工表面出现痕迹或者粗糙度不均匀的情况,从而影响加工件的质量和精度。为此Bi采用NURUS样条曲线对小段曲线进行拟合逼近 [2] ,并对五轴数控加工过程进行了全局拟合。Parouki等人 [3] 提出PH样条的弧长表示多项式样条函数,这使得算法可以在拐角位置进行光顺,使得弧长计算的效率与精确度得到了提高,提升了数控机床的加工效率。
切削力作为引起各轴运动的主要扰动源,算法设计中如果没有充分考虑将会对曲面加工精度造成较大的影响。切削力的大小和方向随着加工过程中材料的变形和去除而不断变化,因此需要进行实时监测和控制。在算法设计中,可以利用机床动态模型来预测切削力的变化,并通过控制机床轴运动来实现对切削力的控制。此外,为了提高曲面加工精度,还可以采用一些特殊的算法和工艺,如光滑路径规划、动态矫正等来减小切削力对曲面加工精度的影响。同时,选择合适的刀具和加工参数也是保证曲面加工精度的重要因素之一。从文献 [4] 可知通过控制进给速度可以使得金属材料的去除率与切削力保持在加工所需的最佳条件下,从而达到优化加工过程的目的。Erdim等人 [5] 从理论和实验上比较了基于磨削去除率和基于力的自由曲面三轴球头铣削进给速度调度策略。为了提高单轴跟踪误差,Tomizuka提出ZPETC [6] 控制算法,通过消除最小相位误差达到提升单轴控制精度的目的,此方案现已取得了实现与应用。AN Poo等人 [7] 提出了基于GCCC的轮廓误差补偿方法,该算法可以实现自有轮廓曲线的误差补偿。在交叉耦合控制方法中,可以采用多种控制器设计方法,如PID控制器、模型预测控制器等,以实现系统的稳定性和控制精度。同时,还可以采用一些特殊的技术,如模糊控制、神经网络控制等,来提高控制精度和稳定性。交叉耦合控制方法虽然可以在一定程度上提升轮廓误差控制精度,但在耦合控制器稳定性证明方面依然是个难题,还需要继续深入研究。
2. 速度规划算法
刀具轨迹优化是制造过程中的重要步骤,它可以提高加工效率、降低生产成本、减少加工时间和提高零件质量等方面的表现。在研究中,研究者关注的是高去除率下的切削力扰动,这是制约刀具轨迹优化的一个关键因素。在本研究中,总结和分析现有刀具轨迹优化方法,将高去除率下的切削力扰动作为限制条件。在算法设计过程中遵循“大误差速度优化,小误差轮廓补偿”的策略,有效地完成关键技术方案的设计。本文分析了现有的刀具轨迹优化方法,并将高去除率下的切削力扰动作为限制条件。数控程序汇含有工件加工刀尖位置与刀具方向指令,坐标为
,由于单轴伺服系统的存在跟踪误差,机床实际刀具坐标为
,刀具加工过程中的刀尖位置误差
与方向误差
是造成轮廓误差的主要原因,如图1所示。
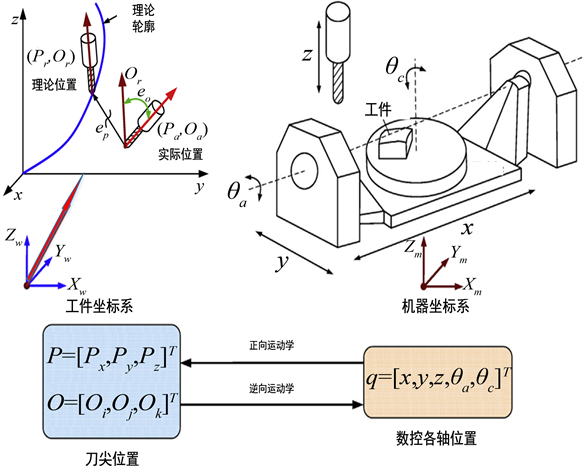
Figure 1. Relationship between tool motion path and each axis motion of five axis CNC lathe
图1. 刀具运动轨迹与五轴数控车床各轴运动关系图
刀具加工位置由数控机床各单轴运动形成,因此刀尖位置与刀具运动方向与五轴位移之间存在运动学关系模型,因此刀具的位置误差与刀具方向误差可转换成各轴的跟踪误差。刀尖位置误差与刀具方向误差可以用公式(1)进行表达:
(1)
公式(1)中:
代表刀尖位置误差;
代表刀具方向误差。
因此明确各轴的跟踪误差情况,就可以求解出刀具在加工过程中的刀尖位置误差与刀具方向误差。在单轴控制系统当中,系统的跟踪误来源于输入的轨迹指令与高去除率状态下的切削力扰动两部分。其误差传递函数可表达为:
(2)
公式(2)中:
代表输入信号的传递函数;
代表输入信号;
切削扰动信号传递函数;
代表切削力扰动。
但在高去除率状态下,单轴轨迹指令输入数据对于系统误差造成的影响较小,因此在实际优化算法的设计过程中主要考勤切削力扰动的影响,为此误差传递函数可表达为:
(3)
公式(3)中:
切削扰动信号传递函数;
代表切削力扰动。
为了更好的分析切削力扰动对与五轴加工误差的影响,设计过程将切削力影响情况通过数学函数关系式分别转化到各单轴的扭矩反馈,并设单轴误差为:
,进而推导出切削力与各轴跟踪误差曲线之间的关系如公式(4)所示:
(4)
公式(4)中:
各轴跟踪误差;
电机扰动力传递函数;
;
切削力与扭矩对应的雅可比矩阵;
高去除率状态下切削力扰动。
刀具加工过程中,各方向的瞬时切削力
在空间坐标系中的对用关系可以通过矩阵表达式进行表达因此在刀具速度优化算法的设置过程中各加工时段的速度优化曲线设计过程中,将刀尖位置误差与角度误差限定在范围内,可减小论文误差完成刀具进给速度曲线的设计。
(5)
公式(4)中:
各轴跟踪误差;
电机扰动信号传递函数;
:切削力扰动扭矩传递函数;
切削力与扭矩对应的雅可比矩阵;
高去除率状态下切削力扰动;通过优化公式(5)可以求得高去除率环境下的最优速度进给曲线,为了避免进给速度突变完成速度曲线优化后采用样条函数进行光顺处理。
3. 结果分析
为验证优化策略对S型工件进行速度优化,其中毛胚为树脂材料,加工过程中主轴转速为15,000 rpm,切削宽度为4 mm,切削厚度15 mm,加工曲线如图2所示。
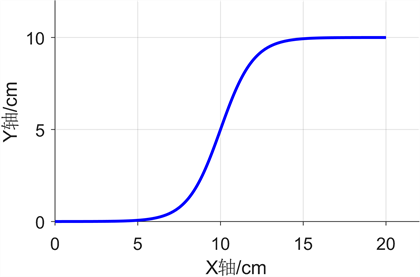
Figure 2. Machining curve of S-shaped parts
图2. S型零部件加工曲线
为了本文算法优势,将与恒定进给速度的数控加工过程进行对比。在实验中使用相同的切削工具和加工参数,并进行足够多的重复试验,以获得可靠的结果,如表1所示。

Table 1. Comparison of cutting methods
表1. 切削加工方法对比
4. 全文总结
在实验中使用相同的切削工具和加工参数,并进行足够多的重复试验,以获得可靠的结果。通过加工实例证明,进给速度优化加工时间约为60秒,加工效率提高20%以上。
基金项目
本文受到衢州市科技局:高去除率工艺下的五轴机床轮廓误差控制算法研究(ZD2022181)项目的资助。