1. 引言
生物质能源是国际公认的“零碳”可再生能源,已经成为世界上最主要的化石燃料的替代品之一。在双碳目标背景下,生物质能在中国发展现状呈现持续向好趋势 [1] 。生物质锅炉为主要的热能转化设备,锅炉温度作为评价设备运行状况的重要指标之一,其控制品质的好坏直接影响着锅炉的安全性和经济性。目前国内生产的生物质锅炉存在产能利用不充分、自动化程度低和排放不稳定等问题,严重阻碍了生物质锅炉的推广 [2] 。因此,改进生物质锅炉控制系统及其控制算法是提高生物质锅炉自动化程度和燃烧效率的关键。
生物质燃烧过程是一个非线性、强耦合的多变量延迟系统,有多个输入,如燃料供应、空气供应,以及多个输出,如加热功率、水温(热气温度)、炉膛压力,烟气中氧气或一氧化碳含量等。由于不同的生物质原料特性不同(水分含量,灰分含量,化学成分等),或者燃料批次不同,燃料水分含量的变化导致燃料能量含量的不确定性,使燃烧器的操作复杂化。传统PID控制存在控制参数整定不良、控制工况适应性差等缺点,在实际使用过程中受到一定的限制 [3] 。模糊控制不依赖于精确的数学模型,具有较强鲁棒性和适应性,但控制精度较低 [4] 。针对上述存在的控制难点,采用将常规PID控制与模糊控制相结合的控制策略能够明显提高系统的性能 [5] 。模糊自适应PID控制使系统具有较强的灵活性和抗干扰性,一定程度上提高了生物质锅炉的燃烧效率,满足高效清洁的燃烧要求,但不能很好地适应实际工业生产中复杂的工况环境 [6] 。内模控制能够消除干扰对系统的影响,改善时滞系统的控制品质 [7] 。
影响锅炉出水温度是否能够沿着预设值进行波动的关键变量就是送料量。而生物质成型燃料的热值差异以及送料速率的不同都会导致锅炉实际出水温度产生一定的波动,这种波动会使锅炉复杂的燃烧过程出现明显的滞后效果。本文通过比较模糊控制、PID控制以及内模控算法各自的优势,提出一种基于模糊自适应内模PID的控制方案,通过搭建实验平台建立锅炉出水温度控制系统的数学模型,并将这种控制策略应用到该控制系统当中。随后在MATLAB/SIMULINK平台上进行仿真分析,通过对比实验,确定生物质锅炉最优控制方法。
2. 锅炉温度系统的数学模型
生物质成型燃料锅炉工作过程如下:螺旋送料机将生物质成型颗粒送到炉膛的炉排上,在接收点火信号后点火器将炉排上的燃料点燃。生物质成型燃料受热之后逐渐蒸发出水分,伴随着温度的不断升高,燃料开始热解并析出大量的挥发分,焦炭逐渐被点燃并进入稳定燃烧状态,该过程成为热量的主要来源。锅炉水箱中的水作为传热介质吸收从化学能燃烧转化而成的热能,进而水温不断升高并达到设定温度。
锅炉的出水温度是评价锅炉运行状况的重要指标之一,体现了热量供需关系是否平衡,也体现了系统对外界负荷变化的响应速度。当锅炉温度的预设值不变时,而送料量、送风量或引风量出现自发性扰动时,控制系统应当能迅速消除这些扰动对系统稳定运行造成的干扰,维持锅炉出水温度稳定于预设值 [8] 。
从生物质成型燃料被送入炉膛到进入稳定燃烧放热阶段需要一定的时间,期间出水温度变化微小,此过程可以被视作延迟环节。当燃料燃烧进入稳定燃烧阶段,出水温度将会持续升高并最终稳定于设定值,此过程可以被视作惯性环节。因此根据其运行特点,生物质锅炉温度系统可近似为一阶惯性加纯滞后环节,传递函数如式(1)所示
(1)
式中:K为比例增益,τ为延迟时间,T为时间常数
考虑到温度控制系统的复杂性,本文采用系统辨识的方法测得系统运行过程中相关参数的动态数据,绘制动态响应曲线,并根据曲线特性获取相关参数,间接得到生物质成型燃料锅炉温度系统的数学模型。本次实验在新乡某生物质成型燃料锅炉厂进行,以锅炉水箱出水温度的预设值作为输入信号,根据出水温度实测值绘制响应曲线。具体流程为:首先将锅炉出水温度预设值由30℃调高至50℃,在此过程,分时段记录实际输出温度。如图1,利用graphical methods确定传递函数参数分别如式(2)、(3)、(4)、(5):
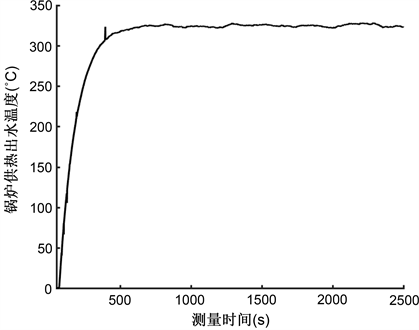
Figure 1. Temperature skyrocketing curve
图1. 温度飞升曲线
(2)
(3)
(4)
(5)
式中:
——系统稳定时的输出信号;
——系统稳定时的输入信号;
——平均滞留时间。
利用graphical methods可求得K = 5、T = 117、τ = 69,即系统数学模型为:
(6)
3. 模糊自适应内模PID设计
3.1. 常规PID控制
PID控制是一种运用比例、积分、微分对系统偏差进行处理的线性组合控制器。生物质锅炉温度控制器的任务就是保证出水温度稳定在预设值,且能够将控制过程中出现的各种干扰迅速消除,因而对控制品质要求较高,不允许被调量出现静差 [9] 。故选用PI控制,其算法表达式如下
(7)
式中:
——温度偏差、
——比例增益、
——积分增益。
其中传递函数形式如下:
(8)
PI控制结构如图2所示,PI控制参数好坏直接影响到生物质成型燃料锅炉温度控制系统的控制品质,因此选用合适的控制参数至关重要。
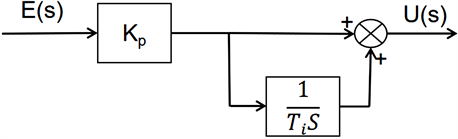
Figure 2. Conventional PI control structure
图2. 常规PI控制结构
3.2. 内模PI控制
3.2.1. 内模控制
内模控制是一种基于过程数学模型的新型控制策略,具有良好的跟踪指令以及抵消扰动影响的特点 [10] 。典型的内模控制结构如图3:
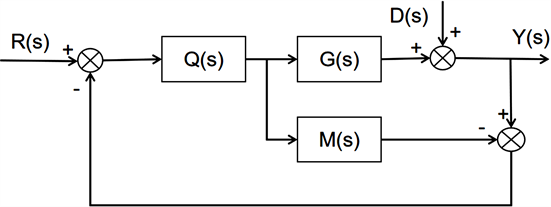
Figure 3. Internal mold control structure
图3. 内模控制结构
其中C(s)为被控过程对象,M(s)为内部模型(被控对象的数学模型),Q(s)为内模控制器,R(s)、Y(s)、D(s)分别为参考输入、过程输出、扰动输入。
实际过程中难以获得被控对象精确的数学模型,且被控对象含有惯性和时滞环节,所以设计中引入了滤波器f(s),可得
(9)
其中设
为G(s)中的最小相位部分,
,
为可调参数,
根据实际情况取值。
3.2.2. 一阶惯性加纯滞后系统的内模PI控制设计
一阶惯性加纯滞后系统的被控对象数学模型
(10)
将纯滞后环节进行Taylor展开,并取滤波器f(s)的阶次
,则可得内模控制
(11)
其中可将内模控制等效的转换成如图4所示的简单反馈系统
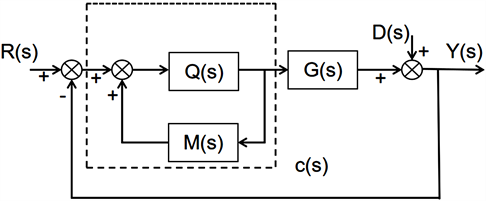
Figure 4. Internal model control system equivalent model
图4. 内模控制系统等效模型
其中虚线部分为反馈控制器,与内模控制Q(s)关系如下:
(12)
令理想PI控制器C(s)等于上式,可得
(13)
其中
(14)
3.3. 模糊自适应内模PI控制器设计
对于模型未知或难以确定的复杂控制系统,以及具有非线性、大时滞的控制对象,应用模糊规则及模糊集合,模拟人脑方式,进行模糊综合判断推理,解决以往常规方法难以处理的模糊性规则问题 [11] 。本文所设计的模糊自适应内模PI控制器能够实现模糊控制和内模PI控制优势互补。将模糊自适应内模PI控制器系统的预设值与实际输出之间偏差e及偏差变化率ec作为输入信号,利用模糊规则进行推理,获取不同时刻PI控制器参数Kp、Ki的修正量,即ΔKp、ΔKi,对生物质成型燃料锅炉温度实现准确地实时控制,提高系统的控制品质 [12] 。模糊自适应内模PI控制器结构如图5所示:
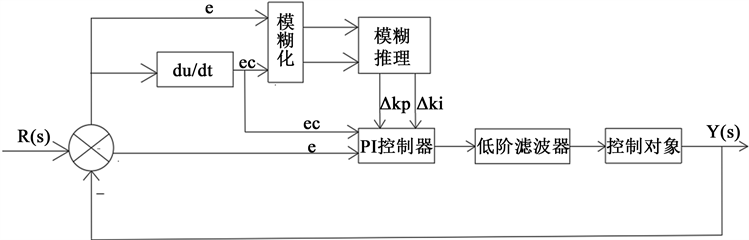
Figure 5. Fuzzy adaptive internal model PI control structure
图5. 模糊自适应内模PI控制结构
3.3.1. 隶属度函数建立
隶属度函数是模糊控制理论的基础,能否合理地构建隶属度函数是决定模糊控制效果优劣的关键。目前,并没有任何一套成熟有效的隶属度函数,大多确定方法都停留了在工程实践和经验积累的基础上。其中,三角形函数因其简单、易调整的特点成为了最为常用的隶属度函数。把温度设定值与实际输出值之间的偏差e及偏差变化率ec作为输入变量,内模PI控制器修正参数ΔKp、ΔKi,作为模糊控制器的输出变量 [13] 。将输入/输出变量进行模糊处理形成七个模糊集,分为{负大、负中、负小、零、正小、正中、正大},记为{NB、NM、NS、Z、PS、PM、PB}。设置输入、输出变量的模糊论域均为[−3, 3],由此可形成输入变量e、ec与输出变量ΔKp、ΔKi的隶属度函数曲线,如图6所示。
3.3.2. 模糊控制器规则和决策方法
模糊控制规则实际上是通过结合专家的知识和工程人员在的工作经验,定性分析输入量e、ec和输出量ΔKp、ΔKi之间的关系,总结得出的模糊控制规则,本设计采用49条模糊语言规则,如表1、表2所示。
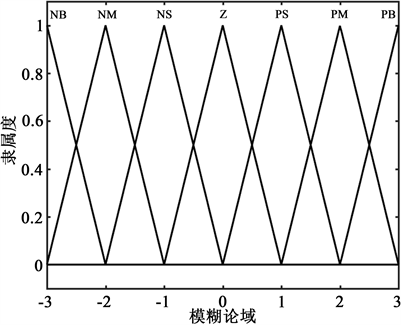
Figure 6. Input and output membership function curves
图6. 输入与输出隶属度函数曲线

Table 1. Fuzzy control rules for ΔKp
表1. ΔKp的模糊控制规则

Table 2. Fuzzy control rules for ΔKi
表2. ΔKi的模糊控制规则
模糊决策逻辑是模糊控制的核心,其中,Mamdani模糊推理算法是最简单、常见的方法。通过模糊推理得到仍是一个模糊集合,但在实际应用中,模糊控制需要一个确定值来驱动执行机构。因此,如何在推理的模糊集合中取出最具代表性的精确值成为了评价系统控制性能好坏的关键。最大隶属度函数不考虑输出隶属度函数的形状,只关心最大隶属度处的输出值,这样会丢失很多信息。因此,一般采用能够使推理控制获得更为平滑输出的重心法。重心法是将模糊隶属度函数曲线与横坐标围成面积的重心作为模糊推理输出的最终值。因此,模糊自适应内模PI控制器参数整定的实质是采用合适的模糊方法获得修正参数ΔKp、ΔKi对已确定的内模PI控制器参数Kp、Ki进行实时动态调整,相应的计算公式为:
(15)
(16)
模糊自适应内模PI控制器对在生物质成型燃料锅炉温度控制的流程如下图7所示:
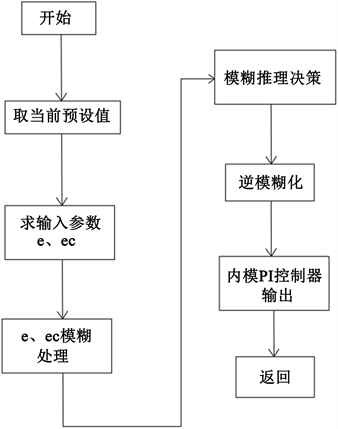
Figure 7. The progress of Fuzzy adaptive internal model PI controller
图7. 模糊自适应内模PI控制器的控制流程
4. 模糊自适应内模PI控制仿真
4.1. 仿真实验
本次实验以MATLAB软件为仿真平台,阶跃信号作为输入信号,分别采用常规PI控制、内模PI控制、复合模糊内模PI控制、以及本文所设计的模糊自适应内模PI控制在生物质成型燃料温度控制系统进行实验 [14] 。该控制系统的输出响应和时间与误差平方积分(ISTE)性能指标如下所示。
由图8和表3可知,常规PI时间与误差平方积分最大,调节时间最长。模糊内模PI时间与误差平方积分次之,超调量最大,但相对内模PI控制可以有效缩短调节时间。模糊自适应内模PI控制的时间与误差平方积分最小,表明相对于其他控制器,本文所设计的控制系统能够在控制大偏差的同时缩短调节时间。
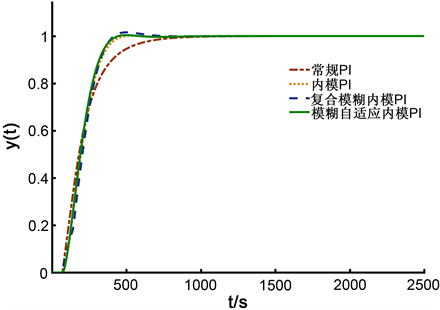
Figure 8. System output response curves under normal
图8. 正常工况下系统的响应曲线

Table 3. Performance ISTE indication of different control methods under normal
表3. 正常情况下不同控制方法的ISTE性能指标
4.2. 扰动实验
为验证生物质成型燃料锅炉温度系统在不同控制器下的抗干扰能力,在系统运行2000秒稳定且各控制参数不变的情况下,加入1%的阶跃干扰信号 [15] ,此时系统的输出曲线为
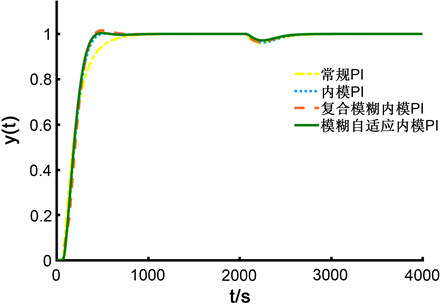
Figure 9. System output response curves under disturbance
图9. 扰动下系统的输出响应
由图9可知,系统在加入干扰后,常规PI、内模PI、模糊内模PI复合控制抗干扰能力较差,产生较大波动,而模糊自适应内模PI控制器抗干扰能力较强,能有效克服外界干扰的影响,能够使系统快速的恢复到稳定状态,提高系统稳定性。
5. 结论
本文以生物质成型燃料锅炉温度控制系统为研究对象,针对系统实际运行的非线性、大时滞、强耦合、多干扰等特点,对比常规PI响应速度慢、控制精度低、抗干扰性差的因素,综合分析各控制策略的优势性,提出了模糊自适应内模PI控制方法,并通过搭建Matlab仿真实验与其他控制策略进行比较。仿真控制结果表明,采用模糊自适应内模PI控制的生物质成型燃料锅炉温度系统具有响应速度快,超调量小,抗扰动能力强的特点,大大提高了系统的控制效率,改善控制品质,同时兼顾了系统的鲁棒性及稳定性。由于实际工业生产中普遍存在非线性、大时滞的复杂过程,因此该控制方法可应用于锅炉燃烧控制系统。
基金项目
《基于模型预测控制的生物质取暖炉排放智能控制系统研究》河南省国际科技合作项目(项目编号:232102521011)。
NOTES
*通讯作者。