基于势流理论的波浪能装置输出功率最大化研究

期刊菜单

基于势流理论的波浪能装置输出功率最大化研究
Study on the Maximum Output Power of Wave Energy Device Based on Potential Current Theory

DOI:10.12677/OJAV.2023.111001,PDF,HTML,XML,下载: 434浏览: 1,374
作者:屈帅镔,陈明浩^*,邵志锋,赵雅雯,陈航：南昌航空大学，飞行器工程学院，江西南昌
关键词:波浪能发电装置；势流理论；高阶偏微分方程组；拉普拉斯变换；局部遍历算法；Wave Energy Power Generation Device；Potential Flow Theory；Higher Order Partial Differential Equations；Laplace Transform；Local Traversal Algorithm

摘要: 过去，波浪能发电装置依照能量转换方式的不同可以分为三类：振荡水柱式、振荡体式、越浪式。目前，各国现有的波浪能海洋浮标普遍存在体积小、结构简单、供电低的缺点，导致生存能力和承载能力较差，大大限制了浮标的可靠性和应用范围。与大型波浪能装置或其他海上设施相比，振荡体类型体积小，耗电量少。海洋中有足够的波浪能来提取它。波浪动力浮标几乎可以部署在所有海域。因此，开发振荡体式波能发电装置是解决海洋浮标供电问题的有效途径。本文研究一种搭载PTO能量输出系统的振荡浮子式波浪能装置，在不同激励条件下的动能响应以及能量转换，并建立出一种普适性系统模型，并通过局部遍历寻优算法，得到系统最大功率时的阻尼C = 10,000。

Abstract: In the past, wave energy power generation devices can be divided into three types according to dif-ferent energy conversion modes: oscillating water column type, oscillating body type and overtop-ping type. At present, the existing wave energy buoys in various countries generally have the disadvantages of small size, simple structure and low power supply, resulting in poor viability and bearing capacity, which greatly limits the reliability and application range of buoys. Compared with large wave energy installations or other offshore facilities, the oscillating body type has small volume and low power consumption. There is enough wave energy in the ocean to extract it. Wave-dynamic buoys can be deployed in almost all sea areas. Therefore, the development of oscillatory wave energy power generation device is an effective way to solve the power supply problem of marine buoys. This paper studies the kinetic energy response and energy conversion of an oscillating float-type wave energy device with PTO energy output system under different excitation conditions, and establishes a universal system model, and obtains the damping C = 10,000 at the maximum power of the system through local ergodic optimization algorithm.

文章引用：屈帅镔, 陈明浩, 邵志锋, 赵雅雯, 陈航. 基于势流理论的波浪能装置输出功率最大化研究[J]. 声学与振动, 2023, 11(1): 1-8. https://doi.org/10.12677/OJAV.2023.111001

1. 引言

近年来，能源危机关系到国家安全，地球非再生能源逐渐枯竭以及环境状况日益恶化的形势下，如何高效利用资源充裕、可再生的海洋资源，已经成为各国和地区的普遍共识。《我国海洋能开发利用发展战略研究的基本思路》指出全球大部分海域的波浪能流密度属于可利用范围 [1]。而我国正处于波浪能落后的阶段，在波浪能领域的发电效率远远不如其他发电领域。但波浪能分布广泛、能量密度高，提示着我国必须重视其发展，而波浪能装置的能量转换效率是波浪能规模化利用的关键问题之一。目前的研究主要集中于实现波浪能发电系统的最大功率捕获问题，从PTO系统反作用力的控制角度可以分为无源阻尼控制与无功控制两种方法，其两种控制理论方法都有限定的适用范围，如波浪能发电装置的类型以及机械装置与波浪固有频率大小的限制 [2]。由王亚龙等人提出的波浪能发电装置结构优化显示波浪能收集装置对振荡水柱式波浪发电具有重要的意义和应用价值 [3]。

2. 波浪能装置数学模型建立

2.1. 垂荡纵摇浮子式波浪能装置介绍

如图1所示，为一种波浪能装置示意图，由浮子、振子、中轴以及能量输出系统(PTO，包括弹簧和阻尼器)构成，其中振子、中轴及PTO装置(如图2所示)被密封在浮子内部；浮子由质量均匀分布的圆柱壳体和圆锥壳体组成；中轴底座固定于隔层的中心位置，中轴架通过转轴铰接于中轴底座中心，中轴绕转轴转动，PTO系统连接振子和转轴架，并处于中轴与转轴所在的平面。除了直线阻尼器，在转轴上还安装了旋转阻尼器和扭转弹簧，直线阻尼器和旋转阻尼器共同做功输出能量。在波浪的作用下，浮子进行摇荡运动，并通过转轴及扭转弹簧和旋转阻尼器带动中轴转动。

浮体在波浪的作用下做摇荡运动时，会受到海水的作用，包括附加惯性力(矩)、兴波阻尼力(矩)和静水恢复力(矩) [4]。设定F_e水平面波动造成的波浪激励力，F_r为水平面兴波阻尼力，F_PTO为输出系统PTO力，F_hs为静水回复力，设m₁为浮子质量，m₂为振子质量，A为附加质量，设z₁为浮子垂荡位移，z₂为振子垂荡位移。

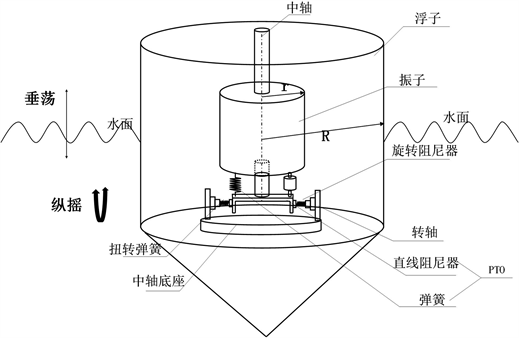
Figure 1. Heave and pitch float-type wave energy device

图1. 垂荡纵摇浮子式波浪能装置

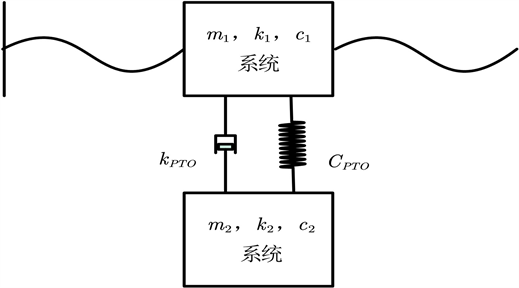
Figure 2. Schematic diagram of PTO device

图2. PTO装置示意图

1) 波浪激励力：海平面波浪对装置产生的周期性作用力

$F_{e} = F_{f} \cos ω t$ (1)

2) 兴波阻尼力：浮体在海水中做摇荡运动时，会兴起波浪，从而产生对浮体摇荡运动的阻力

$F_{r} (t) = γ \dot{z}$ (2)

3) PTO作用力：PTO装置中弹簧以及阻尼对装置的作用力

$F_{P T O} = k_{P T O} (z_{2} - z_{1}) + c_{P T O} ({\dot{z}}_{2} - {\dot{z}}_{1})$ (3)

4) 静水回复力：浮体在海水中做垂荡或者纵摇运动时，会受到使浮体回到平衡位置的作用力

$F_{h s} (t) = ρ g V (t)$ (4)

根据振子、浮子运动方式，可以得出静水中浮子的静止水面下的体积随时间的变化 $V (t)$ ，由后续求解可知浮子振幅小于1 m，静水恢复力在线性区间(圆柱区间)。因此静水恢复力有以下形式：

$V (t) = π R^{2} z_{1}$ (5)

将5)带入4)式中可得，

$F_{h s} (t) = ρ g π R^{2} z_{1}$ (6)

根据浮子运动状态可知，此外，由于推动浮体做摇荡运动的力不仅要推动浮体运动，还要推动浮体周围的流体运动，因而要使浮体在海水中获得加速度，需要施加额外的力，即为附加惯性力。对应牛顿方程中惯性质量的增加A。

2.2. 浮子、振子运动模型

对振子和浮子分别做受力分析如图3所示：

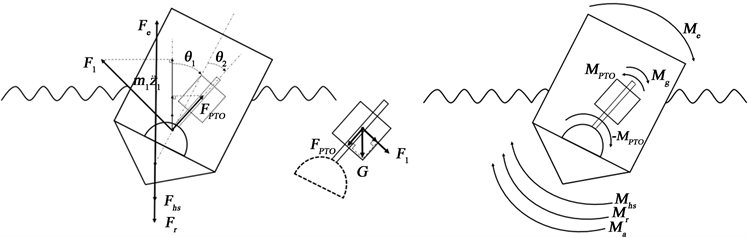
Figure 3. Force analysis of vibrator and float

图3. 振子、浮子受力分析

振子受力分析：

${\begin{cases} 振子重力 G = m_{2} g \\ PTO 装置作用力 F_{P T O} = k_{P T O} z_{2} + c_{P T O} {\dot{z}}_{2} \\ 振子与浮子垂直于中轴方向的相互作用力 F_{1} \end{cases}$ (7)

沿中轴运动方向运动方程为：

$m_{2} [{\ddot{z}}_{1} \cos (θ_{1} + θ_{2}) + {\ddot{z}}_{2} - z_{2} ({\dot{θ}}_{1}) + {({\dot{θ}}_{2})}^{2}] = k_{P T O} (z_{1} - l) + C_{P T O} {\dot{z}}_{2} + m_{2} g \cos (θ_{1} + θ_{2})$ (8)

垂直中轴运动方向方程为：

$m_{2} [- {\ddot{z}}_{1} \sin (θ_{1} + θ_{2}) + 2 {\dot{z}}_{2} ({\dot{θ}}_{1} + {\dot{θ}}_{2}) + z_{2} ({\ddot{θ}}_{1} + {\ddot{θ}}_{2})] = F_{1} - m_{2} g \cos (θ_{1} + θ_{2})$ (9)

浮子受力分析：对于浮子，只考虑竖直方向的垂荡运动。我们将振子重力项并入PTO装置弹簧恢复力，浮子重力项并入静水恢复力中，综上得竖直方向力为：

${\begin{cases} 波浪激励力 F_{e} = F_{f} \cos ω t \\ PTO 装置作用力分力 F_{P T O} = k_{P T O} (z_{1} - l + m_{2} g / k) \cos (θ_{1} + θ_{2}) + c_{P T O} {\dot{z}}_{2} \cos (θ_{1} + θ_{2}) \\ 静水恢复力 F_{h s} = ρ g π R^{2} z_{1} \\ 振子作用力分力 F_{1} \sin (θ_{1} + θ_{2}) \\ 兴波阻尼力 F_{r} = γ {\dot{z}}_{1} \\ 附加惯性力 F_{a} = A {\ddot{z}}_{1} \end{cases}$ (10)

波浪能装置转动惯量计算：

振子对转轴的转动惯量：

$I_{2} = \frac{m_{2} r^{2}}{4} + \frac{m_{2} h^{2}}{12} + m_{2} z_{2}^{2}$ (11)

浮子外壳对转轴的转动惯量：圆柱高度H₁、圆锥高度H₂

$I_{1} = \frac{2 π R H_{1}}{π R L + 2 π R H_{1}} m_{1} (\frac{R^{2}}{2} + \frac{H_{1}^{3}}{3}) + \frac{π R L}{π R L + 2 π R H_{1}} m_{1} (\frac{H_{2}^{2}}{6} + \frac{R^{2}}{4})$ (12)

振子转矩受力分析：

${\begin{cases} PTO 装置的扭矩 M_{P T O} = k_{m} θ_{2} + c_{m} {\dot{θ}}_{2} \\ 振子重力力矩 M_{g} = m g z_{2} \sin (θ_{1} + θ_{2}) \end{cases}$ (13)

浮子受力分析：

${\begin{cases} PTO 装置的扭矩 M_{P T O} = - (k_{m} θ_{2} + c_{m} {\dot{θ}}_{2}) \\ 静水恢复力矩 M_{h s} = ρ g π R^{2} θ_{1} \\ 兴波阻尼力矩 M_{r} = r_{m} {\dot{θ}}_{1} \\ 附加惯性力矩 M_{a} = I_{1} {\ddot{θ}}_{2} \\ 波浪激励力矩 M_{e} = L \cos (ω t) \end{cases}$ (14)

装置初始状态方程：

${\begin{cases} z_{2} (0) = l - \frac{m g}{k} \\ z_{1} (0) = {\dot{z}}_{1} (0) = {\dot{z}}_{2} (0) = 0 \\ θ_{1} (0) = θ_{2} (0) = {\dot{θ}}_{1} (0) = {\dot{θ}}_{2} (0) = 0 \end{cases}$ (15)

3. 数值计算

3.1. 势流理论模型假设成立条件

据上文中建立的势流理论模型求解波浪能装置整体基于海平面的静止状态特征，假设：

1、将海平面作为参考系；

2、设置垂直于海平面竖直向上为竖直正方向；

3、浮子初始振荡频率与波浪激励振动频率相同，无滞后状态；

3.2. 垂荡/纵摇浮子系统运动状态计算

将式(15)经过拉普拉斯变换求解得到高阶偏微分方程组，运用数值计算软件中计算，解出浮子和振子在波浪激励力 $f \cos ω t$ (f为波浪激励力振幅， $ω$ 为波浪频率)作用下前40个波浪周期内时间间隔为0.2 s的垂荡位移和速度以及纵摇角位移和角速度，再将t = 10 s、20 s、40 s、60 s、100 s带入式子中，得到下列数据，如表1、表2所示。

利用编程软件解出的结果导出为可视化的图像，有利于直观地展示其中的关系，如图4、图5所示。

Table 1. Table of heave displacement and velocity of float and vibrator

表1. 浮子和振子的垂荡位移和速度表

Table 2. Pitch angular displacement and angular velocity of float and vibrator

表2. 浮子和振子的纵摇角位移和角速度表

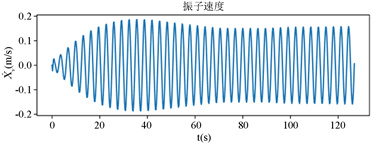
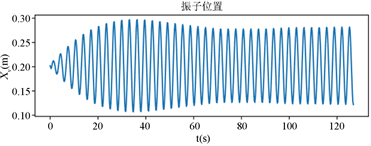
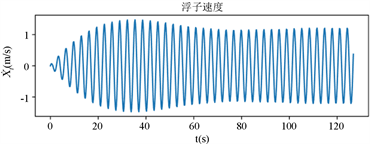
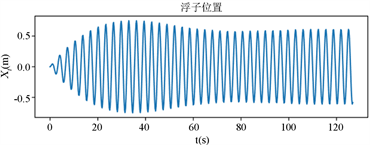
Figure 4. Time chart of vibrator and float movement

图4. 振子与浮子运动时间图

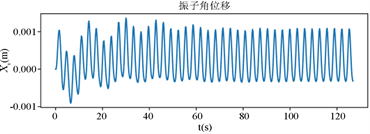
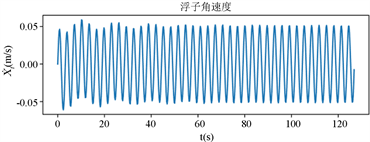
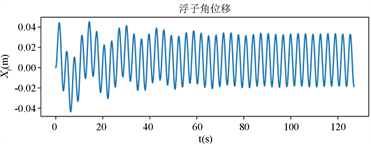
Figure 5. Rotation time diagram of vibrator and float

图5. 振子与浮子转动时间图

3.3. 浮子最大功率计算

在先前的研究中，PTO系统可以是直线电机或液压PTO系统，以液压PTO系统为例，系统中的蓄能器、油液刚度等要素决定了系统刚度k_pto，通常k_pto的选取主要考虑减少系统内部流量、压力波动，其作为储能元件不参与能量吸收 [4]。而该PTO系统中则主要以阻尼装置作为功率转化输出系统，取浮子为研究对象，建立其运动方程，得到其功率计算方程：

$P (i ω) = P_{θ} + P_{z} = \frac{1}{2} ω^{2} c_{P T O} {(| z_{1} | - | z_{2} |)}^{2} + \frac{1}{2} ω^{2} c_{m} (| θ_{1} | - | θ_{2} |)$ (16)

同时运用局部遍历算法进行计算，考虑浮子在波浪中只做垂荡和纵摇的情形，针对直线阻尼器和旋转阻尼器的阻尼系数均为常量且为相同值的情况，当直线阻尼器和旋转阻尼器的阻尼系数均在区间[0,100000]内取值，计算出最大输出功率及相应的最优阻尼系数为1000，如图6所示。同时还可以看出随着时间变换，其功率会呈现一个震荡的状态，但在高阻尼处的平均功率明显大于低阻尼状态。

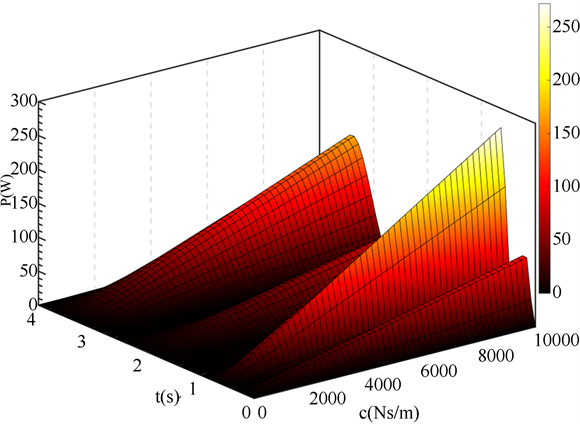
Figure 6. Time relationship diagram of output power-PTO device damping coefficient

图6. 输出功率-PTO装置阻尼系数时间关系图

同时得出最大输出功率时浮子、振子的运动状态，如图7所示：

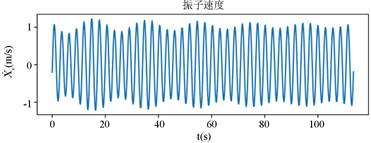
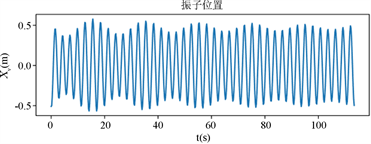
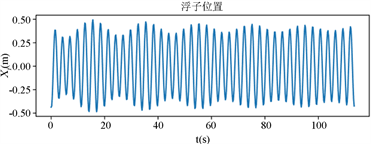
Figure 7. Stable motion state of vibrator and float under maximum output power

图7. 最大输出功率状态下振子和浮子的稳定运动状态

4. 总结

本文对于垂荡纵摇振荡体式波浪能装置进行数学动力学模型建立，分析了装置随波浪的运动特性以及PTO装置输出功率的影响因素，并计算出波浪能装置最大输出功率状态下的阻尼系数以及振子和浮子的稳定运动状态，发现此时振子和浮子的运动状态近似呈现“拍振”，即振子和浮子运动频率很相近时PTO装置的输出功率最大。蓸雪玲等人基于流体仿真软件对振荡浮子式波浪能发电设备的运动特性进行研究，分析不同阻尼工况的运动情况并进行数值模拟、实验验证 [5]。相较于该种方法，本文模型分析方法具有更好的适用性，不仅能够分析PTO装置对波浪能的利用，也适合被用来简单地分析所有振子–浮子系统组合形成的水面设施。验证了垂荡纵摇振荡体式波浪能输出装置发电方案的可行性，为未来波浪能装置输出功率提升提供理论依据。

参考文献

[1]	赵世明, 刘富铀, 张俊海, 张智慧, 白杨, 张榕. 我国海洋能开发利用发展战略研究的基本思路[J]. 海洋技术, 2008, 27(3): 80-83.
[2]	陈佳, 兰飞, 郭昊霖, 黎静华. 波浪能发电控制技术研究综述[J/OL]. 电力自动化设备: 1-20. https://kns.cnki.net/kcms/detail/detail.aspx?doi=10.16081/j.epae.202208025, 2023-01-09.
[3]	王亚龙, 尹广斌, 尹胜军, 于金龙, 李倩. 振荡水柱式波浪发电的波能收集结构优化研究[J]. 水电与新能源, 2022, 36(9): 27-32. https://doi.org/10.13622/j.cnki.cn42-1800/tv.1671-3354.2022.09.007
[4]	张增宝. 振荡浮子式波浪能发电系统捕能功率预测与多目标优化[D]: [硕士学位论文]. 济南: 山东大学, 2020. https://doi.org/10.27272/d.cnki.gshdu.2020.002730
[5]	曹雪玲, 高涛, 王文胜, 唐伟炜, 吕志胜. 单浮筒振荡浮子式波浪能装置的动力特性分析[J]. 太阳能学报, 2022, 43(11): 364-368. https://doi.org/10.19912/j.0254-0096.tynxb.2021-1232

为你推荐

January 3-5, 2017
Bangkok, Thailand

友情链接