1. 引言
反源问题在天线合成、医学诊断和地震监测等科学领域和工程应用中都有着非常广泛的应用 [1] [2] 。它是从波场数据确定未知点源的某些参数,如个数、位置和强度等。许多研究者从理论和数值的角度对源的重建进行了讨论 [3] [4] 。然而,反源问题的解通常不是唯一的,因此人们通常将源项限制在一些理想模型中。文献 [5] 给出了一种实时重建多运动点/偶极子源的代数方法。Chen等 [6] 提出了改进基本解方法,并在数值模拟中考虑了多个静止点源和一个移动点源的重建问题,然而这个方法受到点源之间距离的限制,对于距离较近的两个点源重建成一个源点。Zhang等 [7] 通过向反源系统添加一些参考点源作为额外的人工源来恢复辐射场,然后使用傅里叶方法求解无相位信息的多频反源问题。Wang等 [8] 对于Lamé系统中的矩张量点源,提出了一些新的采样型数值方案,这个方法的精度依赖于采样网格的选取。
近年来,神经网络方法被广泛应用于反问题的求解 [9] [10] [11] 。张平等 [12] 基于神经网络和门控思想构建点源位置参数反演模型,求解单频声波反源问题,数值实验说明点源之间距离的大小对反演结果影响较为微弱。陈柳 [13] 基于深度神经网络模型,预测恢复出区域内的源函数。Zhang等 [14] 使用神经网络设计了一个参数反演模型,通过声波场数据来识别和预测移动点源的轨迹。本文针对弹性波反源问题,构建基于全连接神经网络的点源位置和强度参数反演模型,从相关的远场数据确定有限数量的点源位置和强度信息。这个方法的优点是简单易实现,同时噪声水平测试和有限观测孔径实验说明模型具有很好的鲁棒性。
2. 弹性波反源问题
考虑二维弹性波反源问题,在各向同性均匀介质中来自源项
的弹性波场
满足Lamé系统:
(1)
这里
,
为Lamé常数,满足
,
,
为弹性波的角频率。在物理上,弹性波场
具有以下分解形式
其中
和
分别为p-波和s-波,且满足Kupradze-Sommerfeld辐射条件
(2)
这里
,
和
分别为p-波波数和s-波波数,且有
假设方程(1)中源项
由有限数量的分离良好的点源组成,可以表示为
(3)
其中
为Dirac分布,
表示第j个源的强度,
表示第j个源的位置,
,N是点源的个数。此外,散射场
在无穷远处有以下渐近形式:
(4)
其中
表示观测方向,i表示虚数单位,
和
分别表示
和
的远场模式。反源问题是根据固定频率的远场数据
和
,确定源的位置
和强度
。
3. 神经网络模型
建立求解弹性波点源位置和强度反演问题的神经网络模型。首先给出以下符号说明。
说明1:
表示观测方向的离散集,其中
是观测点个数。给定源的位置和强度,我们
得到观测的远场数据记作
(5)
其中
说明2:假设第j个点源的位置为
,对应的强度为
,
,点源的信息参数记作
(6)
其中
N是点源的个数。
于是,可将利用远场数据反演点源位置和强度转化为反演参数
的问题。
构建模型
以
和
为输入、输出,构建一个基于全连接神经网络的
参数反演模型,其中神经网络的隐藏层层数为2,结构如图1所示。
为了计算方便,假设
分别为输入层、隐藏层和输出层的节点,参数
表示节点
和
之间的权值,参数
表示
对应的偏置,其中
,记
那么,全连接神经网络可以写作
(7)
其中
表示激活函数,这里使用ReLU函数作为隐藏层中的激活函数
。
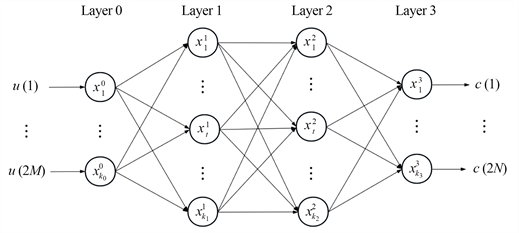
Figure 1. Structure diagram of fully connected neural network
图1. 全连接神经网络结构图
假设
为模型的真实输出,
为模型的预测输出,
则通过平方误差定义的损失函数为
(8)
更新模型就是更新模型中的权重和偏置,使用Adam优化算法更新模型。
至此,本文构建了反演点源位置和强度参数的神经网络模型。最后,给出重建方案的算法。
4. 数值实验
通过数值实验说明模型可以有效解决点源位置和强度反演问题,并使用带有噪声的远场数据进行数值实验证明模型的有效性和鲁棒性。
在所有的数值例子中,Lamé常数取
,
,并选择以原点为中心半径
的圆为测量曲线
,在
上从与x轴正半轴的交点开始逆时针均匀分布10个测量点。神经网络的一些参数设置如表1所示,这些参数的取值是通过多次实验得到的,并且参考了文献 [9] [10] [12] [14] 。

Table 1. Parameter setting of neural network
表1. 神经网络的参数设置
4.1. 单点源位置和强度的反演
根据测量的远场数据,分别反演强度随机、位于不同象限的4个单点源位置和强度,反演结果如表2所示。

Table 2. Inversion of the location and intensity of four single point sources
表2. 4个单点源位置和强度的反演
表2分别给出了真实源和重构源的具体值,以及二者之间的相对误差。从表2中可以看到,4个点源的位置和强度有较好的反演效果。这说明点源的位置不会影响模型的反演。
4.2. 多点源位置和强度的反演
在实验4.1的基础上,反演强度随机、位于不同位置的多点源位置和强度。3个点源和7个点源的位置和强度反演效果见表3和表4。

Table 3. Inversion of location and intensity of three point sources
表3. 3个点源位置和强度的反演

Table 4. Inversion of location and intensity of seven point sources
表4. 7个点源位置和强度的反演
从表3和表4可以看到多点源位置和强度反演的相对误差均控制在0%~2.3%之间。对比表2可以说明:点源个数的增加,不影响模型反演结果的准确性。
4.3. 噪声水平测试
在本实验中,对实验4.2中3个点源的测量数据加入不同水平的噪声,来测试模型的稳定性。在数据中添加一些随机扰动,则噪声数据表示为
其中
表示噪声水平,
是一个由均匀分布产生的随机数
。噪声水平
分别选取5%、10%和20%。

Table 5. Test of different noise levels for point source location and intensity inversion
表5. 点源位置和强度反演的不同噪声水平测试
从表5中可以清晰的看到,随着噪声水平的增加,重构的结果逐渐变差,相对误差也随之增加。与表3中点源真实的位置和强度对比,噪声水平越大反演的源的位置距离真实位置越远。加10%以下噪声时对位置和强度的反演结果无明显影响;当噪声水平增加到20%时,反演的位置和强度偏离真实值。模型具有一定稳定性。
4.4. 有限观测孔径测试
通常在实际应用中全孔径测量远场数据是会受到限制的,往往只能在有限的观测点收集远场数据。
本实验以实验4.2中3个点源的位置和强度为例,观测孔径分别取为
,
和
。为了比
较源位置和强度反演准确度,图2给出了不同观测孔径下位置和强度的反演效果图。
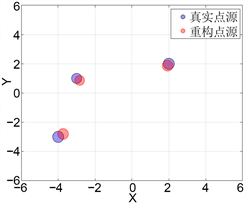
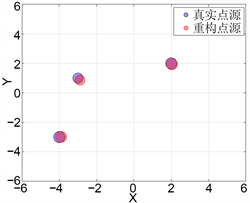
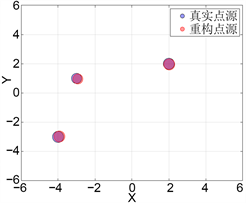
Figure 2. Inversion of point source location and intensity under different observation apertures
图2. 不同观测孔径下点源位置和强度反演
图2中圆点所在的位置代表源的位置,圆点的半径大小代表源强度的模。由图2可知:当观测点位置不变时,随着观测孔径的减小,观测点个数减少,导致从远场数据中获取的点源位置和强度信息减少,使得位置和强度参数的反演误差增大,反演效果降低。对位于第一象限的点源来说,观测孔径在减少,但反演需要的信息获取的足够多,所以这个点的反演效果明显优于其他源。
5. 结论
本文针对弹性波反源问题,构建了基于全连接神经网络的点源位置和强度参数反演模型,根据测量的远场数据反演点源的位置和强度。数值实验表明该模型效果良好,并且具有一定的鲁棒性。在以后的工作,我们将会考虑更加复杂的情况,例如移动点源的反演。
NOTES
*通讯作者。