1. 引言
输电塔是风敏结构,其风振响应是从业人员的关注点。然而传统方法在计算风振响应时十分复杂。
目前,国内外学者对输电塔风振系数计算的研究很多。蔡熠通过研究发现增加横隔面支撑可以提高输电塔的结构强度 [1] 。刘荣见等人通过试验发现
随着高度的增加而增大,但在分叉后会因为质量和刚度的减小而减小 [2] 。赵建等人通过数值模拟的手段发现虽然
沿高度呈线性分布,但在横担附近存在较大突变,且沿长悬臂方向变化幅度不大 [3] 。张爽等人通过有限元建模,研究不同风速、风向和塔型对输电塔风振系数的影响,得到输电塔塔身及横担对风振系数的影响 [4] 。赵爽等人通过对气动弹性模型的风洞试验,研究了超高层输电塔的ESWL (等效静力风荷载) [5] 。同时,分析了钢管混凝土和梯度风高度对
的影响,并对中国规范中设计风荷载公式的适用性提出了一些建议。

Figure 1. Transmission towers with cantilever cross-arms
图1. 悬臂输电塔
本文在此提出一种输电塔风振系数实用计算方法,该方法考虑了横担和法兰盘对风振特性的影响,与现有规范和有限元计算分析相比,具有计算结果更准确、计算过程更简洁的优势。首先建立形状均匀的输电塔计算模型,然后将形状变化的因素以及横担和法兰盘的影响引入到模型中,接着根据实际结构提出了一种新的输电塔设计风荷载计算模型。通过一系列简化,最终得到悬臂输电塔风振系数实用计算方法(如图1所示)。
2. 风振系数推导
输电塔由横担、法兰盘和主塔身组成,建立如图2所示的计算模型。
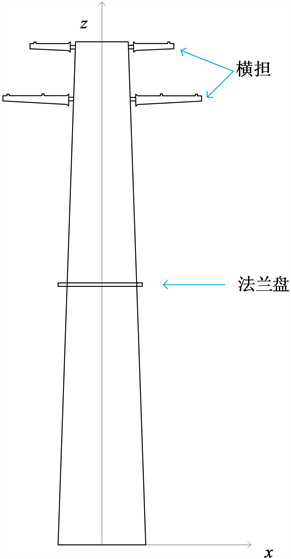
Figure 2. Legend of transmission tower calculation model
图2. 输电塔计算模型图例
首先需确定两个假设:其一,输电塔设计采用塔线分离法,这种方式更为保守 [6] 。其二,顺风方向的风振系数只能激发该方向的风振。
对于高层塔结构,风振惯性荷载为:
, (1)
其中,
是一阶模态的无阻尼自然圆频率;
是单位高度的质量;
是一阶模态的振型;
是
的标准偏差;
是一阶模态的时变广义坐标。
等效静力风荷载的总和(ESWLs):
, (2)
, (3)
其中
是单位高度沿风向的时变风阻力平均分量。
是z = 10 m时的平均风压;
是风压高度变化系数;
是局部阻力系数;
是局部有效挡风玻璃宽度;
是风振引起的动力系数;
与风的波动特性有关,称为综合影响系数;
与计算点的位置相关,可称为位置系数。公式(1)至(3)是ESWL的通用公式,适用于任何输电塔。由于公式中涉及的参数多、含有多重积分使其在实际使用中不便。
形状均匀的输电塔的质量和挡风面积在纵向上是不变的。因此,
、
、
和
是常数,且z = 0。因此,公式(3)中的
可改写为
, (4)
, (5)
, (6)
, (7)
, (8)
其中
是z = 10 m时的湍流强度;
是背景成分因子;R是共振分量因子;
和
为拟合系数;
和
分别为脉动风荷载的垂直方向和水平方向相关系数;
是局部轮廓宽度;
是一阶模态的阻尼比;
是一阶模态频率值。
但该类输电塔在现实中很少见。一般输电塔的塔身成锥形。均匀锥形输电塔的
和
随高度变化,可通过锥度变化进行近似。为分析更为现实输电塔的风振系数计算模型,在此不考虑横担和法兰盘的影响。为了避免混淆,上标“*”被添加到
等,表示结构的形状随高度而变化,如
等。
, (9)
, (10)
, (11)
其中
是局部湍流强度;
是考虑整体形状变化的
修正系数;
是考虑局部形状变化的
的校正系数。
通过公式(6)计算
时,
。将公式(9)代入公式(4),可以获得均匀锥形输电塔的
。
与主塔身不同,横担的质量和挡风面积随高度局部突变。在此讨论横担的质量和挡风面积的变化规律,建立了输电塔风振系数的现实计算模型。
如图2所示,横担的宽度大于主塔身的宽度,引入了
的修正系数
:
(12)
其中
和
分别是水平相关函数和垂直相关函数。
主要受输电塔外形的影响,计算模型可简化为图3。
为主塔身宽度;
为每个横担的单个横向平均宽度;
为塔身附近每个横担的厚度相同且平均值;
为两个相邻横担之间的中心距离平均值。通过分析,
主要受横担宽度和数量的影响。此外,每个横担宽度的差异对于塔架来说并不显著,因此图3的简化计算模型无误。

Figure 3. Simplified calculation model of
图3.
的简化计算模型
根据上述分析,
的影响参数为
,
,
,
,h和nc,其中nc是横担的数量。根据塔结构的控制关系,
随h增加;
随
增加。由电气要求控制,
、
与电压水平相关,与结构要求无关。同样,nc也受电气要求控制。法兰盘的形状分布受主塔身的限制。随着h的增加,法兰盘的挡风面积、质量和
将保持不变。基于上述分析,
的影响参数可简化为
,h和nc。
通过对3座悬臂输电塔的分析(如图4所示),得到表达式为
,
和
。根据塔的有限数量,此处给出的平均数值的标准偏差分别为0.032 (2.291)、0.055 (2.052)和0.314 (5.856)。规定标称高度hn不得小于15 m,可以限制nc值的范围。显然,通过公式计算
很麻烦。为了方便设计,
可查表获取,如表1。

Figure 4. Cantilever transmission tower model
图4. 悬臂输电塔模型

Table 1. α n value of cantilever transmission tower
表1. 悬臂输电塔的
值
需考虑横担质量和挡风面积对
的影响。为此引入了两个校正系数:
(13)
, (14)
其中
是
的附加质量修正系数;
是
的附加挡风面积修正系数;
和
是所有横担和法兰盘的总和符号。
法兰盘布置在主塔身的二分之一处。在确定塔身中法兰盘的布置方式后,需确定挡风面积以及横担和法兰盘的质量。对3个悬臂输电塔(如图4所示)进行了统计分析,以获得以下关系:
,
,
和
。此处给出的平均数值的标准偏差分别为0.012 (4.576)、0.061 (2.071)、0.034 (3.325)和0.057 (2.676)。
本文确定的横担和法兰盘的M和As的简化分布不仅建立了与主塔身的关系,而且采用了图3中的计算模型。这些分布达到了简化计算的目的。因为
和
的独立影响参数是
,h,nc和
,为了方便制表,设
。
将
、
、
和
代入公式(13)和(14),可计算
。同样,在工程设计参数范围内,为便于计算,将
制成表格,如表2所示。在表2中,令
,列出了与T = 0.3和T = 0.5相对应的
。

Table 2. α y value of cantilever transmission tower
表2. 悬臂输电塔的
值
主塔身的
、横担的
和法兰盘的
可用以下公式计算:
, (15)
, (16)
, (17)
, (18)
当计算悬臂输电塔的
时,
将修正系数
和
添加到公式(9)中。为了确保表达式的简单性和与中国荷载规范(GB 50009-2012, 2012)中的
表达式的一致性,将主塔身和横担的
合并为一个
公式(公式(19))。横担是离散分布的,因此可以分段计算,每个分段的计算高度作为其几何中心的高度。由局部形状变化引起的校正系数
分别根据公式(15)至(17)计算。
, (19)
将公式(19)代入公式(4),可以获得带有悬臂的输电塔的
值。
3. 影响参数分析
本节讨论了横担和法兰盘对悬臂输电塔的
和
的影响,并对影响参数进行计算和分析。
为此设置了三种工况。用于图2中1号塔分析这三种工况。工况1仅考虑主塔身;工况2在工况1的基础上增加法兰盘;工况3在工况2的基础上增加横臂。本文涉及的计算是对悬臂输电塔进行有限元分析,本文有限元建模方法与参考文献 [5] 中的一致,该建模方法的准确性在文献 [5] 中得到了充分验证,能够保证计算结果的准确性。
如图5所示,计算了三种工况下输电塔的
和
值。如图5(a)所示,图5(a)中主塔身的工况1和工况2以及图5(b)中主塔身的工况2和工况3的R.M.S.差异分别为0.024和0.135。因此,主塔身的
随考虑法兰盘的影响而下降,但主塔身和法兰盘的
考虑横臂的影响而下降。
受法兰盘影响小,受横担影响大。因此,在计算
时不可忽略横担的因素,现行规范中未考虑横担的影响,本文提出的方法相较规范更为准确。同时使用本文的方法计算
时大约2秒,而有限元计算约3小时10分钟,因此使用本文提出的方法相较有限元计算更便捷。如图5(b)所示,主塔身的
随考虑法兰盘的影响而增加,但主塔身和法兰盘的
考虑横臂的影响而增加。横臂和法兰盘对
和
的影响相反的。由于横臂的挡风面积和质量较大,且位于输电塔的上部,横臂对输电塔的
和
的影响很明显。

(a)
(b)
Figure 5.
and
values of cantilever transmission tower based on inertial force method
图5. 基于惯性力法悬臂输电塔的
和
值
4. 结论
●为了分析法兰盘和横担的影响,设置了三种工况,并计算了三种工况下输电塔的
和
值。经过分析,对于输电塔而言,
受法兰盘影响小,受横担影响大;而
受法兰盘影响大,受横担影响小。因此,作为近似计算,法兰盘对风振系数的影响可以忽略不计。
●悬臂输电塔三部分的
随高度增加而增加。对于给定高度,法兰盘的
最大,但对整体风振系数贡献小;横担的
最小,但对整体风振系数贡献大。通过时域分析得到的输电塔的
与风振系数计算结果吻合良好,表明本文提出的风振系数公式符合工程要求。
●本文基于惯性力法,提出了输电塔风振系数实用计算方法,该方法与现有规范中计算方法相比计算更为准确,与ANSYS有限元计算对比计算速度更快。但输电塔的类型很多,本文仅确定了悬臂输电塔的风振系数表达式,其他类型的输电塔需酌情考虑。
基金项目
本研究项目由重庆科技学院校企协同创新中心开放研究项目资助,批准号为YKJCX2220624。