1. 引言
我国秸秆总量达到了世界秸秆总产量的20%~30%。目前,秸杆的回收再利用主要方式包括秸秆还田、制备生物质能源、制备饲料等 [1] [2] [3] [4] [5]。但秸秆的综合利用率仍然较低,每年都有大量的秸秆被作为农作物废弃物或直接就地焚烧,导致了严重的生物质资源浪费和环境污染等问题 [6]。另一方面,建筑资源短缺严重制约经济社会发展,传统建材已导致社会资源的巨大消耗和生态的严重破坏。众所周知,以秸秆作为建筑工程的原材料制备墙体,具有隔热、隔声、质量轻、强度高、节约成本等优点,可以减少取暖总热耗和取暖总成本,满足“可持续性”建筑墙体材料所具备的各种条件 [7]。因此,积极推进秸秆的建材化利用,可以有效解决木材供需矛盾和农业秸秆浪费、焚烧带来的问题,是将碳永久固定在建筑物之中是实现碳达峰、碳中和的有效路径。众多学者对含有秸秆的建筑材料做了大量的研究工作。
刘巧玲 [8] 、吕信敏 [9] 、曾哲 [10] 、Wang等人 [11] 均研究了秸秆掺量对所制复合墙体材料力学性能的影响,研究结果表明:秸秆掺量的增加可提高复合材料的力学性能。M. Kozlowski、M. Kadela等人 [12] 研究秸秆纤维、粉煤灰的掺量对于复合泡沫混凝土的密度、收缩率以及强度的影响,并通过试验给出最佳配和比。刘保华 [13] 、肖力光等人 [14] 利用油菜秸秆灰分与稻草秸秆纤维制备混凝土,研究植物纤维复合混凝土的保温性能,研究结果表明:添加一定量的植物纤维混凝土导热系数低于基体混凝土,并且随着纤维掺量的增大,导热系数呈下降趋势,保温性能更好。Costes J.P. [15] 、Conti L. [16] 、Marques B.等人 [17] [18] [19] 研究了秸秆包的热导系数与密度的关系,其中最小导热系数为0.039 w/(m∙k)。
目前,对于秸秆复合墙体材料性能的研究多集中在材料的自身参数上,在成型工艺方面的研究较少。针对此问题,本项目采用响应面分析法探索秸秆墙板压缩成型过程中最佳的工艺参数组合,可促进秸秆的建材化利用,为未来相关研究提供参考。
2. 材料与方法
2.1. 试验材料
1) 小麦秸秆
本论文试验所用稻草秸秆均由江苏省盐城市建湖县龙达秸秆专业合作社提供,株高为50至80 cm。
2) 胶凝材料
胶凝材料采用本课题组研制开发的无机硅铝胶凝材料。
2.2. 试验设备
试验设备包括:压缩模具(自制);E602型电子天平(上海浦春计量仪器有限公司);WDW-50C型电子万能材料试验机(上海华龙测试仪器有限公司);JXMEA-6000型数显电热鼓风干燥箱(余姚市亚泰仪表有限公司);水泥砂浆搅拌机(无锡建材试验仪器机械厂)。
2.3. 试验方法
2.3.1. 样本的制备
利用斩刀将收割的小麦秸秆切成长度为5 cm左右的秸秆段,通过干燥箱烘干处理后,测定其含水率为8%,以麦秸秆物料与胶凝材料以质量比为3:7的比例放入搅拌锅中搅拌五分钟后样本制备完成。
2.3.2. 制板拌合物压缩试验
每次试验时,为避免样本排列方法以及均匀程度对试验造成影响,将样本随机杂乱且均匀的填充到压缩模具中,直至填满,为防止物料与压头发生粘黏,在物料填充结束后,铺设一层吸油纸。设定电子万能试验机的试验程序,将系统清零后开始压缩试验。同种因素水平试验重复3次,结果取平均值。
2.3.3. 试验指标
秸秆墙板的密度可直接影响墙板的综合性能,密度越大其力学性能越优。残余力能够反映压缩工艺完成后墙板的稳定性。比能耗是直接反映设备功耗的一项重要参数,功耗越大生产秸秆墙板所需的费用越高。因此,本研究以墙板成型密度、残余力、比能耗作为评价工艺性能的指标。指标的测试方法如下:
1) 密度
压缩完成后读取万能试验机上的位移,通过式(1)计算可得到密度。
(1)
式(1)中:ρ为密度,kg/m3;m为物料重量,kg;S为压缩装置底面积,m2;L0为压缩装置深度,m;L为万能试验机压头位移,m。
2) 残余力
通过调整万能试验机的运行程序,使其达到相应的压力后保持压头位移不变,30分钟后压头所受的反向压力即为墙板内部残余力,可直接读取。
3) 比能耗
比能耗为在压缩单位质量的物料过程中设备所需要消耗的能量。其计算公式为:
(2)
式(2)中:δ为比能耗,J/kg;W为压缩过程的总能耗,J;m为物料重量,kg;F(x)为压缩过程随位移变化的载荷,N。
2.3.4. 单因素试验
单因素试验设定三因素分别为压力、喂入量、压缩速度。考察三因素对试验指标的影响。先固定喂入量为300 g,压缩速度为100 mm/min,压力分别为0.1 MPa,0.4 MPa,0.7 MPa,1.0 MPa,1.3 MPa;然后固定压力0.7 MPa,压缩速度为100 mm/min,喂入量分别为225 g,300 g,375 g,450 g,525 g;最后固定压力0.7 MPa,喂入量为300 g,压缩速度分别为50 mm/min,100 mm/min,150 mm/min,200 mm/min,250 mm/min。
2.3.5. 响应面设计
以单因素实验为前提,根据Box-Behnken Design试验的设计原理,选取压力,喂入量,压缩速度三因素作为试验的自变量,密度,残余力,比能耗作为响应值。试验因素与水平的取值如表1。
3. 结果与分析
3.1. 单因素试验结果
3.1.1. 压力对试验指标的影响
由图1可知,当喂入量为300 g,压缩速度为100 mm/min,压力分别为0.1 MPa,0.4 MPa,0.7 MPa,1.0 MPa,1.3 MPa时,随着压力的增加,密度不断增加,在压力达到0.7 MPa后,增势变缓。这是由于物料在压力作用下由“松散阶段”逐渐进入到“压紧阶段”,其自身体积模量随密度的增加而增加,使其自身密度的增长速度随压力的增加逐渐变慢。随着压力的增加,设备的比能耗也在增加,比能耗的影响因素主要有设备提供的压力,压头在压力方向的位移和被压缩物料的质量,由图1可知被压缩物料的质量一定,压力增加,物料被压缩的程度增大,压头位移增大,所以设备的比能耗增加。残余力随着压力的增加也呈上涨趋势,这是因为物料所受的外界压力越大,其所需的应力松弛时间越长,因此当保压时间相同时,压力越大,残余力越大。在压缩后期压力对总体指标的影响程度较小,因此,取压力的水平范围为0.1 MPa~0.7 MPa。
3.1.2. 喂入量对实验指标的影响
由图2可知,当压力为0.7 MPa,压缩速度为100 mm/min,喂入量分别为225 g,300 g,375 g,450 g,525 g时,随着喂入量的增大,墙板的成型密度逐渐减小,这是由于物料的松散程度取决于物料的初始密度,即喂入量的大小,喂入量增大,物料的松散程度降低,对物料施加同样的力,大喂入量的物料的变形量更小,其成型密度也就越小;随着喂入量的增大设备的比能耗呈下降趋势,原因是在压头提供相同压力的情况下,随着喂入量的增大,物料质量增大,压头的位移减小,使比能耗下降;随着喂入量的增大,残余力逐渐减小,这是由于喂入量增大,墙板成型后密度较小,相对与小喂入量的成型墙板略微松散,因此其内部的初始残余力相对较小。根据试验结果,秸秆胶凝材料的的应力松弛率基本一致(33%左右),可以得出,成型后内部初始残余力较小的秸秆墙板在保压相同时间内其最终残余力也较小。在喂入量达到375 g后对总体指标的影响程度较小,因此,取喂入量的水平范围为225 g~375 g。
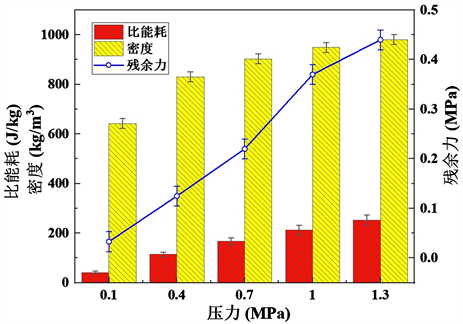
Figure 1. Effect of pressure on test indicators
图1. 压力对试验指标的影响
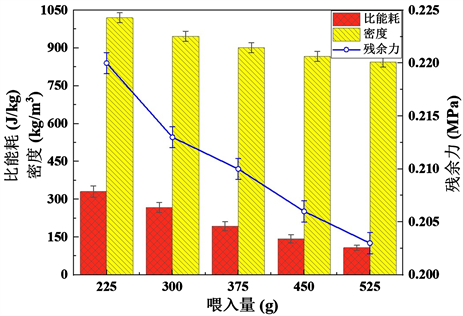
Figure 2. Effect of feeding amount on test indicators
图2. 喂入量对试验指标的影响
3.1.3. 压缩速度对试验指标的影响
由图3可知,当压力为0.7 MPa,喂入量为300 g,压缩速度分别为50 mm/min,100 mm/min,150 mm/min,200 mm/min,250 mm/min时,随着压缩速度的增加,墙板成型的密度减小。从农业物料流变学角度分析,呈现这种规律的原因是,秸秆自身的黏弹属性在其压缩过程中既有弹性变形,又有粘性变形,且流变学行为受到物料状态的影响。在弹性变形相同的情况下,随着压缩速度的增大,剪切应力造成的物料粘性流动逐渐增大,需要更大的压缩力来抵消物料被压缩产生的弹性变形和粘性变形。因此,压缩速度增大时,此时物料的可压缩性变差,物料的密度减小。随着压缩速度的增大,比能耗降低,这是由于压缩速度增大,物料的变形量减小,压头整体做功减少,因此比能耗降低。随着压缩速度的增大,残余力也呈降低趋势,这是由于成型密度越大,初始残余应力越大,经过相同时间的衰减,最终的残余应力也越大。在压缩速度达到150 mm/min后对总体指标的影响程度较小,因此,取压缩速度的范围为50 mm/min~150 mm/min。
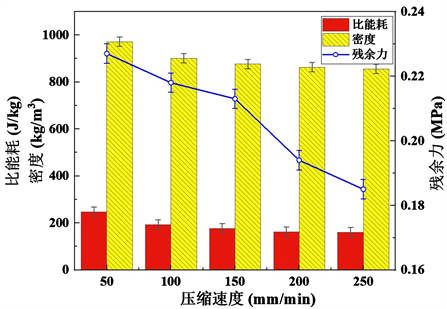
Figure 3. Effect of compression speed on test indicators
图3. 压缩速度对试验指标的影响
3.2. 响应面分析法优化试验结果及分析
根据Box-Behnken的设计原理,设计三因素三水平总共17个试验点的响应面分析试验结果如表2。

Table 2. Response surface experimental design and results
表2. 响应面试验设计及结果
3.2.1. 密度回归模型与方差分析
由试验结果可知,密度ρ的回归模型更符合二次非线性回归方程,通过Design Expert数据分析软件中试验结果与二次非线性回归方程的拟合可得到密度ρ回归模型中的各项参数以及模型的方差分析,如式(3)和表3所示:
(3)
式(3)中:A为压力,MPa;B为喂入量,g;C为压缩速度,mm/min。

Table 3. Analysis of variance for density regression models
表3. 密度回归模型的方差分析
注:P < 0.01为极显著,P < 0.05为显著。
由表3分析可知,模型中A、B、C的P值均小于0.0001,可知压力、喂入量和压缩速度对秸秆墙板压缩成型后密度的影响极为显著,AB、AC、BC的P值均小于0.05,可知各因素的交互作用对秸秆墙板压缩成型后密度的影响显著,失拟项的P值大于0.05,可知失拟项对指标的影响不显著。通过比较模型中A、B、C的F值可知各因素对密度影响的主次顺序为压力 > 喂入量 > 压缩速度。
此模型拟合决定系数达到0.9899,调整后也达到0.9768,变异系数仅为2.18%,说明此模型与试验结果的拟合程度很高。由图4可知,预测值与实测值基本一致,说明试验误差小,此模型可用于预测秸秆墙板压缩成型密度的变化情况。
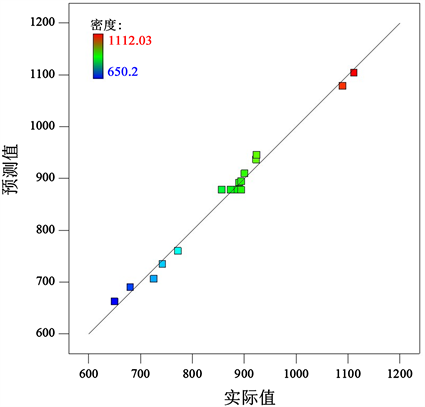
Figure 4. Relationship curve between actual density value and predicted value under experimental conditions
图4. 试验条件下密度实际值与预测值关系曲线
根据回归方程作出响应面分析图,见图5~图7。

Figure 5. Effect of pressure and feed volume interaction on density
图5. 压力与喂入量交互作用对密度的影响

Figure 6. Effect of pressure and compression speed interaction on density
图6. 压力与压缩速度交互作用对密度的影响
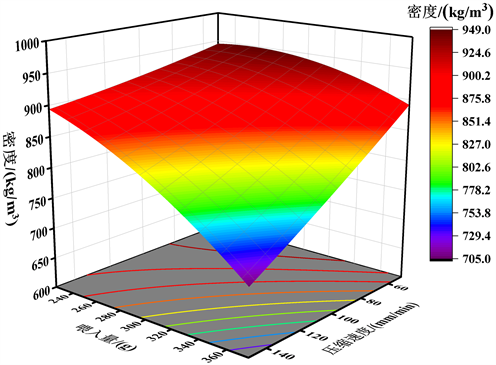
Figure 7. Effect of feed amount and compression speed interaction on density
图7. 喂入量与压缩速度交互作用对密度的影响
从图5~图7中可以看出,在所选的范围内回归模型存在最大值。喂入量和压缩速度交互作用立体图曲线最陡峭,这说明两者的交互作用效应最为显著。压力和喂入量交互作用立体图曲线相对平缓,说明交互作用相对较差。压力与压缩速度交互作用立体图曲线最平缓,说明两者交互作用最不明显。
3.2.2. 比能耗回归模型与方差分析
由试验结果可知,比能耗δ的回归模型也符合二次非线性回归方程,通过Design Expert数据分析软件中试验结果与二次非线性回归方程的拟合可得到比能耗δ回归模型中的各项参数以及模型的方差分析,如式(4)和表4所示:
(4)

Table 4. Analysis of variance compared to energy regression model
表4.比能耗回归模型的方差分析
注:P < 0.01为极显著,P < 0.05为显著。
由表4分析可知,模型中A、B、C的P值均小于0.0001,可知压力、喂入量和压缩速度对压缩工艺结束后设备比能耗的影响极为显著,AB、AC、BC的P值均小于0.05,可知各因素的交互作用对压缩工艺结束后设备比能耗的影响显著,失拟项的P值大于0.05,可知失拟项对指标的影响不显著。通过比较模型中A、B、C的F值可知各因素对比能耗影响的主次顺序为压力 > 喂入量 > 压缩速度。
此模型的拟合决定系数达到0.9955,调整后也达到0.9897,变异系数仅为3.88%,说明此模型与试验结果拟合程度很高。由图8可知,预测值与实测值基本一致,说明试验误差小,此模型可用于预测设备完成压缩工艺时比能耗的变化情况。
根据回归方程作出响应面分析图,见图8~图10。
从图9~图11中可以看出,在所选的范围内回归模型也存在最大值。喂入量和压缩速度交互作用立体图曲线最陡峭,这说明两者的交互作用效应最为显著。压力和喂入量交互作用立体图曲线陡峭,说明交互作用明显。压力与压缩速度交互作用立体图曲线最平缓,说明两者交互作用最不明显。
3.2.3. 残余力回归模型与方差分析
由试验结果可知,残余力F的回归模型更符合线性回归方程,通过Design Expert数据分析软件中试验结果与线性回归方程的拟合可得到残余力F回归模型中的各项参数以及模型的方差分析,如式(5)和表5所示:
(5)
由表5分析可知,模型中A、C的P值均小于0.0001,可知压力和压缩速度对秸秆墙板压缩成型后内部残余力的影响极为显著,B的P值小于0.05,可知喂入量对秸秆墙板压缩成型后内部残余力的影响显著。由于本模型为线性回归模型因此不涉及各因素交互对试验指标的影响。失拟项的P值大于0.05,可知失拟项对指标的影响不显著。通过比较模型中A、B、C的F值可知各因素对密度影响的主次顺序为压力 > 压缩速度 > 喂入量。
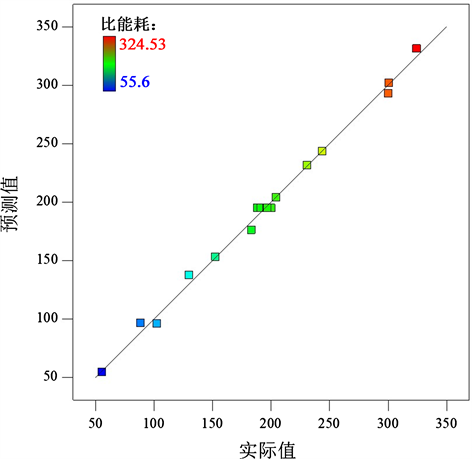
Figure 8. Relationship curve between actual value and predicted value of specific energy consumption under test conditions
图8. 试验条件下比能耗实际值与预测值关系曲线

Figure 9. Pressure and feed volume interaction compared to the effect of energy consumption
图9. 压力与喂入量交互作用对比能耗的影响

Figure 10. Pressure and compression speed interaction compared to the effect of energy consumption
图10. 压力与压缩速度交互作用对比能耗的影响
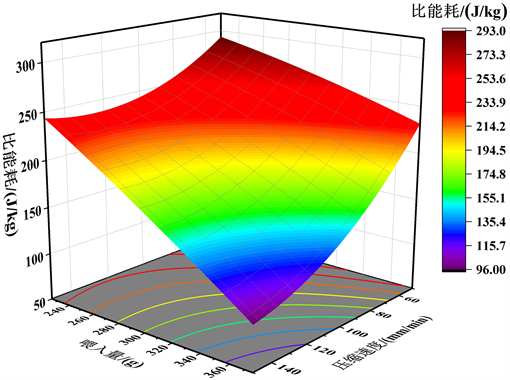
Figure 11. Interaction between feed volume and compression speed compared to the effect of energy consumption
图11. 喂入量与压缩速度交互作用对比能耗的影响

Table 5. Analysis of variance for residual force regression model
表5. 残余力回归模型的方差分析
注:P < 0.01为极显著,P < 0.05为显著。
此模型拟合决定系数达到0.9961,调整后也达到0.9925,变异系数仅为3.56%,说明此模型与试验结果的拟合程度很高。由图12可知,预测值与实测值基本一致,说明试验误差小,此模型可用于预测秸秆墙板压缩成型后内部残余力的变化情况。
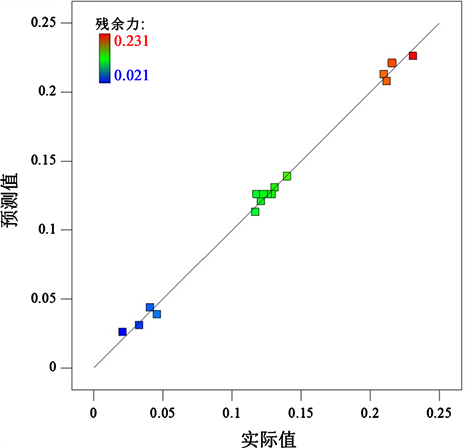
Figure 12. Relationship curve between actual and predicted residual force under test conditions
图12. 试验条件下残余力实际值与预测值关系曲线
3.3. 优化工艺参数及试验验证
3.3.1. 参数优化
利用Design Expert软件对工艺参数进行优化,取密度的优化目标为最大,比能耗和残余力的优化目标为最小,设置约束条件,如表6。
根据表4.7设定的优化目标进行优化,获得秸秆墙板压缩过程的最佳工艺参数为:压力为0.47 MPa,喂入量为280.98 g,压缩速度为91.42 mm/min,其密度为934.60 kg/m3,比能耗为231.30 J/kg,残余力为0.15 MPa。
3.3.2. 试验验证
为验证优化结果的合理性与可靠性,本文在上述最优的试验因素组合下进行验证试验,验证结果如下:密度为891.63 kg/m3,比能耗为201.4 J/kg,残余力为0.134 MPa,各评价指标误差均在15%以内,说明优化结果具有较高的可信度,同时,证明本试验得到的研究模型是可靠的,可用于实际生产过程中各参数的选取。

Table 6. Optimizing constraint settings
表6. 优化约束条件设置
4. 结论
本文主要通过单因素试验结合响应面分析法对秸秆墙板成型过程中的工艺参数进行优化,具体结论如下:
1) 通过单因素试验中,以墙板的成型密度、设备比能耗和残余力为指标,探讨压力、喂入量、压缩速度对墙板成型工艺的影响,并试验结果表明,各试验指标随着压力的增大而增大,随着喂入量的增大而减小,随着压缩速度的增大而减小。
2) 根据单因素试验结果,进行响应面分析得到了影响因素与试验指标的回归数学模型以及各因素对试验指标的影响显著性。结果表明,各因素对密度影响的主次顺序为压力 > 喂入量 > 压缩速度,对比能耗影响的主次顺序为压力 > 喂入量 > 压缩速度,对残余力的影响主次顺序为压力 > 压缩速度 > 喂入量。
3) 通过参数优化确定最佳的参数组合为:压力为0.47 MPa,喂入量为280.98 g,压缩速度为91.42 mm/min。其密度为891.60 kg/m3,比能耗为231.30 J/kg,残余力为0.15 MPa。通过验证试验表明,得到的数学模型对于本文所选试验范围是合理可靠的。
NOTES
*通讯作者。