1. 引言
《数学分析》是各大高校数学专业的必修基础课,它不仅是数学各分支的基础,还是后续专业知识的奠基石,基础不牢,地动山摇。著名数学家华罗庚先生曾说:新的数学方法和概念,常常比解决数学问题本身更重要。而概念本身就蕴含着丰富的数学思想和方法,比如极限思想、积分思想等。并且概念的产生过程也蕴含着科学家从事科学研究的一般方法,这些对学生思维观、方法论的形成至关重要。
2020年5月,教育部党组会议审议通过《高等学校课程思政建设指导纲要》 [1] ,《纲要》指出理学类课程要注重科学思维方法的训练和科学伦理的教育。但数学概念具有高度的抽象性、严密的逻辑性,那么如何将科学思维方法与抽象的概念 [2] [3] ,有机融合并春风化雨般渗透到教学实践中呢?本文以“定积分”和“对坐标的曲面积分”的教学设计为例阐述数学概念中蕴含的科学思维方法。
2. 定积分概念的教学设计
定积分 [2] [3] [4] [5] 是从实际问题中抽象出来的数学概念,是数学分析教学中的一个重要知识模块。它是学习微积分的基础知识,也是后续教学内容(定积分的应用、重积分、曲线积分、曲面积分)的必备知识,更是解决许多实际问题的工具。定积分理论的建立对于数学的发展产生了深远的影响。
2.1. 教学目标
1) 知识与技能:了解定积分的背景;理解定积分的概念、几何意义、物理意义;体会定积分的本质思想,会用定义计算简单的定积分。
2) 过程与方法:通过分析不同背景问题中蕴含的相同数学内涵,培养学生分析、探究、归纳得出数学概念和规律的学习能力,提高从数学角度分析和看待问题的能力。
3) 情感与价值观:第一:通过对不同背景下的问题用相同的数学方法进行揭示,认识数学与实际生活的联系。第二:探讨定义中所体现的数学思想,一是近似的思想,体现为以直线代替曲线,以规则代替不规则;二是极限的思想,体现为由近似值得到精确值时,需取极限;三是积分思想,主要解决不均匀型问题;进而折射出人生哲理,不积跬步,无以至千里;不积小流,无以成江海。
2.2. 教学内容、重点以及重难点的处理方法
1) 教学内容:定积分的概念和意义、可积性、定积分存在的充分条件、必要条件。
2) 教学重点:利用“分割、近似代替、求和、取极限”四个步骤,归纳出定积分的概念。
3) 教学难点:定积分概念、“无限逼近”思想的形成过程及理解。
4) 教学重难点的处理方法:通过问题引入,激发学生的学习兴趣。在问题探究中,结合PPT动画展示“小矩形面积和”无限接近“曲边梯形面积”的过程,化抽象理解为直观演示。然后从研究方法、技术路线、结构形式上对结果分析,抽象概括出定积分的概念(如图1)。
2.3. 教学过程
2.3.1. 问题引入
介绍当今世界上面积前十国家(播放视频),每个国家的陆地边界,形状迥异,有的迂回曲折,有的犬牙交错。随之将话题转到各个国家的陆地面积是如何计算出来的呢?将知识迁移到实际问题中,使学生感受到数学知识来源于生活服务于生活,激发学生学习的积极性。
2.3.2. 问题探究
各个国家的陆地面积的计算问题,就抽象为数学问题:如何求平面封闭曲线所围成的图形的面积。对于这样一个不规则的平面图形,它的面积是无法直接求解的,如何处理呢?
问题简化:对问题简化是研究问题的第一步,这亦是一般性的科学研究方法。
分析:对图形分割,那么要求这个不规则图形的面积就转化为求曲边梯形的面积(问题的本质)。
引例1已知曲边梯形是由连续曲线
及
轴、直线
,
所围成,求其面积A。
分析类比与求解问题关联最紧密的简单情形。
1) 若
(常数),则面积
。
2) 若闭区间
的长度很小,则
可近似看作常数,转化为情形1)。
3) 对一般的闭区间
,如何求解呢?
根据1)和2),可用矩形面积近似代替曲边梯形面积。直观上:小矩形的个数越多,其面积之和越接近曲边梯形的面积。
引导学生思考:如果无限细分下去,所得小矩形的面积之和的极限即为曲边梯形面积的精确值。
通过“分割、近似代替、求和、取极限”可求得曲边梯形的面积
。
提问通过取极限,当无限细分时,实现从近似过渡到精确。那如何刻画无限细分?能否用
刻画呢?
注1引导学生体会用有限来研究无限的哲学思想。
引例2已知某物体作直线运动,速度
,且
,求在运动时间内物体经过的路程s。
引例1与引例2完全类似,利用“分割、近似代替、求和、取极限”的思想,求得物体所经过的路程
。
2.3.3. 概念形成
详细的定积分概念不再陈述 [6] 。此时回看引例1和引例2。可知曲边梯形的面积
,其

Figure 1. The process of exploring the concept of definite integral
图1. 定积分概念的探究过程
中
,变速直线运动的路程
,其中
。它们分别从几何角度和物理角度阐述了定积分的意义。引导学生思考如下问题:
1) 若
,则
与曲边梯形的面积有何关系呢?
2) 对任意的
,
表示什么意思?
在此教学环节中,还要启发学生思考定积分存在的充分条件和必要条件。类比函数在一点处极限的定义,引导学生给出定积分
定义的“
”表述。
2.3.4. 巩固新知
例1 讨论下列函数在
上的可积性。
1)
;
2)
。
例2求下列平面图形的面积。
1) 计算由
,
及x轴所围成图形的面积A。
2) 计算由
,
,
及x轴所围成图形的面积A。
例3用定积分表示下列极限。
1)
;
2)
。
注2例3 考察学生逆向思维能力。定积分的本质是一类乘积的和式的极限,那么给定一个乘积的和式的极限,如何将其表示为定积分呢?
思考例3的1)中,若将
,那么
的定积分表达式又是什么形式呢?
2.3.5. 总结思考
如图2中的定积分概念的教学设计可做如下思考:
思考与练习
1、定积分主要解决实际中的哪类问题?
2、函数
在
上可积的充分条件?
3、用定积分表示极限:
。
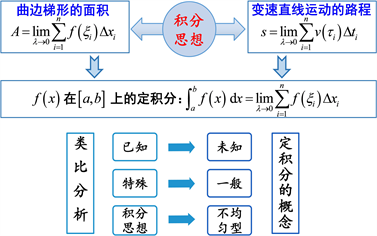
Figure 2. Teaching design of the concept of definite integral
图2. 定积分概念的教学设计
3. 对坐标的曲面积分概念的教学设计
对坐标的曲面积分 [7] 是关于在坐标面投影的曲面积分,它是多元函数微积分学的重要组成部分之一,其与重积分、曲线积分、对面积的曲面积分都有联系。
3.1. 教学目标
1) 知识与技能:掌握对坐标的曲面积分概念、性质及其计算方法和步骤。了解利用数学知识解决实际问题的一般过程,提高应用数学知识的意识。
2) 过程与方法:能够将实际问题转化为一个数学问题,通过分析问题,建立不同变量对应的函数关系,求解对坐标的曲面积分,培养学生分析问题、转化问题和解决问题的数学思维和求解能力。
3) 情感与价值观:利用积分思想解决不均匀型问题,让学生体会黎曼积分的辩证统一,加强思政教育;积分思想折射出人生哲理,在奋斗的路上脚踏实地完成一个个小目标,不断追求,总有一天个人梦及中国梦都会实现。
3.2. 教学内容、重点以及重难点的处理方法
1) 教学内容:了解对坐标的曲面积分的物理背景;理解对坐标的曲面积分的概念、性质、计算方法及两类曲面积分之间的联系。
2) 教学重点:对坐标的曲面积分的计算。
3) 教学难点:对坐标的曲面积分的概念的理解、两类曲面积分之间的联系。
4) 教学重难点的处理方法:通过创设情境(三峡大坝泄洪),引入问题,在问题探究中,从研究过程、技术路线、结构形式上分析流量问题,引导学生抽象概括对坐标的曲面积分的定义(如图3)。然后借助典型例题展示对坐标的曲面积分的计算,让学生仿照类比,内化于心,掌握其计算方法。
3.3. 教学过程
3.3.1. 问题引入
介绍当今世界上最大的水利发电工程——我国的三峡大坝,随之将话题转到三峡大坝的泄洪作用上,如何计算单位时间内从坝的一侧流向另一侧的河水流量呢?(以视频形式播放)。
3.3.2. 问题探究
引导学生思考:计算流量需要考虑哪些因素?
按照科学研究的一般方法:从简单到复杂、从特殊到一般,从具体到抽象。为方便分析问题和建立数学模型,作以下假设。
假设 不可压缩的流体通过同一个流管作定常流动时,每一时刻流管的各截面流量相同。此时可将上述问题抽象为数学模型。
模型 设流体不可压缩,密度
,流体的速度
,
坝体所在的定向曲面为
,函数P,Q,R在所讨论范围上连续,求单位时间内流体流过曲面
指定侧的流量
。为简化符号,将速度v的三个分量分别记为P,Q,R。
分析 对于这种不均匀型问题,引导学生利用“分割–近似代替–求和–取极限”的积分思想和方法解决问题。
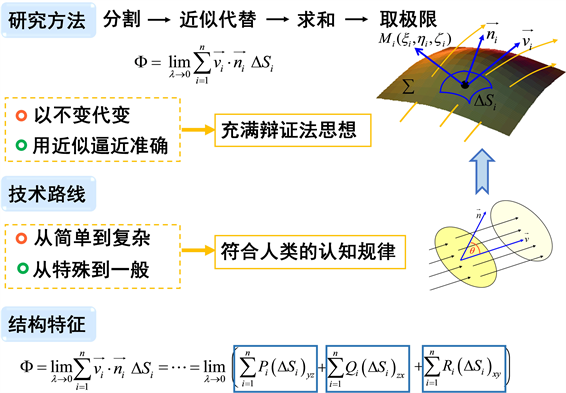
Figure 3. The process of exploring the concept of curved surface integral of coordinate
图3. 对坐标的曲面积分概念的探究过程
3.3.3. 概念形成
详细的对坐标的曲面积分的概念 [8] 不再陈述。在这个教学环节中,还要启发学生思考对坐标的曲面积分的性质和计算方法(略)。
3.3.4. 巩固新知
例4计算
,其中
是平面
与三个坐标面所围成的几何体的表面,方向取外侧。
例 5计算
,其中
是圆柱面
,方向取外侧。
思考计算
,其中
是圆柱体
的整个表面,方向取外侧。
注3对比例5,注意二者的区别与联系。
3.3.5. 总结思考
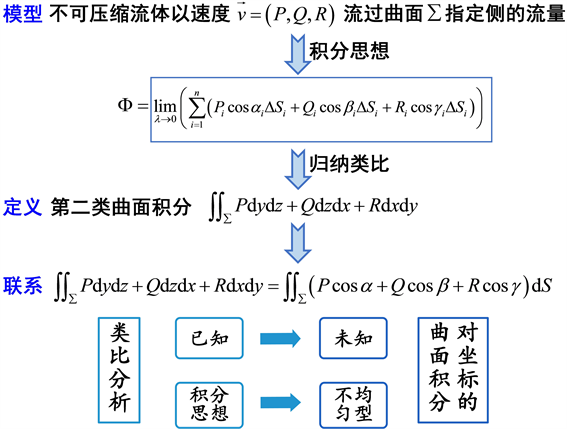
Figure 4. Teaching design of the concept of curved surface integral of coordinate
图4. 对坐标的曲面积分概念的教学设计
如图4中的定积分概念的教学设计可做如下思考:
思考与练习
1、两类曲面积分之间的联系
其中
是
指定侧的单位法向量。在两类曲面积分的定义中,一个与曲面的侧有关,一个与曲面的侧无关,上述关系式矛盾吗?
2、计算曲面积分
,其中
是抛物面
介于
与
之间的部分,方向取下侧。
3、计算曲面积分
,其中
是锥面
,方向取外侧。
4. 结束语
定积分和对坐标的曲面积分是两个不同的概念,它们都蕴含了积分思想(处理不均型问题),从横向分析的角度看,这二者之间既有联系也有区别。在概念的形成过程中,二者的研究方法(“分割、近似代替、求和、取极限”)、技术路线设计(从简单到复杂,从特殊到一般)是完全类似的;从结构形式上看,二者都是一类有限不定和式的极限,但对坐标的曲面积分是与曲面的侧有关的有限不定和式的极限。
在上述两个概念的教学设计中——问题探究环节,利用已知研究未知,借助积分思想解决不均匀型问题,分析问题特征,化归已知方法,抽象概括出数学概念。这种认识问题、分析问题、解决问题的一个过程,有助于训练学生的科学思维方法,进而培养学生探索未知世界的责任感和使命感。
参考文献