多边形永磁体磁场的数值分析

期刊菜单

多边形永磁体磁场的数值分析
Numerical Analysis of Magnetic Field of Polygonal Permanent Magnet

DOI:10.12677/PM.2023.131006,PDF,HTML,XML,下载: 366浏览: 599
作者:宋涛,何志琴^*：贵州大学电气工程学院，贵州贵阳
关键词:多边形永磁体；六边形永磁体；八边形永磁体；磁通量密度；数值分析；有限元分析；Polygonal Permanent Magnet；Hexagonal Permanent Magnet；Octagonal Permanent Magnet；Magnetic Flux Density；Numerical Analysis；Finite Element Analysis

摘要:永磁体的磁场分布是其工程应用的基础。本文以六边形永磁体和八边形永磁体为例，应用等效面电流法对多边形永磁体的磁场分布进行数值分析，经有限元仿真结果验证了数值表达式的正确性。分析了八边形永磁体较相应尺寸的矩形永磁体的磁场分布优势。

Abstract:The magnetic field distribution of permanent magnet is the basis of its engineering application. In this paper, taking hexagon permanent magnet and octagon permanent magnet as examples, the equivalent surface current method is used to analyze the magnetic field distribution of polygon permanent magnet. The finite element simulation results verify the correctness of the numerical expression. The advantages of magnetic field distribution of octagonal permanent magnet com-pared with rectangular permanent magnet of corresponding size are analyzed.

文章引用：宋涛, 何志琴. 多边形永磁体磁场的数值分析[J]. 理论数学, 2023, 13(1): 55-66. https://doi.org/10.12677/PM.2023.131006

1. 引言

永磁体的空间磁场分布是其工程应用 [1] [2] [3] [4] [5] 的基础。目前，针对永磁体的磁场分布多采用有限元分析法和数值分析法，后者包括等效面电流法和等效磁荷法。二者均可辅助实现机械结构的设计和优化，但后者可实现机械结构的动力学建模仿真，以降低研制成本。故有必要对多边形永磁体的空间磁场进行数值分析。

矩形永磁体的使用较为广泛 [3] [4] [5]，文 [6] 应用等效磁荷法解析了其磁场分布，文 [7] [8] 应用等效面电流法获得了其磁场分布的解析表达式。文 [9] 基于等效磁荷法研究了梯形永磁体的磁场分布，但其过于简化的推导过程不便于后续研究借鉴，解析式缺乏拓展性。文 [10] 指出，三角形、六边形、八边形等形状的永磁体可能有助于磁机器性能的提升，并基于等效磁荷法，解析了三角形永磁体的空间磁场，但表达式中的参数含义不明，缺乏拓展性。在三维微型数字电磁执行器 [11] [12] [13] [14] [15] 中，六边形永磁体被用作动子，实现了离散位置的控制。文 [12] 将六边形永磁体等效为矩形永磁体来解析其磁场，但因六边形和矩形永磁体结构差异较大，致使二者的磁场分布范围和数值均差异较大，该等效并不合理。磁制冷冰箱中使用八边形阵列的永磁体，提高了其冷却能力 [16]；文 [17] 指出，八边形是磁粉成像技术中最合适的磁铁形状。

但目前还没有六边形永磁体 [15] 和八边形永磁体磁场的解析表达式，不便于实现其工程应用中的动力学建模。故本文以六边形永磁体和八边形永磁体为例，解析了多边形永磁体的磁场分布，并使用有限元分析结果对数值计算结果进行验证。基于解析表达式，分析了八边形永磁体较矩形永磁体的磁场分布优势。

2. 多边形永磁体磁场的解析

2.1. 解析原理

等效面电流法以安培分子环流假说和毕奥–萨伐尔定律为基础。永磁体的面磁化电流J和磁化矢量M之间的关系为

$J = M \times n$ (1)

其中n为磁介质表面单位外法线方向，二者在数值上相等。永磁体的磁化强度M、面磁化电流大小J与其剩余磁通量密度B_r的关系为

$M = J = B_{r} / μ_{0} .$ (2)

其中， $μ_{0}$ 为真空磁导率，取值为 $4 π \times 10^{- 7}$ ，单位为H/m。则薄层电流环dz₀的电流强度I为

$I = J d z_{0} .$ (3)

由毕奥–萨伐尔定律 [18] 的矢量表达式得到线电流元Idl在空间场点P(x,y,z)处产生的磁通量密度为

$d B = \frac{μ_{0}}{4 π} \frac{I d l \times (r - r^{'})}{{| r - r^{'} |}^{3}} .$ (4)

其中，r表示坐标原点到场点P(x,y,z)的矢径； $r^{'}$ 表示坐标原点到源点(x₀,y₀,z₀)的矢径； $r - r^{'}$

表示源点到场点的矢径；且

$d l \times (r - r^{'}) = | \begin{matrix} i & j & k \\ d x_{0} & d y_{0} & d z_{0} \\ x - x_{0} & y - y_{0} & z - z_{0} \end{matrix} |,$ (5)

$| r - r^{'} | = \sqrt{{(x - x_{0})}^{2} + {(y - y_{0})}^{2} + {(z - z_{0})}^{2}} .$ (6)

(4)式在闭合回路及永磁体厚度h上的积分，即为整个永磁体在场点P(x,y,z)处产生的磁通量密度。

2.2. 六边形永磁体

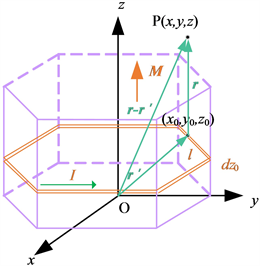
Figure 1. 3D molecular circulation model of hexagonal permanent magnet

图1. 六边形永磁体的三维分子环流模型

Figure 2. 2D analytical model of hexagonal permanent magnet

图2. 六边形永磁体的二维解析模型

六边形永磁体的三维分子环流模型和二维解析模型，分别如图1和图2所示。设图2中斜线的斜率为k，截距为b。x₁、x₂、x₃及y₁、y₂、y₃、y₄分别为各顶点的坐标值。永磁体的边长为amm，高为hmm，其磁化电流密度为J。根据2.1节介绍的永磁体磁场分布的解析原理，以图2中标号为3的载流导体l₃在场点P(x,y,z)处产生的磁通量密度的法向分量 $B_{z_{3}}$ 的计算为例，展开多边形永磁体的磁场分布的解析研究。载流导体3满足(7)式，则由(4)式在闭合回路l及永磁体厚度h上的积分，得到图1所示整个六边形永磁体在场点P(x,y,z)处产生的磁通量密度的法向分量 $B_{z_{3}}$ 为(8)式，进一步化简得到(9)式。

${\begin{cases} y_{0} = k x_{0} + b \\ d z_{0} = 0 \\ d y_{0} = k d x_{0} \end{cases},$ (7)

$B_{z_{3}} = \frac{μ_{0} J}{4 π} \int_{0}^{h} d z_{0} \int_{x_{2}}^{x_{1}} \frac{(y - k x - b) d x_{0}}{{[(1 + k^{2}) {(\frac{x + k y - k b}{1 + k^{2}} - x_{0})}^{2} + {(\frac{k x + b - y}{\sqrt{1 + k^{2}}})}^{2} + {(z - z_{0})}^{2}]}^{\frac{3}{2}}},$ (8)

$\begin{matrix} B_{z_{3}} = \frac{μ_{0} J}{4 π} \int_{0}^{h} \frac{(y - k x - b) d (\frac{x + k y - k b}{1 + k^{2}} - x_{1})}{[{(\frac{k x + b - y}{\sqrt{1 + k^{2}}})}^{2} + {(z - z_{0})}^{2}] {[(1 + k^{2}) {(\frac{x + k y - k b}{1 + k^{2}} - x_{1})}^{2} + {(\frac{k x + b - y}{\sqrt{1 + k^{2}}})}^{2} + {(z - z_{0})}^{2}]}^{\frac{1}{2}}} d (z - z_{0}) \\ - \frac{μ_{0} J}{4 π} \int_{0}^{h} \frac{(y - k x - b) d (\frac{x + k y - k b}{1 + k^{2}} - x_{2})}{[{(\frac{k x + b - y}{\sqrt{1 + k^{2}}})}^{2} + {(z - z_{0})}^{2}] {[(1 + k^{2}) {(\frac{x + k y - k b}{1 + k^{2}} - x_{2})}^{2} + {(\frac{k x + b - y}{\sqrt{1 + k^{2}}})}^{2} + {(z - z_{0})}^{2}]}^{\frac{1}{2}}} d (z - z_{0}) . \end{matrix}$ (9)

式较复杂，按照常规方法难以计算，需先将其化简成文 [19] 中的标准积分形式再计算。在此，定义均以场点坐标分量x、y、z为自变量的函数符号F、F₁、F₂，具体为

$F (x, y, z) = {{\frac{x}{2 | x |} \ln [\frac{| x | - \sqrt{x^{2} + y^{2} + {(z - z_{0})}^{2}}}{| x | + \sqrt{x^{2} + y^{2} + {(z - z_{0})}^{2}}}]} |}_{z_{0} = 0}^{z_{0} = h}$ (10)

$F_{1} (x, y, z) = {\begin{cases} {{\arctan [\frac{x}{y} \frac{z - z_{0}}{\sqrt{x^{2} + y^{2} + {(z - z_{0})}^{2}}}]} |}_{z_{0} = 0}^{z_{0} = h}, (y \neq 0) \\ 0, (y = 0) \end{cases},$ (11)

$F_{2} (x, y, z) = {\begin{cases} {{\frac{1}{y} \arctan [\frac{x}{y} \frac{z - z_{0}}{\sqrt{x^{2} + y^{2} + {(z - z_{0})}^{2}}}]} |}_{z_{0} = 0}^{z_{0} = h}, (y \neq 0) \\ 0, (y = 0) \end{cases} .$ (12)

其中， ${{f (x, y, z, z_{0})} |}_{z_{0} = 0}^{z_{0} = h}$ 表示整个 ${f (x, y, z, z_{0})}$ 表达式中 $z_{0}$ 分别取值h和0时的差值。

同理，可计算其余载流导体在场点P(x,y,z)处产生的磁通量密度。则由磁场叠加原理整理得到图1所示六边形永磁体的磁通量密度的解析表达式为

$\begin{matrix} B_{x} = K [F (y - y_{3}, x - x_{3}, z) - F (y - y_{2}, x - x_{3}, z) + F (y - y_{2}, x - x_{1}, z) - F (y - y_{3}, x - x_{1}, z) \begin{matrix} \end{matrix} \\ + T_{1} (F (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{3}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z)) \end{matrix}$

$\begin{matrix} + T_{1} (F (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{1}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z)) \\ + T_{1} (F (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{1}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z)) \\ + T_{1} (F (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{3}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z))], \end{matrix}$ (13)

$\begin{matrix} B_{y} = K [T_{2} (F (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{3}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z)) \\ + T_{2} (F (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{1}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z)) \\ + T_{2} (F (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{1}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z)) \\ + T_{2} (F (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{3}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z) - F (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z))], \end{matrix}$ (14)

$\begin{matrix} B_{z} = K [F_{1} (y - y_{2}, x - x_{3}, z) - F_{1} (y - y_{3}, x - x_{3}, z) + F_{1} (y - y_{3}, x - x_{1}, z) - F_{1} (y - y_{2}, x - x_{1}, z) \begin{matrix} \end{matrix} \\ + G_{2} (F_{2} (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z) - F_{2} (\sqrt{1 + k^{2}} (\frac{x + k b - k y}{1 + k^{2}} - x_{3}), \frac{k x + y - b}{\sqrt{1 + k^{2}}}, z)) \\ + G_{3} (F_{2} (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{1}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z) - F_{2} (\sqrt{1 + k^{2}} (\frac{x - k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y + b}{\sqrt{1 + k^{2}}}, z)) \\ + G_{5} (F_{2} (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{2}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z) - F_{2} (\sqrt{1 + k^{2}} (\frac{x - k b - k y}{1 + k^{2}} - x_{1}), \frac{k x + y + b}{\sqrt{1 + k^{2}}}, z)) \\ + G_{6} (F_{2} (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{3}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z) - F_{2} (\sqrt{1 + k^{2}} (\frac{x + k b + k y}{1 + k^{2}} - x_{2}), \frac{k x - y - b}{\sqrt{1 + k^{2}}}, z))] . \end{matrix}$ (15)

其中，

${\begin{cases} G_{2} = \frac{y + k x - b}{\sqrt{1 + k^{2}}}, G_{3} = \frac{y - k x - b}{\sqrt{1 + k^{2}}} \\ G_{5} = \frac{y + k x + b}{\sqrt{1 + k^{2}}}, G_{6} = \frac{y - k x + b}{\sqrt{1 + k^{2}}} \end{cases},$ (16)

${\begin{cases} x_{1} = - \sqrt{3} a \\ x_{2} = 0 \\ x_{3} = \sqrt{3} a \\ K = \frac{μ_{0} J}{4 π} \end{cases},$ (17)

${\begin{cases} y_{1} = - 2 a \\ y_{2} = - a \\ y_{3} = a \\ y_{4} = 2 a \end{cases},$ (18)

${\begin{cases} T_{1} = \frac{k}{\sqrt{1 + k^{2}}} \\ T_{2} = \frac{1}{\sqrt{1 + k^{2}}} \end{cases} .$ (19)

2.3. 八边形永磁体

图3、图4分别为八边形永磁体的三维分子环流模型和二维解析模型。永磁体的高度为h₁mm，边长为a₁mm，其磁化电流密度为J₁。设图4中斜线的斜率为k₁，截距为b₁，x_i(i = 4, 5, 6, 7)和y_j(j = 5, 6, 7, 8)为其各坐标顶点。遵循上述解析过程，且定义如(21)~(23)式所示的系数，则图3所示的八边形永磁体的磁通量密度的由(24)~(26)式描述。

Figure 3. 3D molecular circulation model of octagonal permanent magnet

图3. 八边形永磁体的三维分子环流模型

Figure 4. 2D analytical model of octagonal permanent magnet

图4. 八边形永磁体的二维解析模型

${\begin{cases} {G^{'}}_{2} = \frac{y + k_{1} x - b_{1}}{\sqrt{1 + k_{1}^{2}}}, G_{4} = \frac{y - k_{1} x - b_{1}}{\sqrt{1 + k_{1}^{2}}} \\ {G^{'}}_{6} = \frac{y + k_{1} x + b_{1}}{\sqrt{1 + k_{1}^{2}}}, G_{8} = \frac{y - k_{1} x + b_{1}}{\sqrt{1 + k_{1}^{2}}} \end{cases},$ (20)

${\begin{cases} x_{4} = - (\sqrt{2 + 1}) a_{1} \\ x_{5} = - a_{1} \\ x_{6} = a_{1} \\ x_{7} = (\sqrt{2 + 1}) a_{1} \end{cases},$ (21)

${\begin{cases} y_{5} = - (\sqrt{2 + 1}) a_{1} \\ y_{6} = - a_{1} \\ y_{7} = a_{1} \\ y_{8} = (\sqrt{2 + 1}) a_{1} \end{cases},$ (22)

${\begin{cases} T_{3} = \frac{k_{1}}{\sqrt{1 + k_{1}^{2}}} \\ T_{4} = \frac{k_{1}}{\sqrt{1 + k_{1}^{2}}} \\ K_{1} = \frac{μ_{0} J_{1}}{4 π} \end{cases} .$ (23)

$\begin{matrix} B_{x} = K_{1} [F (y - y_{7}, x - x_{7}, z) - F (y - y_{6}, x - x_{7}, z) + F (y - y_{6}, x - x_{4}, z) - F (y - y_{7}, x - x_{4}, z) \begin{matrix} \end{matrix} \\ + T_{1} (F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{7}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{6}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + T_{1} (F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{5}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + T_{1} (F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{5}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + T_{1} (F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{7}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{6}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z))], \end{matrix}$ (24)

$\begin{matrix} B_{y} = K_{1} [F (x - x_{5}, y - y_{8}, z) - F (x - x_{6}, y - y_{8}, z) + F (x - x_{6}, y - y_{5}, z) - F (x - x_{5}, y - y_{5}, z) \begin{matrix} \end{matrix} \\ + T_{2} (F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{6}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{7}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + T_{2} (F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{5}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \end{matrix}$

$\begin{matrix} + T_{2} (F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{5}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + T_{2} (F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{7}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{6}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z))], \end{matrix}$ (25)

$\begin{matrix} B_{z} = K_{1} [F_{1} (y - y_{2}, x - x_{4}, z) - F_{1} (y - y_{3}, x - x_{4}, z) + F_{1} (x - x_{2}, y - y_{4}, z) - F_{1} (x - x_{3}, y - y_{4}, z) \begin{matrix} \end{matrix} \\ + F_{1} (y - y_{3}, x - x_{1}, z) - F_{1} (y - y_{2}, x - x_{1}, z) + F_{1} (x - x_{3}, y - y_{1}, z) - F_{1} (x - x_{2}, y - y_{1}, z) \\ + {G^{'}}_{2} (F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{3}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x + y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + G_{4} (F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} k y}{1 + k_{1}^{2}} - x_{1}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{2}), \frac{k_{1} x - y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + {G^{'}}_{6} (F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{2}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x - k_{1} b_{1} - k_{1} y}{1 + k_{1}^{2}} - x_{1}), \frac{k_{1} x + y + b_{1}}{\sqrt{1 + k_{1}^{2}}}, z)) \\ + G_{8} (F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{4}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z) - F_{2} (\sqrt{1 + k_{1}^{2}} (\frac{x + k_{1} b_{1} + k_{1} y}{1 + k_{1}^{2}} - x_{3}), \frac{k_{1} x - y - b_{1}}{\sqrt{1 + k_{1}^{2}}}, z))] . \end{matrix}$ (26)

其中，函数符号F、F₁、F₂同上，仅需将 ${{f (x, y, z, z_{0})} |}_{z_{0} = 0}^{z_{0} = h}$ 中h变换为h₁即可。

3. 有限元仿真验证

在MATLAB 2021a中建立了(15)和(26)式的数值分析模型，得到六边形永磁体和八边形永磁体外部空间磁场分布的数值分析结果。在有限元仿真分析软件ANSYS 2020R2中，分别建立了六边形永磁体和八边形永磁体的三维仿真模型，得到二者外部空间磁场分布的有限元分析结果。仿真参数设置见表1。通过对比有限元分析和数值分析的结果来验证(15)和(26)式的正确性。

在MATLAB 2021a中建立(15)和(26)式的数值分析模型时，首先需定义用于解析B_z分布的(11)和(12)式以及(15)和(26)式中所用参数。其次，每次循环都需计算每一条载流导体在场点P(x,y,z)处产生的B_z值，并进行加和。最后，经过多次循环，得到永磁体在一条线处所产生的B_z分布。两种方法的对比结果见图5、图6。

Table 1. Simulation parameters

表1. 仿真参数

图5表明，由(15)式得到的磁通量密度的法向分量B_z能很好地吻合有限元分析的结果。即本文所推导的六边形永磁体的磁场分布的解析表达式是正确的。图6表明，由(26)式得到的磁通量密度的法向分量B_z分布趋势与有限元分析的结果整体上是一致的。但在图形的顶部，有限元分析的结果存在毛刺，这是由于仿真过程中的数值噪声引起的。此外，由于有限元仿真中边界条件的选取和网格的划分等，导致曲线两端的幅值存在较大的误差，两端的波形并未完全重合。但这些偏差都是有限元分析中合理的存在，故本文所推导的六边形、八边形永磁体磁场的数值表达式是正确的。

Figure 5. Magnetic field distribution of hexagonal permanent magnet

图5. 六边形永磁体的磁场分布

Figure 6. Magnetic field distribution of octagonal permanent magnet

图6. 八边形永磁体的磁场分布

4. 八边形永磁体的三维磁场分布特性

为研究八边形永磁体的分布特性，对比分析了八边形永磁体和矩形永磁体的磁场分布特性。参数设置见表2。图7是二者在平面R²上的三维磁场对比结果，图8是八边形永磁体在线x= 2 mm，y= [−2.4142, 2.4142] mm上的磁场分布。

Table 2. Parameter settings of octagonal and rectangular permanent magnet

表2. 八边形和矩形永磁体的参数设置

图7中，八边形永磁体和矩形永磁体B_x、B_z的分布趋势一致；八边形永磁体B_y的幅值较小，且其波形与矩形永磁体的相差半个周期；二者B_z的峰值均是三个分量中最大的。图8也表明，在相同位置，八边形永磁体和矩形永磁体B_x的分布波形相似，八边形永磁体的分布波形具有更好的正弦性，而矩形永磁体的幅值较大；二者B_y的分布相差半个周期；二者B_z间的差值稳定。综上，虽然八边形永磁体的磁通量密度的幅值较小，但其波形的正弦性更好，且其B_z的幅值是三个分量中最大的，与B_x、B_y的差值较大，其磁场的综合分布特性较矩形永磁体的好。

Figure 7. 3D magnetic field distribution of octagonal and rectangular permanent magnets

图7. 八边形和矩形永磁体的三维磁场分布

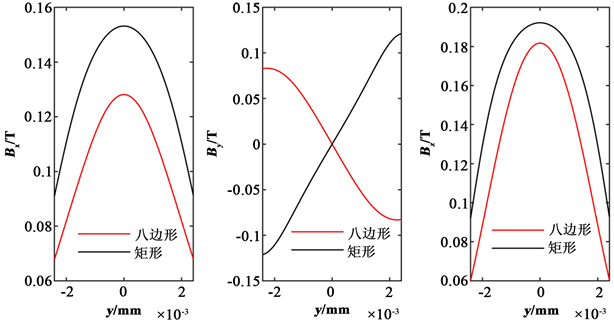
Figure 8. Magnetic field distribution of octagonal and rectangular permanent magnets

图8. 八边形和矩形永磁体的磁场分布

5. 结论

有限元分析结果验证了本文全参数化的数值表达式的有效性，有助于多边形永磁体结构的动力学建模和仿真。磁场分布的对比结果表明，八边形永磁体较矩形永磁体具有更好的磁场分布特性。结合坐标变换，本文的研究结果可解析任意磁化方向和任意放置方式的棱柱形永磁体的磁场。此外，也可为今后的研究提供更多的永磁体形状选择和理论依据。

NOTES

^*通讯作者。

参考文献

[1]	闫梁, 万本例, 胡斌, 等. 基于双轴TMR电磁传感器的裂纹检测方法研究[J]. 仪器仪表学报, 2021, 42(9): 106-114. https://doi.org/10.19650/j.cnki.cjsi.J2108082
[2]	余亚东, 宋凯, 李光海, 等. 多通道低频电磁传感器的仿真及优化[J]. 仪器仪表学报, 2019, 40(10): 19-27. https://doi.org/10.19650/j.c-nki.cjsi.J1905644
[3]	Han, D., Shinshi, T., Aauma, N., et al. (2019) An In-Plane, Large-Stroke, Multipole Electromagnetic Microactuator Realized by Guideways Stacking Mechanism. Sensors and Actuators A: Physical, 298, Article ID: 111563. https://doi.org/10.1016/j.sna.2019.111563
[4]	Tisnes, S.D., Shi, Z., Herth, E., et al. (2020) Long-Range Planar Conveyance Device Based on a Digital Electromagnetic Actuator Array. 2020 Symposium on Design, Test, Integration & Packaging of MEMS and MOEMS (DTIP), Lyon, 15-26 June 2020, 1-5. https://doi.org/10.1109/DTIP51112.2020.9139157
[5]	徐奇伟, 龙胜, 程智浩, 张艺璇, 支钞. 基于改进粒子群算法的微直线电机动子位置辨识策略研究[J]. 电机与控制学报, 2021, 25(8): 56-66. https://doi.org/10.15938/j.emc.2021.08.007
[6]	Furlani, E.P. (2001) Permanent Magnet and Electromechanical Devices—Materials, Analysis and Applications. Academic Press, San Diego, 212-216. https://doi.org/10.1016/B978-012269951-1/50005-X
[7]	苟晓凡, 杨勇, 郑晓静. 矩形永磁体磁场分布的解析表达式[J]. 应用数学和力学, 2004(3): 271-278.
[8]	刘宏娟. 矩形永磁体三维磁场空间分布研究[D]: [硕士学位论文]. 北京: 北京工业大学, 2006.
[9]	段家珩, 张昆仑, 罗成, 黎松奇. 梯形Halbach永磁阵列空心直线同步电动机特性的解析计算与优化[J]. 电机与控制应用, 2018, 45(10): 59-65+72.
[10]	Janssen, J.L.G., Paulides, J.J.H. and Lomonova, E.A. (2010) 3D Analytical Field Calculation Using Triangular Magnet Segments Applied to Askewed Linear Permanent Magnet Actuator. Compel, 29, 984-993. https://doi.org/10.1108/03321641011044406
[11]	Deshmukh, A., Petit, L., Khan, M.U., et al. (2017) Development of a Six Positions Digital Electromagnetic Actuator. 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, 3-7 July 2017, 975-980. https://doi.org/10.1109/AIM.2017.8014145
[12]	Deshmukh, A., Petit, L., Khan, M.U., et al. (2018) A Novel Three-Dimensional Electromagnetic Digital Actuator with 12 Discrete Positions. IEEE/ASME Transactions on Mecha-tronics, 23, 1653-1661. https://doi.org/10.1109/TMECH.2018.2841014
[13]	Deshmukh, A., Petit, L., Khan, M.U., et al. (2018) Stick-Slip Conveyance Device Based on a Hexagonal Digital Electromagnetic Actuator. 2018 12th France-Japan and 10th Eu-rope-Asia Congress on Mechatronics, IEEE, Tsu, 10-12 September 2018, 174-179. https://doi.org/10.1109/MECATRONICS.2018.8495712
[14]	Deshmukh, A., Petit, L., Khan, M.U., et al. (2019) A Micro-Fabricated Hexagonal Digital Electromagnetic Actuator. 2019 IEEE/ASME International Conference on Ad-vanced Intelligent Mechatronics (AIM), Hong Kong, 8-12 July 2019, 44-49. https://doi.org/10.1109/AIM.2019.8868822
[15]	Deshmukh, A., Petit, L., Khan, M., et al. (2021) Planar Mi-cro-Positioning Device Based on a 3D Digital Electromagnetic Actuator. Actuators, 10, 310. https://doi.org/10.3390/act10120310
[16]	Celik, S. and Kural, M.H. (2018) Octagonal Halbach Magnet Array Design for a Magnetic Refrigerator. Heat Transfer Engineering, 39, 391-397. https://doi.org/10.1080/01457632.2017.1305846
[17]	Ergor, M. and Bingolbali, A. (2022) Field-Free Line Mag-netic Particle Imaging Magnet Design Using Nested Halbach Cylinders. IEEE Magnetics Letters, 13, 1-4. https://doi.org/10.1109/LMAG.2022.3159446
[18]	马海武. 电磁场理论[M]. 北京: 清华大学出版社, 2016.
[19]	Gradshteyn, I.S. and Ryzik, I.M. (1994) Table of Integrals, Serie, and Products. 5th Edition, The Academic Press, London, 97-98.

为你推荐

友情链接