1. 引言
金融市场在国家经济体系中扮演着至关重要的角色,金融市场的表现反映着国家经济发展状态,挖掘金融市场变化的潜在规律并准确的判断金融市场的发展趋势,有利于相关从业者制定更完善的策略,达到降低风险,提高效益的目的 [1]。
一直以来,股票在金融市场中有着举足轻重的地位,而股票价格往往对时间因素非常敏感 [2],所以建立时间序列模型能有效地对股票价格进行预测。本文选取深粮控股的收盘价历史数据,采用ARIMA模型,对未来几天的收盘价进行预测。
2. ARIMA模型原理
ARIMA模型即差分移动平均自回归(Autoregressive Integrated Moving Average)模型,主要被用于拟合具有平稳属性的时间序列,或者是可以转换为具有平稳属性的时间序列,是目前广泛为学者应用的时间序列拟合方法 [3]。其中心思想是通过差分运算法使得不平稳的原始序列趋于平稳,其中d为差分运算的总次数。基本原理如下:
(1)
其中,
;
、
分别为平稳可逆ARIMA(p,q)模型的自回归系数多项式和移动平均系数多项式。其中自回归(AR(p))、移动平均(MA(q))、自回归移动平均(ARMA(p,q))模型都是ARIMA(p,d,q)模型的一个特例。当
且
时,ARIMA(p,0,0)即为AR(p)模型;当
且
时,ARIMA(0,0,q)即为MA(q)模型;当
且
时,ARIMA(p,0,q)即为ARMA(p,q)模型 [4]。ARIMA模型的性质见下表1:

Table 1. ARIMA(p,d,q) fixed-order rules
表1. ARIMA(p,d,q)定阶规则
3. ARIMA模型构建
大致来讲,ARIMA模型构建大约需要几个步骤,如下图1所示:
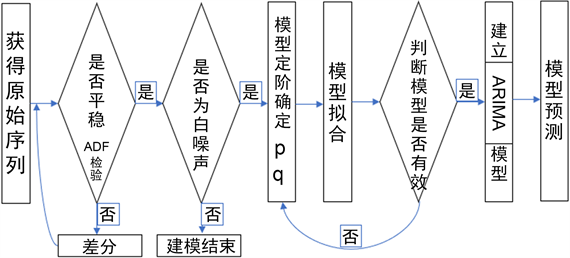
Figure 1. Flow chart of ARIMA model construction
图1. ARIMA模型构建流程图
平稳性检验。时间序列的平稳性代表时间序列的统计性质关于时间平移的不变性。对原始股票价格数据进行平稳性检验时,如果数据为非平稳时间序列,需要对序列进行差分运算,直至序列平稳 [5]。
白噪声检验(纯随机性检验)。序列的各项数值之间不相关,序列在进行完全无序的随机波动,这样的序列称为纯随机时间序列(白噪声序列)。纯随机时间序列是没有信息可提取的序列,如果序列为白噪声序列,应当停止分析 [6]。
模型定阶(模型识别)。结合数据样本时序图和AIC信息准则,确定模型自回归系数p和移动平均系数q的最优组合 [7]。
模型拟合。根据已经确定的最优参数p和q,对平稳非白噪声时间序列进行拟合,构建ARIMA(p,d,q)模型。
模型检验。对模型进行显著性(有效性)检验,检验模型是否将样本信息进行充分提取。当模型检验为无效模型时,重复步骤三,直至模型有效 [8] [9]。
3.1. 数据描述
本实验所采集数据均来自tushare金融大数据社区,通过python连接API接口获得。实际选取了深粮控股的收盘价2021年12月6日至2022年7月15日共147个数据样本。
3.2. 数据预处理
为保证数据的可靠性和有效性,本文数据全部选自tushare金融大数据社区,然后对其缺失值和异常值进行了处理,对缺失值全部采用上一个交易日的数据,对异常值作删除处理。
3.3. 模型构建
首先,对原始数据进行平稳性检验,观察原序列的时序图如图2所示。
观察图2,可见其为非平稳序列,不过为避免肉眼观察的主观性,再对原始序列进行ADF单位根检验。即序列若存在单位根,则不平稳。ADF单位根检验结果如表2所示,由表可知,检验统计量
,且
,不能拒绝原假设,故判断原序列非平稳。
ARIMA模型建模要求必须为平稳的时间序列,因此对原序列进行一阶差分,再对一阶差分后的序列进行ADF检验,结果如表3所示:
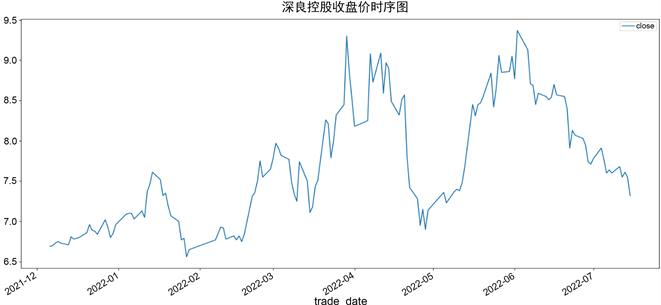
Figure 2. Original data time series diagram
图2. 原始数据时序图

Table 2. Results of the original series ADF test
表2. 原序列ADF检验结果

Table 3. Results of the ADF test for the series after first-order differencing
表3. 一阶差分后序列ADF检验结果
观察图3差分后序列已平稳,由表3,检验统计量
,且
,拒绝原假设,故判断序列平稳,可以用于建模。
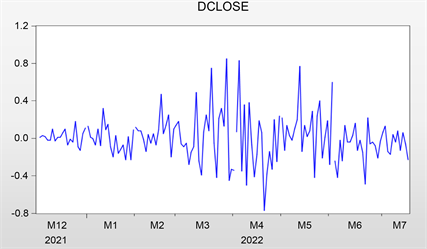
Figure 3. Timing diagram of the sequence after first-order differencing
图3. 一阶差分后序列时序图
一阶差分后序列平稳,故确定
,模型的定阶就是估计自回归阶数p和移动平均阶数q的过程。图4为差分后序列的自相关和偏自相关图,观察图4可知,ACF和PACF均拖尾,判断为ARMA模型,初步判断取
。为进一步确定更合适的p和q取值,运用AIC信息准则估计不同阶数对模型拟合精度的影响,如表4所示,综合结果选择
,建立ARIMA(5,1,5)模型。

Figure 4. Differential post-sequence ACF and PACF plots
图4. 差分后序列ACF和PACF图

Table 4. AIC values corresponding to different orders
表4. 不同阶数对应的AIC值
根据上文,建立ARIMA(5,1,5)模型进行拟合,结果如图5所示,模型对应的
,故模型显著有效。进行参数估计,并写出对应表达式为:
(2)
3.4. 模型的显著性检验
模型的显著性检验主要检验模型的有效性,即拟合模型是否充分提取观测值序列中所有的样本相关信息。当拟合模型为有效模型时,残差序列
不存在任何相关性,即残差序列
为白噪声序列。对模型进行残差检验,由图6,
,故不能拒绝原假设,即残差为白噪声序列,模型显著有效。
此外,DW(Durbin_Waston)检验也是检验残差的自相关方法 [2]。检验统计量DW的取值范围为区间[0, 4],DW趋近于0,序列显著正相关;DW趋近于4,序列显著负相关;DW趋近于2,序列不存在自相关性。经检验得,DW = 2.13趋近于2,因此可判断残差为白噪声序列。
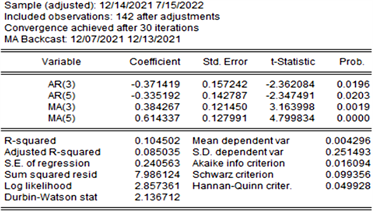
Figure 5. ARIMA(5,1,5) fitting result
图5. ARIMA(5,1,5)拟合结果
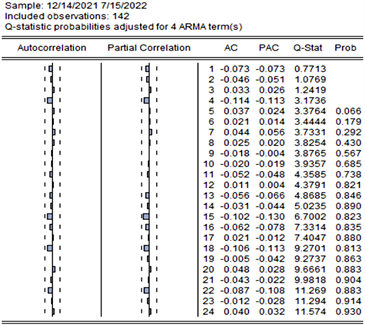
Figure 6. Residual series autocorrelation plot
图6. 残差序列自相关图
观察图7,模型的残差序列值基本拟合在直线y = 0附件呈对称分布,因此,也可判断残差序列不存在自相关。
3.5. 模型预测结果分析
由表5可知,由上表可知,预测误差率均控制在5%以内,虽仍有些许误差,但预测值的误差相对较小,在可控范围内,即认为该模型具有较好的拟合效果。
4. 结语
股票价格预测一直备受瞩目,本文采用ARIMA对所选取的数据样本进行了预测,介绍了建模的基本方法和步骤,通过平稳性,白噪声等检验,构建了ARIMA并进行了预测。结果表明,该预测方法是可靠的,对原序列信息提取充分,拟合效果较好。但也看到预测值较真实值偏小,且预测期数越长误差越大。因此相关从业者可选择此方法进行短期预测,以为其相关投资决策作为参考。