1. 引言
目前国内外采用透明土技术和渗流从事科学实验研究的领域已经有很多,随着透明土技术被不断应用到学术研究中来,国内外在透明土的研究上也取得了不少成就。在浅基础地基渗透和承载力研究方面,Sadek与Liu利用了模型实验与光学观测方法对天然土体与透明土在相同模型条件下的实验结果进行了对比分析。在深基础及结构和土体相互作用方面,Song等将透明土应用于离心模型实验中,对锚板在嵌入黏土过程中的锚固力损失进行了分析。Ni等利用透明土实验技术对成桩过程中桩与桩周土的相互作用做了研究。
渗透系数K是综合反映土体渗透能力的一个指标,其数值的确定对渗透计算有着非常重要的意义。目前渗透系数的获取和分析也变得越来越重要,例如据相关资料显示 [1] [2],多数基坑安全事故是由渗透作用造成的,这与渗透系数的关系密不可分。在渗透系数研究方面,Hazen [3] [4] 最早给出了均质无粘性砂土渗透系数与颗粒有效粒径呈二次函数关系的经验性数学表达,拟合常数的取值根据介质的不同而有差异,有时可达3个数量级。由于将介质的结构特征和流体物理属性综合反映在一个抽象的拟合常数中,因此Hazen模型最初仅适合一般的工程应用 [5] [6]。后期的研究通过对常数项赋予更多的结构性参数表达,如根据平行毛细管道模型建立的Kovacs [7] 模型,其提供了对该常数项结构性参数的解释,从而丰富了Hazen模型的物理内涵。为克服Hazen公式的缺陷,Kozeny [8] 和Carman [9] 建立了半经验半理论的Kozeny-Carman公式,发展出了与宏观统计参数(孔隙度、比面)和细观孔隙结构特征参数(分形维数、毛管迂曲度)表达的渗透毛细阻力模型 [10]。该模型假设一簇毛管束组成的渗流通道,其渗流所产生的能量损耗来自流体流动过程,主要为克服毛管束迂回结构、表面摩擦及流体粘滞等阻力所做的功。该模型更深刻地揭露渗流过程的物理涵义,成为目前研究最深、变化形式最多、应用最广的渗流模型 [11] [12]。
基于特定的配置方法配制而成的透明土既有着与天然土相似的性质,又要有良好的透明性,而且稳定,不易于与其填充的混合液发生反应,也不会与示踪剂发生反应,是渗透实验中观察土体内部规律的良好材料。本文利用透明土模拟天然砾石土,并对其进行直接观测,通过透明土实验技术 [13] 设计相应的物理实验模型,实现对土体内部渗流等问题的可视化观测,从而获得直观的研究成果。同时将透明土实验所获得的实际参数与Kozeny-Carman公式、Kovacs公式、Amer-Award等模型公式相结合从而得到土体的渗透系数,最后通过计算所得渗透系数之间的对比,探索其随土体自身物理特征变化而变化的趋势和规律。
2. 渗透系数计算公式
2.1. Kovacs公式(经典水力学公式)
Kovacs公式是根据平直管道模型(如图1所示) [14] 建立的,它提供了对该常数项结构性参数的解释,丰富了此前的Hazen模型的物理内涵。其计算公式为:
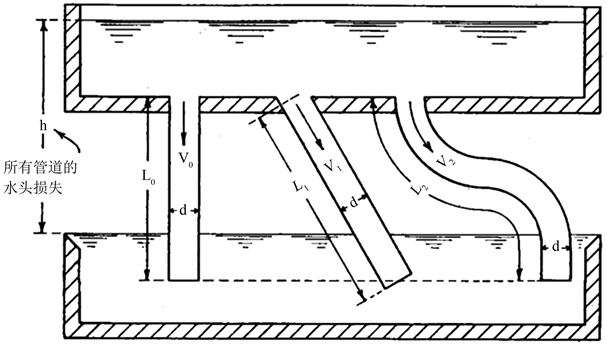
Figure 1. K-C formula bending pipe model diagram
图1. K-C公式弯曲管道模型图
(1)
公式中K为渗透系数(cm/s),d0被称为最小等效孔隙粒径(mm),
,该表达式中n为孔隙率,μw是水的动力粘滞系数(N·s/m2),α为土的形状系数,Dh为等效直径(mm),
其中Di是第i级粒径区间的平均粒径(mm);Δsi为第i级粒径的重量与样本总重量之比。该公式也被称为经典水力学公式。
2.2. Amer-Award公式
Amer、Award等 [15] 考虑了土体内部孔隙和不均匀系数对渗透系数的影响,对上述公式进行了修正,其表达式为:
(2)
其中e为孔隙比,由孔隙率n计算得出,计算公式为
,Cu为不均匀系数
,其中d60为颗粒累计百分含量为60%时对应的粒径,也称为限制粒径;d10为颗粒累计百分含量为10%时对应的粒径,也称为有效粒径;均可通过透明土的颗粒级配曲线获得。
2.3. Kozeny-Carman公式
Kozeny和Carman建立了半经验半理论的Kozeny-Carman公式(也可简称为K-C公式),从而发展出了与宏观统计参数(孔隙度、比面)和细观孔隙结构特征参数(分形维数、毛管迂曲度)表达的渗透毛细阻力模型。该模型假设一簇毛管束组成的渗流通道,其渗流所产生的能量损耗来自流体流动过程,主要为克服毛管束迂回结构、表面摩擦及流体粘滞等阻力所做的功(弯曲管道模型如图1所示)。该公式考虑了土体内部孔隙的弯曲状况等因素因此更加具有普遍意义。其公式为
(3)
其中所得值k为渗透率,τ为迂曲度,s为比面(cm3/cm2)。
,
,其中Le为流体在土体中的实际渗流路径长度,L0为土体的垂直高度。比面计算公式
,n为孔隙度,di为砾石所对应直径。
吴金随等通过流体平均水力半径模型建立了迂曲度与孔隙率、渗透率、平均粒径间的函数关系,揭示出更多的迂曲度的影响因素。其公式为
(4)
其中k为渗透率(md),Dp为平均粒径(mm),通过下述透明土实验所得迂曲度带入式(4)并与式(5)进行循环迭代最终得到渗透率和迂曲度的最佳值。
计算K-C公式的渗透系数K公式为
(5)
其中
为流体的密度(kg/m),g为重力加速度(m/s2),
为流体的动力粘滞系数(N∙s/m2)。
实验主要采用Kovacs公式、Amer-Award公式以及K-C公式进行渗透系数的计算,图2为上述三个公式管道模型剖面展示图。
Figure 2. Formula pipe model display diagram
图2. 公式管道模型展示图
3. 透明土渗透模拟实验
3.1. 样品制备及物理特征
透明土土骨架材料既要有天然土相似的性质,又要有良好的透明性,而且稳定,不易于与其填充的混合液发生反应,也不会与示踪剂发生反应,材料的密度与所要研究的土的密度大致相近,在真空除气时耐高压,在水洗烘干中能承受一定的高温,石英砂颗粒能回收重复利用。高纯度的熔融石英是用天然高纯度的二氧化硅经过高温度熔融,然后快速冷却而获得,而本文所使用的熔融石英砂是从熔融经过冷却击碎后,人工拣选透明度更高的,纯度更好的。
本文所采用的石英砂粒径为0.75~10 mm,通过筛分法依次用5 mm、2 mm、1 mm、0.5 mm、0.25 mm、0.1 mm、0.075 mm的标准筛筛分熔融石英砂。经计算配比配置细颗粒含量30%、32%、34%的石英砂粒模拟砾石土进行渗透实验。实验用熔融石英砂颗粒粒径如图3所示,实验用示踪剂及透明土溶液如图4所示。
土壤颗粒往往以2 mm的颗粒粒径作为颗粒粗细的区分粒径。本实验配制以0.075~2 mm粒径的透明熔融石英砂作为细颗粒和以2~10 mm粒径透明熔融石英砂作为粗颗粒混合构成的9种不同的级配不连续透明土,将其分为三组。第一组是细颗粒粒径0.25~0.5 mm缺失且细颗粒含量分别为30%、32%、34%的透明土A、B、C;第二组是细颗粒粒径0.5~1 mm缺失且细颗粒含量分别为30%、32%、34%的透明土D、E、F;第三组是细颗粒粒径1~2 mm缺失且细颗粒含量分别为30%、32%、34%的透明土J、H、I。实验所用透明土的颗粒级配曲线如图5所示,物理特征参数见表1。

Figure 3. Fused quartz sand particles of various sizes used in the experiment
图3. 实验用各粒径熔融石英砂颗粒

Figure 4. Potassium permanganate tracer (left) and transparent soil solution (right)
图4. 高锰酸钾示踪剂(图左)及透明土溶液(图右)

Table 1. Physical characteristic parameters of each group of transparent soil
表1. 各组透明土物理特征参数
 (a)
(a) (b)
(b) (c)
(c)
Figure 5. Gradation curve of transparent soil in each group. (a) 0.25~0.5 mm deletion group; (b) 0.5~1 mm deletion group; (c) 1~2 mm deletion group
图5. 各组透明土颗粒级配曲线图。(a) 0.25~0.5 mm缺失组;(b) 0.5~1 mm缺失组;(c) 1~2 mm缺失组
3.2. 实验装置及实验过程
本次实验的实验装置如图6(a)所示,实验装置由医用输液瓶、输液管(用于控制示踪剂溶液流速及保持实验容器中透明溶液剂量不变)、透明土渗流实验置以及摄影支架、摄影幕布等部分组成。
装置主要用于透明土渗透模拟实验,旨在通过示踪剂在透明土的流动模拟流体在土体孔隙中的运移过程,记录并分析其渗流路径,以用于计算水体的迂曲度。实验使用透明亚克力板加工制作而成的10 * 10 * 10 cm正方体容器来装载透明土。该容器的正下方中间开有一出水孔,用于制造上下压力差迫使液体向下渗流。实验过程中通过摄影设备录像及拍照等方式直观记录高锰酸钾示踪剂在配置好的透明土孔隙中的运动轨迹,然后运用专业建模软件Rhino 7对运动轨迹进行建模,建立渗流路径的三维立体模型;最后将建立好的模型导入工程CAD软件进行数据处理,获得土体迂曲度参数,以便下一步进行渗透系数的计算。
本次透明土管涌模拟实验的实验步骤如下所示:
 (a)
(a) (b)
(b) (c)
(c)
Figure 6. Experimental devices and achievements. (a) Distribution of experimental devices; (b) Side display of devices at the end of the experiment; (c) Three dimensional model building by Rhino7 software
图6. 实验装置及成果。(a) 实验装置分布;(b) 实验结束装置侧面展示;(c) Rhino7软件构建三维模型
1) 首先将不同粒径的熔融石英砂按不同比例混合,作为制备实验要求的颗粒级配土样原材料。接着将#15白油和正十三烷按一定比例混合,制备折射率为1.4585左右的实验溶液,此折射率下的溶液最适合本次实验的观察,最后制备高锰酸钾溶液作为示踪剂放置于输液瓶中。
2) 检查10 * 10 * 10 cm正方体容器是否漏液。完成后将配置好的级配透明土加入其中,接着缓慢倒入配置的折射率为1.4585左右的实验溶液。一边倒入一边用玻璃棒连续搅拌,以保证液面略高于石英砂颗粒表面,直至两者融合而成的混合溶液充满容器。
3) 将混合溶液置于真空饱和桶中,抽真空减少液体中的气泡。
4) 将透明土装置放置平稳并将装有示踪剂和折射率为1.4585左右的实验溶液的补给滴管插入融合的混合溶液中,以此保证混合溶液的液面始终高于透明土砂砾。
5) 于三个对角方向架设摄影幕布、摄影支架及摄影装置,一个对角方向上的设备与其他两个对角方向上设备在方向上均相差120˚,用于记录实验过程。
6) 布置完成以后,正式开始实验。首先拔去透明土装置下的木塞,然后打开实验溶液补给滴管开关,调节补给管流速,直至装置中混合溶液液面高度保持不变。
7) 当混合溶液高度稳定后,打开示踪剂滴管开关,匀速缓慢的注入示踪剂,并用摄像机录像、拍照,直至示踪剂从下部出水口流出为止,如图6(b)所示。
8) 将透明土实验所获得的图像使用Rhino 7软件进行描图、立体化等操作处理用以建立透明土渗流路径的三维立体可视化模型,如图6(c)所示。
9) 将模型导入工程CAD对模型进行数据处理可以得示踪剂在土体孔隙中的实际渗流路径Le,垂直渗流路径L0。之后可运用公式
计算土体的迂曲度
作为K-C公式计算渗透系数的参数。
4. 实验成果展示和分析
图7~9为透明土实验实现对土体内部渗流轨迹可视化观测成果以及使用Rhino7软件处理所得的透明土渗流路径的三维立体可视化模型展示。
将模型导入工程CAD软件,通过对其进行数据处理可以得示踪剂在土体孔隙中的实际渗流路径Le,垂直渗流路径L0。之后可运用公式
计算土体的迂曲度
。表2为透明土实验数据经过计算处理处理所得迂曲度参数展示。

Table 2. Display table of tortuosity parameters of each group of transparent soil
表2. 各组透明土迂曲度参数展示表
结合图7~9和表2分析,在透明土细颗粒含量逐渐增加情况下,0.25~0.5 mm缺失系列透明土内部渗流流动范围呈现逐渐缩小现象,土体内部迂曲度则相反呈现逐渐曲折趋0.5~1 mm缺失系列透明土内部渗流流动范围呈现逐渐扩大现象,土体内部迂曲度则相反呈现逐渐平直趋势,该现象和趋势与0.25~0.5 mm缺失系列透明土相反,土体内部迂曲度变化幅度大;1~2 mm缺失系列透明土内部渗流流动范围变化不明显,土体内部迂曲度变化幅度小。
5. 各组土样渗透系数公式值比较分析
将表1各系列透明土物理参数和表2各系列透明土实验参数作为Kovacs公式、Amer-Award公式以及K-C公式计算参数使用,代入各个公式中,最终获得各模型公式对应渗透系数值,如表3~5所示。

Table 3. Table of permeability coefficient values of each model formula of 0.25~0.5 mm missing group transparent soil
表3. 0.25~0.5 mm缺失组透明土各模型公式渗透系数值展示表

Table 4. Table of permeability coefficient values of each model formula of 0.5~1 mm missing group transparent soil
表4. 0.5~1 mm缺失组透明土各模型公式渗透系数值展示表

Table 5. Table of permeability coefficient values of each model formula of 1~2 mm missing group transparent soil
表5. 1~2 mm缺失组透明土各模型公式渗透系数值展示表
通过对比表3~5,可知在任一颗粒含量和级配缺失下的透明土中,K-C公式的渗透系数都最大,Amer-Award公式次之,Kovacs公式渗透系数最小。其次在同一颗粒粒径缺失级配透明土中,随着细颗粒含量的增加,渗透系数值逐渐减小。但是,在细颗粒含量相同的情况下,随着颗粒级配中缺失的粒径逐渐增大,各公式的渗透系数值呈现先增大后减小的趋势。
6. 结论
本文利用透明土模拟天然砾石土,并对其进行直接观测,通过透明土实验技术设计相应的物理实验模型,实现对土体内部渗流等问题的可视化观测,从而获得直观的研究成果。通过对研究成果进行分析,得出以下结论:
1) 通过配置与天然土性质相近的透明土,实现了土体内部渗流的可视化,并且通过透明土渗流现象进行建模,将模型导入CAD软件进行计算得出了土体的迂曲度参数。
2) 从上文渗流模型的流动范围和迂曲度的计算结果可知,在级配透明土中,粒径更小的细颗粒缺失时,渗流范围缩小,迂曲更加曲折;而在粒径更大的细颗粒缺失时则变化不明显。说明粒径更小的细颗粒缺失时对迂曲度的影响更大,对土体内部渗流影响更大。
3) 将所得迂曲度参数与其他土体性质参数一起代入三个渗透系数计算公式,可以得出在任一颗粒含量和级配缺失下的透明土中,K-C公式的渗透系数都最大,Amer-Award公式次之,Kovacs公式渗透系数最小;在同一颗粒粒径缺失级配透明土中,随着细颗粒含量的增加,渗透系数值逐渐减小。
4) 在细颗粒含量相同的情况下,随着颗粒级配中缺失的粒径逐渐增大,各公式的渗透系数值呈现先增大后减小的趋势。