1. 引言
镍基高温合金是高度复杂的合金,含有众多合金化元素。镍基高温合金的性能主要受γ相和γ'相影响,通过γ相和γ'相的析出得到强化 [1]。γ基体通常含有较大数量的固溶元素,其本质是包含这些固溶元素的连续分布的面心立方结构(fpp)的镍基奥氏体相。由于γ相所含的固溶元素与基体Ni的晶格常数(原子半径)差异会引发晶格畴变,从而阻碍位错作用,提高合金的强度 [2]。但γ相对合金的强化作用也远小于γ'相。γ'相与基体相同,均为面心立方结构,点阵常数与基体相近,并于基体共格,因此γ'相在基体中能呈细小颗粒状均匀析出,阻碍位错运动,而产生明显的强化作用。γ'相是A3B型金属间化合物,在镍基合金中,以Ni3Al最为常见。通过γ'相析出沉淀强化是最主要的强化机制。
在高温合金中,由于有着大量的γ相与γ'相,也就有了大量的相界面。镍基单晶高温合金在高温、高应力服役时,为释放γ与γ'相之间晶格错配度产生的应力,相界面上逐渐生成界面位错。同时γ相中运动位错在应力驱使下也会“铺”在相界面上,这两种位错的协同作用导致相界面位错网络的形成。相界面位错网络与镍基单晶高温合金性能有着密不可分的关系。然而界面在高温合金服役时不是一成不变的。随着合金升温、降温,γ'相缩小、长大,γ/γ'相界面的迁移十分普遍。即使温度稳定,高温高应力下γ/γ'相界同样存在迁移现象并伴随γ'相的粗化 [3]。
Fioon Dunne基于此讨论了不同γ'相下蠕变速率的变化趋势 [4]。
Dyson和Osgerby认为,在γ'相溶线温度时,攀移位错和滑移位错的数量以相同的形式存在。攀移位错被认为固定在沉淀相之上。稳态滑移位错的通量随沉淀相体积分数而变化。在γ'相溶线温度以上的钉扎过程是不同的,位错网的大小决定了钉扎距离 [5]。
镍基高温合金的“成分–微结构”关系,可以通过基于Calphad的热力学计算方法,根据合金的成分确定γ'强化相的含量;采用相场计算或元胞自动机等计算方法,可以确定γ'强化相的分布。另一方面,镍基高温合金“微结构–力学性能”关系,目前并没有成熟的计算方法。虽然通过第一原理计算,可以对材料的弹性模量、硬度等力学性能进行预测,但镍基高温合金设计中重点关注的高温蠕变行为,直接计算仍不现实。镍基高温合金“微结构–力学性能”关系的计算方法,确定需要基于材料的微观变形机制建立计及微结构因素的晶体塑性(包括蠕变和损伤演化)模型,并通过实验对模型中难以根据第一原理、热力学、动力学等计算方法确定的模型参数进行实验标定,然后基于此模型进行预测,从而形成基于第一原理、热力学计算、动力学计算和晶体塑性计算的多尺度材料设计方法。
在本文中,利用以上理论建立了相关的方程,并根据实验所的γ'相含量、分布和蠕变曲线,对模型参数进行了标定,并基于此模型,对不同γ'含量和分布的合金进行了蠕变性能的预测,以期为合金的设计提供参考。
2. 基础理论模型
Gibbs理论的模型是一个粘塑性的模型,认为应变率可由位错密度、Burgers矢量和位错滑移的速度来确定,即 [6]
(1.1)
其中,Burgers矢量以b表示,它用来定义形成一个位错的滑移矢量,从而以此量化位错引起的晶体畸变。它的大小表征了位错的单位滑移距离,方向与滑移方向一致。由于Burgers矢量是对晶体内的位错的直接表征,因此,Burgers矢量的大小体现了晶体中何处易出现形成位错以及在外力作用下位错运动的难易程度。Burgers矢量与位错的状态及弹性性质直接相关。如位错的应力场、应变能、受力状态、位错间的相互反应等均与其Burgers矢量有关。
位错滑移的速度v由统计力学的方法得到。固定位错的逃逸率Γ乘以位错在热激活后所通过的面积,再除以平均间隔位错的距离l,即可得到位错滑移的速度v,而固定位错的逃逸率Γ有 [7]:
(1.2)
式中kb为Bltzman绝对温度,ΔG即为将固定位错激活使位错滑移的Gibbs自由能的能差。ΔG可以由Helmholtz自由能与切应力所做功的差值求得,即
(1.3)
由此可以得到,位错滑移的平均速率:
(1.4)
综上,应变率可表示为
(1.5)
如果正向和反向激活事件同时发生,在对称的排列中,有
(1.6)
此时,模型的三个基础的构成中,Burgers矢量与位错滑移的速度都得到了确定。为了得到滑移位错的密度,我们先参考一下Dyson的相关理论。
当有沉淀相存在时,我们假设沉淀相均匀分布于合金中。Dyson认为,在位错密度中,总有一个很小的、几乎确定的动态分数,这部分的位错处于从爬升网络中“逃逸”的位置。
由这一理论,我们可以将滑移位错密度的变化率表示为:
(1.7)
式中,
为攀移位错的密度,
为滑移位错密度,
为沉淀相体积分数,vg为滑移位错的平均速度,xu为攀移位错可成功滑移的概率,
为沉淀相的间距,Γu为成功攀移的频数。右式的第一项对应滑移位错的密度,第二项对应被困住或固定的滑移位错的密度。
稳态下,滑移位错通量在粘性滑移率高时发生。单轴拉伸条件下的蠕变应变率为:
(1.8)
式中,ρ:位错的密度;M:Taylor数;Cj:位错割阶密度;Dv:基体扩散系数;σk:运动内应力。
可以看出,这一模型仅适用于沉淀相的体积分数有限的情况下。在没有沉淀相存在时,改模型所预测的蠕变应变率为零。在此方法的基础上,我们认为蠕变速率由滑移位错的平均速度决定,而滑移位错的平均速度又由钉扎滑移位错所产生的障碍物的性质以及使位错攀移所必需的热激活事件决定,并以此为基础对模型进行进一步的改进,以期在没有沉淀相存在时也能体现出Gibbs理论模型的特点。
当钉扎是由沉淀相的析出引起时,钉扎位错的密度与Dyson模型一致,但当钉扎固定在某个粒子上时,它出现在某个位置的概率只取决于粒子的大小。因此,滑移位错的产生并不取决于沉淀相的体积分数,而是由ρcxuΓu来确定。因此,滑移位错密度的变化率可以表示为:
(1.9)
而攀移位错在正确的位置开始滑移的概率为:
(1.10)
h可由Burgers矢量来代替。
从正确的位置成功完成滑移的概率为:
(1.11)
总的位错密度ρ可由滑移位错密度和攀移位错密度的加和表示。整理以后有:
(1.12)
如果考虑稳态,那么稳态时滑移位错的密度为零,此时,可简化为:
(1.13)
我们假设沉淀相以三维阵列排列,将之简化为球体的析出增大,那么稳态下滑移位错的密度可以推导为:
(1.14)
其中,
(1.15)
由此模型可以看出,与Dyson的模型不同,在该物理模型中,滑移位错的密度随沉淀相体积分数的增大而减小,当沉淀相体积分数增加至0.78时,滑移位错的密度减小为0。
我们考虑正向和反向激活造成的位错攀移,滑移速度可表示为:
(1.16)
而应变率应为:
(1.17)
将滑移位错的密度带入,有
(1.18)
对公式进行归一化处理,有
(1.19)
在熔线温度以下,沉淀相存在,且沉淀相会在高温下发生扩张。低于这一温度时,蠕变的速率主要受沉淀相大小影响。而在高于这一温度时,沉淀相不再影响,蠕变速率可以认为主要受位错网的钉扎和分离影响。而位错网的大小决定了钉扎的分离程度。因此,在这个模型中,应该有 [8]:
(1.20)
即在沉淀相存在的情况下,我们认为模型由导致钉扎分离较小的因素来控制。
基于以上理论模型,我们构建用于拟合、计算的高温蠕变损伤模型。
3. 建立微结构损伤模型
由上文可知,高温下,当沉淀相呈球形时,高温合金发生蠕变的蠕变变形速率可以表示为:
(3.1)
(3.2)
针对<100>方向的单轴蠕变拉伸,考虑到<110><111>滑移系的激活,蠕变应变率可以简化为:
(3.3)
即受位错密度、沉淀相尺寸、沉淀相体积分数、温度与位错滑移的速度影响的一个参数。
而在一定的温度范围内,基于该模型,我们引入损伤变量ω的演化,可以写出用于计算的蠕变损伤变形率公式:
(3.4)
(3.5)
(3.6)
(3.7)
同理,当沉淀相呈立方体形时,由沉淀相体积分数与其尺寸的对应关系所发生的变化,我们可以得到其蠕变损伤变形率的公式:
(3.8)
(3.9)
(3.10)
(3.11)
其中,
为
强化相的含量,rs为
强化相的平均尺寸;
为位错密度,随蠕变过程演变,本报告假设位错密度增加率和蠕变应变的增加率线性相关;
为随蠕变过程演化的损伤变量 [2],本报告假设蠕变过程中损伤演化率保持不变;b为位错伯格斯矢量,kb为波尔兹曼常数,为常数;
为位错运动的频率,∆F为位错运动的激活能,这两个参数连同位错演化的参数、损伤演化的参数需要根据实验标定。
上述模型中,包含与微结构相关的参数
强化相的体积分数
,强化相粒子平均尺寸rs。给定合金的成分,
和rs这两个参数可以通过热力学、动力学计算确定。另外还有不易计算,需要由实验标定的7个参数。
基于python语言,本报告编制了计及微结构的单晶高温合金蠕变计算及参数标定程序。本报告采用差分进化算法对参数进行标定。该算法是一类基于群体的自适应全局优化算法,由于其具有结构简单、容易实现、收敛快速、鲁棒性强等特点,因而被广泛应用于各个领域。差分进化算法的主要过程包括起始、突变、交叉和选择四个阶段。为了避免陷入局部最小值陷阱,产生的突变向量还要与原本的目标向量按照一定的规则交叉,得到的向量作为种群下一代的目标向量。这一交叉过程保证了扰动在全体搜索空间内发生,大大降低了优化计算进入局部最小值的风险。
根据某新型合金的蠕变数据(如图1所示)。所采用的标定试样
含量70%,强化相平均尺寸500 nm,实验温度1030℃,拉伸应力230 MPa。标定时根据一组模型参数计算得到蠕变曲线,与实验所的曲线进行最小二乘拟合,得到拟合最优的参数组作为模型参数(表1和表2)。
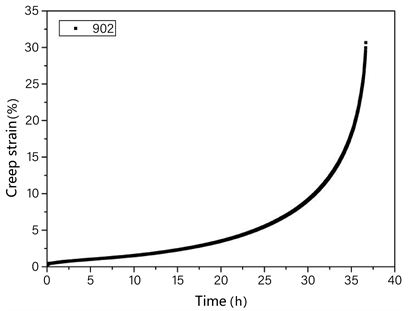
Figure 1. Creep curve of a nickel base single crystal superalloy
图1. 某镍基单晶高温合金的蠕变曲线

Table 1. Calibration of model parameters of cubic precipitation phase
表1. 立方体沉淀相模型参数的标定

Table 2. Calibration of model parameters of spherical precipitation phase
表2. 球体沉淀相模型参数的标定
下图给出了模型计算的蠕变曲线和实验曲线的拟合结果,从中可以看出,两者吻合的很好,说明成功进行了模型参数的标定,可以用来进行下一步微结构对蠕变性能影响的研究(图2)。

Figure 2. Fitting results of creep curve and experimental data
图2. 蠕变曲线和实验数据的拟合结果
4. 结果与分析
将我们所构建的考虑微结构与屈服应力变化的细化蠕变损伤模型的蠕变曲线与所得实验数据进行拟合,可以得到图3所示。
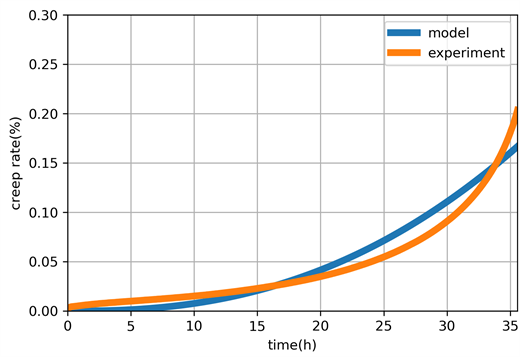
Figure 3. Fitting results of creep curve and experimental data
图3. 模型蠕变曲线和实验数据的拟合结果
显而易见,所构建的模型能很好的与实验数据相拟合。进一步的,我们对不同γ'含量和分布的合金进行蠕变性能的预测,以期为合金的设计提供参考。
对于析出相呈立方体形时,可绘制出当析出相尺寸为500 nm时,1030℃、230 MPa下的不同析出相体积分数的a新研合金蠕变曲线,如下图4所示:
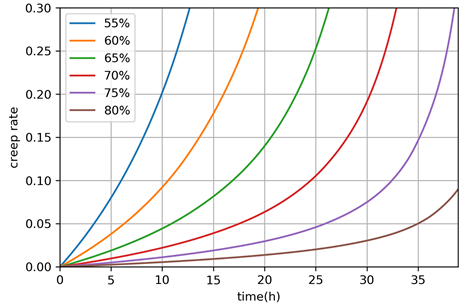
Figure 4. Creep curves of different volume fractions of cubic strengthened precipitated phase with the size of 500 nm
图4. 立方体强化相析出相尺寸为500 nm时不同析出相体积分数的蠕变曲线
同时,也可以绘制出当析出相体积分数为70%时,1030℃、230 MPa下的不同析出相尺寸下的a合金蠕变曲线(图5):

Figure 5. Creep curves of precipitated phase with different sizes when the volume fraction of cube reinforced phase is 70%
图5. 立方体强化相析出相体积分数为70%时不同析出相尺寸下的蠕变曲线
显而易见的,对于强化相为立方体形的镍基高温合金,由本模型所得出的不同析出相尺寸与体积分数下的蠕变曲线,可以做出以下预测:
同等条件下,在一定范围(强化相尺寸200 nm~800 nm;强化相百分比55%~80%内,强化相的尺寸越小,体积分数越大,其蠕变性能也就越好。
参照立方体形强化相的蠕变模型,可以认为,在这一范围内,当减小强化相的尺寸
,或增大体积分数
时,位错密度
会有显著的降低,因此其蠕变性能会有明显的提升。
进一步的,对强化相为球形时,1030℃、230 MPa工况的不同强化相尺寸与体积分数下的蠕变曲线进行预测,并与立方体形强化相下的蠕变曲线进行对比;因为球形析出相的高温合金其强化相体积分数一般最高不超过55%,故选取25%~50%的球形强化相高温合金总结其演化规律(图6)。
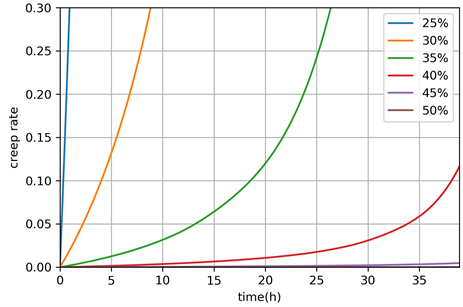
Figure 6. Creep curves of spherical reinforced phase with precipitation size of 500 nm
图6. 球形强化相析出相尺寸为500 nm时不同析出相尺寸下的蠕变曲线
从图7可以看出,与强化相呈立方体形析出时相同的是,当强化相呈球形时,在所选取的范围25%~50%内,强化相的体积分数越大,蠕变性能也就越好;在200 nm~800 nm的范围内,高温合金的蠕变性能都随强化相尺寸的减小而提高。而与立方体形强化相相对比可以看出,球形强化相的高温合金在同样的强化相含量与尺寸时,拥有更好的蠕变性能。
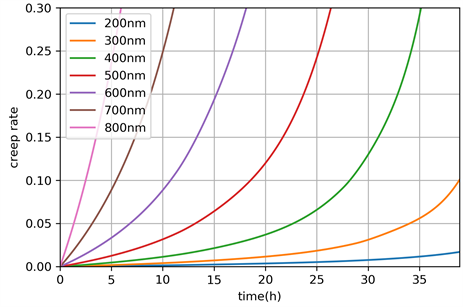
Figure 7. Creep curves of spherical reinforced precipitated phase with different sizes when the volume fraction is 35%
图7. 球形强化相析出相体积分数为35%时不同析出相尺寸下的蠕变曲线
从球形析出相的蠕变模型中可以看出,与立方体形析出相明显相同的是,在所选取的范围25%~50%内,强化相的体积分数
越大,位错密度
也就越小;而在200 nm~800 nm的范围内,球形强化相的高温合金也与立方体形强化相的高温合金一致,位错密度
随强化相尺寸
的减小而明显增加。因此,在不同的强化相体积分数与尺寸下,球形析出相的高温合金表现出了与立方体形析出相的高温合金相同的特性。
进一步的,以强化相为立方体形的镍基高温合金为例,选取更多的强化相尺寸与强化相体积分数进行预测,并观察与当前结论是否一致。
由图8可以总结出:当强化相呈立方体形时,在所选取的同样的范围55%~80%内,强化相的体积分数越大,蠕变性能也就越好;在200 nm~800 nm的范围内,高温合金的蠕变性能都随强化相尺寸的减小而提高。
由我们的模型,我们可以认为,在这些变化中,析出相的微结构的变化主要通过影响位错密度来影响蠕变变形的速率。
进一步的,考虑模型中的另一个重要影响因素——不同温度下,强化相的尺寸与体积分数对于蠕变速率的影响。
为了更直观的看出各温度下不同强化相尺寸与体积分数的影响,在此以立方体形析出相为例,通过计算蠕变变形率达到5%所用的时间来进行比较,如图9所示。
 (a) 强化相尺寸为500 nm
(a) 强化相尺寸为500 nm (b) 强化相体积分数为70%
(b) 强化相体积分数为70%
Figure 9. Time for creep deformation rate to reach 5%
图9. 蠕变变形率达到5%所用的时间
计算出不同温度下各析出相体积分数与析出相尺寸下的蠕变变形率达到5%所用的时间,将之制作成原图。
由图10可以看出,在更高的温度下,相同的材料蠕变变形率达到5%的时间会更少,即工作温度越高,材料的蠕变性能越差,与实验相符;且在各个温度下,材料的性能变化与之前依然相符,当强化相呈立方体形时,在所选取的强化相体积分数55%~80%内,强化相的体积分数越大,蠕变性能也就越好;在200 nm~800 nm的范围内,高温合金的蠕变性能随强化相尺寸的减小而提高。
 (a) 930˚C
(a) 930˚C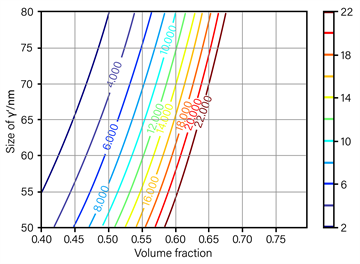 (b) 980˚C
(b) 980˚C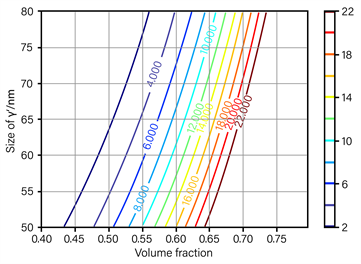 (c) 1030˚C
(c) 1030˚C
Figure 10. Time for creep deformation rate to reach 5% at different temperatures
图10. 不同温度下蠕变变形率达到5%所用的时间
5. 总结
本文针对镍基高温合金“微结构–力学性能”关系,基于高温合金的蠕变变形机制,建立了计及微结构因素的晶体塑性损伤模型,并对模型参数进行了标定,对不同晶相下各
含量和分布的合金进行了蠕变性能的预测。本文所提模型结合热力学计算,动力学计算和第一原理计算,并基于新型镍基高温合金材料的试制和蠕变实验,可以形成计算与实验相结合的镍基单晶高温合金材材料“成分–工艺–组织–性能”的多尺度材料设计方法。
参考文献
NOTES
*通讯作者。