1. 引言
稀疏表示在计算机视觉和模式识别领域有着广泛的应用,目前成为信号处理和机器学习的有力工具。稀疏表示是压缩感知的一个重要环节。压缩感知,是高维空间的低维模型,利用其稀疏低秩的性质,推动了图像处理的发展。而深度学习方法是一个深层高维模型,利用图像的深层特征,对图像进行处理。从结果来看,压缩感知和深度学习都能在像素级别(pixel-level)处理图像的全局信息。同时从方法论这一角度来看,这二者是互补的。压缩感知完全基于模型,有很好的结构,且基于严谨的数学建模。深度学习则完全相反,模型灵活,需要通过数据进行监督学习,是一种基于实证的方法。
大数据的“大”体现在两个方面,量多、维度高。然而数据并不是随机产生的,它们通过结构承载信息。高维数据也不会填满整个空间,由于存在特定的生成机制,其自由度很低。在图像里,这些特点是能被“看”到的:例如对称性、周期性这样的规律在图像的局部和整体都有体现。一张数字图像用矩阵表示,周期性会使这个矩阵的各列线性相关,矩阵的秩肯定比矩阵的规模小很多。也就是说,如果把每一列看成一个向量,看成一个n维空间中的点,当把这些点画出来,会发现它们不是散布得到处都是,而是集中在某一个子空间中,这个子空间就是我们要找的低维结构。这就是高维空间与低维空间的联系。
压缩感知的问题之所以难以解出,正是由于解线性方程时方程数一定要多于未知量,反之求解此类方程则是一个NP-hard问题,因此难以求解。然而常见的高维数据有稀疏的特点,即x不是所有维度都有一个确定值,只有少数非零项的这种情形。大约十年前,陶哲轩和Candès发表了文章,发现这类方程在很宽松的条件下可以用1范数求解 [1]。
解用1范数惩罚过的目标方程(其中对x有稀疏要求),然后进行迭代。将上一次迭代算出的x代入做一个线性变换,得到w,w经过一个软阈值函数后就得到这一次迭代的输出x,重复该过程直到收敛。假设如果我们将这一过程与深度学习相联系,把一次“迭代”建模为一个“隐藏层”,把“阈值函数”设为“激活函数”,便会得到一个类似的简易神经网络。因此,完全从模型推导出来最优的、收敛速度最快的算法,和深度学习通过经验训练得到的神经网络在理论上具有相似性。这些理论也可以被用作图像处理。Hinton最早做的自编码器 [2] 就是这个思路。给定一个数据(Y),如何找到一个一层的线性变换(Q),使得变换后数据(X)最稀疏、维数最低。信号处理就是找到傅里叶变换(FT)或离散余弦变换(DCT)使得数据变得尽可能的可压缩或稀疏。为了验证我们的设想,我们基于稀疏表示的分类网络提出了基于深度稀疏表示的分类网络。
本文的其余部分如下,在第2部分我们介绍了传统的基于稀疏表示的分类网络的相关原理,第3部分描述了基于深度学习的深度稀疏表示的分类网络,第4部分主要包含数据集介绍、实验结果及分析以及相关消融实验,最后,第5部分给出了我们的研究结论、算法存在的不足以及未来的研究方向。
2. 基于稀疏表示的分类网络
基于稀疏表示的分类(SRC)作为稀疏编码的一种应用首次在 [3] 中提出,并证明了其在各种人脸识别数据集上的鲁棒性能。在SRC中,未标记样本被表示为有标记训练样本的稀疏线性组合。这种表示是通过解决一个稀疏性优化问题得到的。一旦找到这一表示,便根据最小重构误差准则给测试样本分配标签。因此SRC方法的基础是找到数据的线性表示。然而,线性表示几乎不足以表示在许多实际应用中出现的具有非线性结构的数据。
在SRC中,给定一组带标签的训练样本,目标是对一组无标记的测试样本进行分类。假设我们已经收集了矩阵
中所有类别为i的向量化训练样本,其中
为每个样本的维数,
为第i类样本的个数,则训练矩阵可构造为:
(1)
其中,
,
,总共有K类。
在SRC中,假设
来自类别i,且一个测试样本
可以很好地由
中某些样本的线性组合来近似。如此,可以通过在训练集中找到一组可以近似
的样本来预测给定的未标记测试样本的类别。从数学模型上讲,这些样本可以通过解决以下优化问题来找到:
(2)
其中,
表示
中非零元素的个数。显然,这一优化问题可以解出这一线性系统的稀疏解。然而,这一问题是一个NP-hard问题,在实际中,稀疏性约束由
的
-范数来实现,这是上述问题的凸松弛情形 [1] [4]。因此,公式(2)在实际使用时变形为以下形式:
(3)
其中,
是一个正项正则化参数。当找到
后,我们可以用下式对
的类别做出预测:
(4)
其中,
是特征函数,用于选择与第i类相关的稀疏系数。例如,假设我们的测试样本是人脸A,其类比为j,当解出
后,就需要用训练样本所构建的字典中A这一人脸的不同角度、不同表情等训练样本来近似稀疏地表示测试样本,即选择了类别为j的稀疏系数,用来表示这一类的测试样本。SRC的方法展示在表1中。

Table 1. Pseudo-code for classification tasks based on sparse representation
表1. 基于稀疏表示的分类任务伪代码
3. 基于深度稀疏表示的分类网络
本文开发了一个基于稀疏表示和深度学习相结合的分类模型。在模型中,训练集和测试集都是可以
观察到的,学习过程期望实现从特定的训练样本到特定的测试样本的推理 [5]。受到Hinton自编码器 [2] 的启发,本文建立了基于卷积自动编码器的方法。网络架构包含一个编码器、一个稀疏编码层和一个解码器。编码器接收训练集和测试集作为原始数据输入,并从中提取深层抽象特征。稀疏编码层通过训练样本的稀疏线性组合重构测试样本,并将它们与训练特征连接起来,然后将其馈送给解码器。解码器将训练嵌入特征和重构的测试嵌入特征映射回数据的原始表示。图1给出了本文的模型架构。输入数据为
,编码器提取的深层特征记为
,稀疏编码层的输出为
,解码器的输出可以看作对输入的稀疏重构,即
。
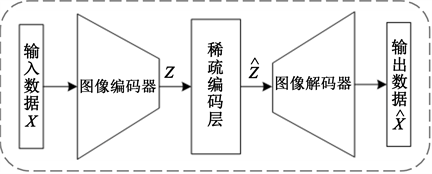
Figure 1. Architecture of classification network model based on deep sparse representation
图1. 基于深度稀疏表示的分类网络模型架构
3.1. 稀疏表示
设
,
分别为给定的向量化后的训练数据和测试数据。将
输送给编码器,输出相应的嵌入特征
,其中
是样本的嵌入特征维度。对于每一个测试样本的最优化问题可以写成嵌入矩阵的优化形式:
(5)
其中A是在列中包含稀疏编码的系数矩阵。
是正的正则化参数。注意,等式(5)中的第一个惩罚项等同于,具有
作为输入、
和A作为输出的可训练参数的神经网络全连接层的惩罚项。因此,考虑到稀疏性约束,可以在具有全连接层的神经网络框架中对优化问题(5)进行建模,该全连接层具有没有非线性激活函数或偏置的稀疏参数。因此本文在稀疏编码层中使用上述这样的模型来为测试样本找到稀疏编码。
稀疏编码层位于编码器和解码器网络之间。它的任务是将
传递给解码器,以及将测试集
的重构特征传递给解码器,即
。假设
是训练特征和测试特征经过稀疏编码层的输出,因此有:
(6)
这里的
是恒等矩阵,表明经过稀疏编码层,训练集特征没有发生改变,仅通过训练集稀疏表示测试集,即测试集的近似重构过程。
若将解码器的输入设为
,则
,其中
(7)
3.2. 网络架构
为了学习图像的视觉特征,我们使用了卷积神经网络,这在表示学习任务 [6] [7] [8] 中展现出了优秀的性能。模型的图像编码器模块由堆栈的卷积层和ReLU激活层组成,解码器由反卷积层和ReLU激活层组成。图2给出了我们的网络细节。稀疏编码层的参数实际上取决于数据集的大小,即n个测试样本、m个训练样本。
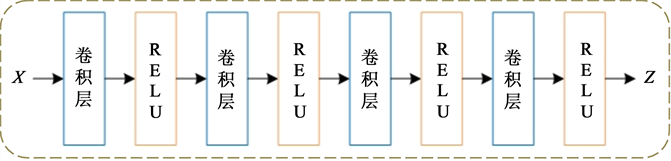 (a)
(a) 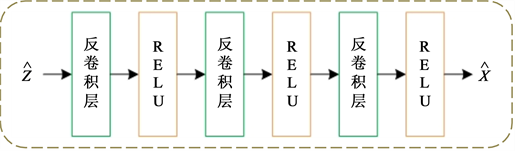 (b)
(b) 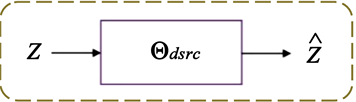 (c)
(c)
Figure 2. Model detail settings. (a) The architecture of image encoder; (b) Image decoder; (c) Sparse encoder layer
图2. 模型细节。(a) 图像编码器架构;(b) 图像解码器架构;(c) 稀疏编码层
3.3. 目标函数
一个包含稀疏编码以及训练编解码器的端到端的目标函数如下:
(8)
其中,
是所有可训练参数的集合,包含编解码器的参数,以及稀疏系数矩阵A。同时,
是解码器的输出,即重构特征,
是正的正则化参数。该目标函数(凸优化问题)同时找到稀疏系数矩阵A和一组适用于提供有效稀疏表示的理想嵌入特征Z。
3.4. 分类任务
一旦找到稀疏系数矩阵A,它就可以将类别标签与测试样本关联起来。对于中的每一个测试样本
,它的嵌入特征是
,并且矩阵A中相对应的稀疏表示列向量是
,将这些用于预测测试集的类别,与公式(4)形式类似,深度稀疏表示用于分类的算法如表2中算法2所示。
(9)

Table 2. Pseudo-code for classification tasks based on deep sparse representation
表2. 基于深度稀疏表示的分类伪代码
4. 实验过程及结果分析
4.1. UMD移动端人脸数据集
实验中使用了UMD移动端人脸识别数据集(UMDAA-01) [9],由于稀疏编码层中的参数数量与训练和测试规模的乘积成比例,故随机选择使用数据集的一个较小的子集,并在选中的子集上进行实验。在实验中,输入图像的大小被调整为32 × 32。该数据集包含50个用户使用智能手机前置摄像头拍摄的750个视频。该数据集是在三个不同的会话中收集的。该数据集最初是为认证任务收集的,但由于其视频帧包括具有不同光照、不同姿态条件以及具有挑战性的面部图像实例,因此它也被用于其他任务 [10] [11]。在这个实验中,我们从会话1的数据中随机抽取每个受试者的50张人脸图像。图3给出了该数据集的图像示例。
4.2. 训练细节
本文使用Tensorflow-1.12.0完成人脸分类任务,同时使用基于动量的自适应梯度下降方法(Adam) [12] 来最小化损失函数,并设置学习速率为10−3。在开始训练目标函数之前,在没有稀疏编码层的数据集上
预训练编码器和解码器。以
为目标对编码解码器进行预训练,其中
表示编码器和解码器
网络中的参数集。在这个阶段,使用的批大小为100。但是在实际的训练阶段,将包括训练样本和测试样本在内的所有样本作为一个大批量的单一样本进行输入。在实验中,将正则化参数设为
和
。

Figure 3. Examples for images in dataset
图3. 数据集图像示例
4.3. 实验结果
本文在传统的SRC以及我们提出的DSRC上,针对同一数据集UMDAA-01做了对比实验,实验结果如表3所示,从表3可以看出,DSRC方法与SRC方法相比有明显的改进。实验结果表明,本文的方法通过结合深度学习的方法对测试集中的人脸图像实现了更好地稀疏重构,通过分析我们的方法不仅可以有效地找到稀疏编码,而且还可以寻找到适合进行稀疏表示的数据(即编码器的输出)。这从一定程度上说明深度学习能够改善传统方法在表示学习任务上带来的缺陷。

Table 3. Performance of the two methods on the task of sparse representation classification
表3. 两种方法在稀疏表示分类上的性能
为了衡量不同的训练样本对于重构测试样本的稀疏表示的性能,我们通过设置不同的数据比例,进行了如表4的消融实验,结果显示了不同训练样本比例下,四个不同版本的分类网络在UMDAA-01数据集上的性能。我们将数据集随机分为训练样本集、测试样本集,分别各占总样本数的20%、40%、60%和80%作为训练样本集,剩余的样本作为测试样本集。当采用训练集与测试集比例为4:1时取得最佳性能,说明训练集的样本数量在一定程度上决定了模型对于测试样本稀疏重构的能力。

Table 4. Influence of the number of training sample on performance of the model DSRC
表4. 训练样本比例对于模型DSRC性能的影响
5. 结论
本文提出了一种基于自编码器的稀疏编码网络。其中引入了一个位于编码器和解码器网络之间的稀疏编码层。该层从编码器接收到深层抽象特征,并重构其稀疏表示。该稀疏表示用于预测测试样本的类别标签。讨论了一个允许端到端训练的模型框架。并且在一个人脸图像分类数据集上的进行的对比实验表明,所提出的网络获得的稀疏表示比传统的SRC方法提供了更好的分类结果。传统的信号处理方式仍然存在一定的优势,如何将其与深度学习方法相结合是我们还需要探索的问题。
基金项目
2022年北京建筑大学研究生创新项目(NO. PG2022145)。
NOTES
*通讯作者。