1. 引言
随着科学与技术的不断发展,热力学与统计物理的研究和应用范围不断扩展,越来越成为科学研究的重要基础知识。《计算物理学》作为现代物理学的一门基础课程,不仅在科学研究中得到广泛的应用,在物理学专业的学生培养中同样愈发重要。
现在学生在学习热力学与统计物理专业课程的时候经常会觉得描述物理理论的数学公式难以理解,很难在脑海中形成相应的物理图像 [1];而在学习计算物理学时又觉得公式繁多,枯燥乏味,感觉在学数学课 [2] [3]。既不知这些知识的用处,更不知该如何使用这些公式解决实际问题。这使学生缺乏运用所学知识解决实际问题的能力。
本文以最简单的混合流体——两种不同元素形成的液体的相行为为研究对象,对此液体系统进行分析、建模,并进行数值求解,最后编写程序通过计算机对两元液体的相行为进行研究。在整个过程中,学生从查找相关资料,通过自主学习了解液体及其相行为,运用所学统计物理知识分析现象,建立物理模型,采用计算物理知识进行数值求解。这使学生既复习巩固所学的热力学与统计物理的知识,又培养运用计算物理知识解决问题的能力。最终达到学而知用,激发学习兴趣的效果。
2. 模型及方法
本文采用耗散粒子动力学作为研究手段。耗散粒子动力学是基于涨落耗散理论的动力学模拟方法 [4] [5]。在此方法中,体系的每个粒子都遵循牛顿动力学:
(1)
为了降低计算量,将每个粒子的质量m设置为1,牛顿方程可表示为:
(2)
其中
为保守力,
为耗散力,
为随机力。耗散力会降低粒子的速度,而随机力则使粒子的速度增加。耗散力和随机力的相互耦合可模拟体系与环境之间的能量交换,最终使体系的温度与环境的达到一致,从而找到体系的平衡态。
通过采用算法对微分方程进行数值求解,可模拟体系从初始状态到平衡态的动力学过程。由于计算机计算量的限制,该模型在空间的三个维度上都采用力周期性边界条件从而可以对宏观体系进行研究。周期性边界条件是通过最小像力约定实现的,即两粒子之间距离在模拟盒子及其镜像中取最小值。
在教学过程中,可以让学生先试着自己建立模型,进行数值求解,编写相关程序。使学生体验计算物理学知识的应用。
3. 模拟结果讨论
在这小节中,将两元素具有较强排斥性的体系的初始状态和平衡态进行对比使学生能够对相及相变概念有更加形象的感性认识;展示两元素排斥较弱体系的热动力学过程,让学生不仅感性地认识热动力学过程,还有助于理解相空间这一概念。仅以温度在热动力学过程中的变化为例,既使学生生动地认识热力学量,还能激发学生探索其他物理量的变化。以激发学习兴趣。
3.1. 体系的相变行为
模型体系的初始状态是通过设定模拟盒子为简单立方盒子,其体积为:
为盒子边长,每种粒子的数目分别为
,体系粒子的总数目为
,每个粒子的坐标为
,速度为
。粒子在模拟盒子中以面心立方排列,但是两种粒子没有产生相分离,其分布呈无序状态(如图1所示)。粒子的初始速度满足麦克斯韦–玻尔兹曼分布。
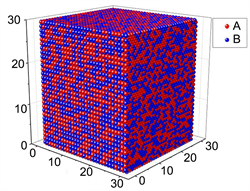
Figure 1. The disordered initial phase of fluid
图1. 液体的初始无序状态
在两种粒子之间排斥相互作用较大时(
),经过一个热动力学过程,液体产生了明显的相分离(如图2所示)。在图2(a)中,我们可以看到两种粒子分成了两个相区。通过单种粒子的相图图片(图2(b)和2(c))可以清晰看出两个相区间的界面是非常平坦的。由于采用了周期边界条件,每个相区都分成两一多一少两个区,但实际上,同种颜色的粒子只组成一个层状相区。
3.2. 热动力学过程
在上面的讨论过程中可以发现溶液体系的相经过热动力学过程后会产生从无序到层状相分离的巨大变化。溶液体系是怎么发生这种从无序到有序转变的问题极大地激发了求知欲。因此我们通过在热动力学过程中的不同点截取体系的过渡状态,探索体系的热动力学过程。图3展示了溶液体系从无序的初始状态通过一系列中间过渡态最后到达稳定平衡状态的热动力学过程。图3(a)是体系的初始状态,其中两种粒子是无序排列的。图3(b)是体系经过100个时间步后的状态,可以看出体系已经发生相分离,但是两相界面还不是很清晰。从图3(c)可以看出,在500个时间步时,两相边界变的稍微清晰了,并且体系状态发生了显著改变。图3(d)是体系的稳定平衡态。从图中可以发现,两相边界非常清晰,体系状态与图3(c)中的差别不是很大。
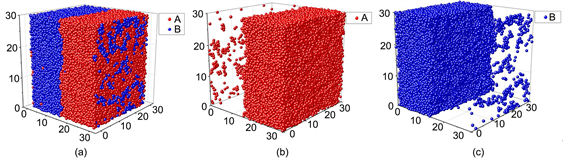
Figure 2. The separated phase of fluid. (a) The phase of fluid composed of two components; (b) The phase domains of A particles; (c) The phase domain of B particles
图2. 液体的相分离平衡态。(a) 体系的状态;(b) A粒子的相区;(c) B粒子的相区
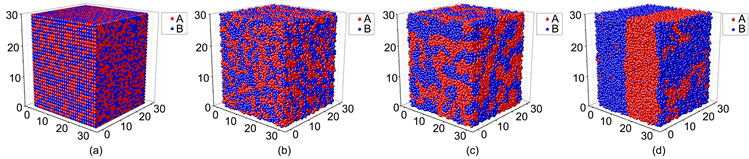
Figure 3. The thermal dynamical process. (a) The initial phase; (b) The phase of s = 100; (c) The phase of s = 500; (d) The terminal phase
图3. 体系在热动力学过程中的状态。(a) 初始状态;(b) 时间步为100时的中间态;(c) 时间步为500时的中间态;(d) 最终的平衡状态
在图3中展示的体系中两种粒子之间的排斥作用为45。与图2中的体系进行比较可以发现两种粒子间的排斥作用强度是影响体系平衡状态的一个重要因素。在教学过程中,建议学生进一步探索体系状态与其他因素间的关系。加深对热力学与统计物理知识的感性认识。
 (a)
(a)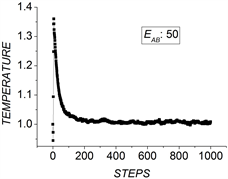 (b)
(b)
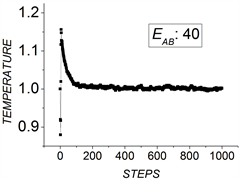
Figure 4. The variation of temperature with time. (a) The system with
; (b) The system with
图4. 温度随时间的变化。(a)
的体系;(b)
的体系
3.3. 体系温度的演化
通过能量均分定理可以计算体系在任一时间步的温度,从而能够给出体系温度随时间的变化。本文主要考察了上述两个体系的温度变化。图4(a)是两种粒子间相互排斥作用值为40的体系的温度随时间的变化。体系温度首先会从标定环境温度急剧下降,然后上升,接着降到环境温度附近并在其上下涨落。图4(b)展示两种粒子间相互排斥作用值为50的体系的温度随时间的变化与相互作用为40的体系的温度相似。不同的是温度下降减少,升高明显变大。
在教学过程中,可以鼓励学生计算其他的物理量,例如体系的动能、势能、内能、热容、压强等。以巩固和加深对热力学与统计物理的知识的理解。
4. 结论
本文以两种元素组成的液体的相行为为例进行教学设计,意在使学生对此物理现象进行分析、构建模型、并进行数值求解和编写程序,可视化液体的相及相随时间的演化,进而形象地了解体系的热动力学过程。这种教学模式可使学生加深对理论知识的理解和应用,以降低学习难度,激发学习兴趣,培养学生运用所学知识解决问题的能力。
基金项目
新疆大学物理科学与技术学院教育教学改革项目。