1. 引言
伴随着矿山开采技术向着高效化与精细化的发展,不可避免地是设备产尘量的增加,经过破碎细化后的矿石会在生产运输过程中产生大量粉尘,对业内人士的身体健康造成极大影响。因此,针对日益严峻的粉尘污染问题,本文选择了一款矿山防尘装置,并对其传动轴进行了进一步的分析与优化,为抑制矿山防尘装置整体振动和传动轴变形提供了理论依据。
传动轴作为矿山防尘装置中的重要部件,作用是将动力传递给提升机构。在装置运行过程中,传动轴结构的细微变化都将会直接引起一系列的稳定性及安全性问题,因此在实际作业中对于传动轴的精度、刚度以及抵抗受迫振动的能力等方面有着较高要求 [1]。
针对此课题,国内外在传动轴动态性能的分析与优化等领域做了许多研究。H G Sanchez [2] 等提出一种基于运行模态分析(OMA)的非参数技术“Peak pick”,能够确定传动轴旋转状态下模态参数。Sivakumar C [3] 通过模态分析确定了由复合材料所制成传动轴的模态参数,验证了金属复合材料取代传统传动轴的可行性。Kim W [4] 等利用不同的壳理论对传动轴的模态和弯曲固有频率进行了分析。丁国平 [5] 等以汽车传动轴为基础,设计了CFRP传动轴的铺层方案,验证了传递矩阵法对一阶模态分析的准确性。余凯 [6] 等设计了一种化工机械传动轴动态特性补偿算法,能够实现传动轴的动态特性补偿。
本文采用ANSYS Workbench有限元分析软件对传动轴进行约束模态分析,得出其在约束条件下的固有频率、振型、变形情况。通过约束模态分析反映出传动轴实际工作状态,为其后续的优化设计、判断其动态性能指标以及检验现结构稳定性提供理论依据 [7]。
2. 矿山防尘装置工作原理
矿山防尘装置由电机提供动力,经过蜗轮蜗杆减速箱后将动力传递给传动轴。传动轴上连接锥齿轮,通过啮合的锥齿轮改变动力方向,将动力传递给链轮。最后由链轮传动与开式链啮合控制防尘罩的升降,使得物料在下落时被限制在防尘罩内,从而限制粉尘的逸散对人和机械的影响。而其中传动轴是整个矿山防尘装置不可缺少的重要组成部分,本文以下内容将对传动轴进行具体的分析。矿山防尘装置实物如图1所示。矿山防尘装置运动简图如图2所示。

Figure 1. Physical picture of mine dustproof device
图1. 矿山防尘装置实物图
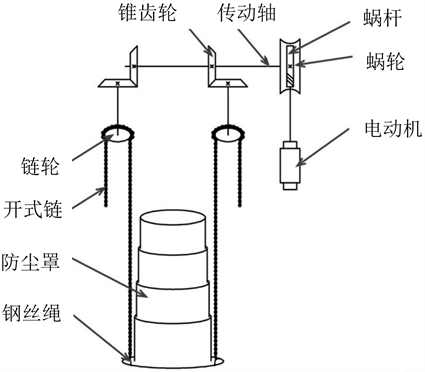
Figure 2. Movement diagram of mine dustproof device
图2. 矿山防尘装置运动简图
3. 模态理论
模态分析是计算结构振动特性的方法,将振动系统中互相耦合的运动方程通过模态坐标变换,使方程组解耦,进而求出各阶模态参数。由于固有模态与外力无关,结构阻尼对固有频率的影响微乎其微,因此可以忽略外力和阻尼,即无阻尼模态分析。
此时运动方程为:
(1)
式中:
是质量矩阵;
是阻尼矩阵;
是刚度矩阵;
是位移矢量;
是速度矢量;
是加速度矢量。
结构的自由振动为简谐振动,将简谐振动方程代入运动方程式(1),得:
(2)
在自由振动时,广义物体结构中的固有频率是必然存在的,即式(2)必然有非零解,因此可得自由振动频率方程:
(3)
取
为特征值,令
,可将式(3)写成:
(4)
假设有
个节点,将式(4)展开:
(5)
若结构刚度矩阵
和质量矩阵都是
阶方阵,解式(5)可得
个广义特征值
,从而求得
个固有频率
,对于每个固有频率
,由式(2)可以确定一个由
个节点振幅构成的列向量,即振型 [8]。
4. 模态分析
4.1. 建立三维模型
有限元仿真的分析效率与准确性受模型影响较大。首先使用SolidWorks软件对传动机构按照实际尺寸进行三维整体建模,如图3所示,传动轴轴径最大处轴段两侧安装轴承进行固定,通过键槽与锥齿轮连接传递动力,轴径最小处轴段与联轴器配合。本文主要考虑传动轴振动特性的影响,提取出传动轴的三维模型,如图4所示。
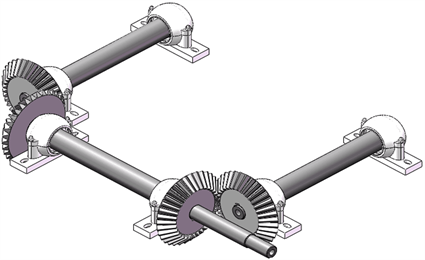
Figure 3. 3D geometric model of transmission mechanism
图3. 传动机构的三维几何模型
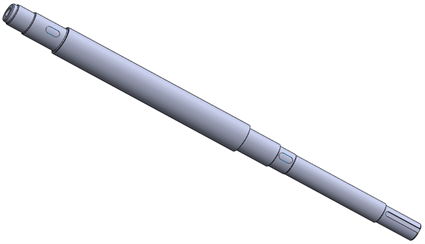
Figure 4. 3D geometric model of the drive shaft
图4. 传动轴的三维几何模型
将三维模型导入Workbench后,需要先对传动轴的材料属性进行定义,传动轴材料选用40Cr,材料具体属性参数如表1所示。

Table 1. Drive shaft material properties and parameters
表1. 传动轴材料属性与参数
4.2. 传动轴的有限元模型
在进行模态分析时,单元网格的质量会直接影响到后续计算的精度,考虑到键槽、小倒角、轴肩等微小特征尺寸在有限元网格划分中的准确性,本文采用四面体法进行网格划分。这种方法自适应性强、易自动生成且能够兼顾时效与计算精度。将整体单元大小设置为3 mm,对键槽与轴肩圆弧部分进行了优化处理 [9]。共生成节点755,973个,单元525,273个。传动轴的有限元模型如图5所示。

Figure 5. Finite element model of drive shaft
图5. 传动轴的有限元模型
4.3. 约束模态分析
约束模态分析指模拟结构的实际工作状态对其进行模态分析。故需要对结构施加实际工况下的约束和载荷,以此保证结果的准确性。在考虑实际工作状态条件下,按照图3所示结构添加约束载荷:1) 在轴径最大处轴段两侧轴肩添加位移约束,对X、Z方向约束。2) 在与轴承座连接处添加圆柱形支撑,固定径向与轴向。3) 在左端与锥齿轮连接处添加力载荷
,在右端与锥齿轮连接处添加力载荷
。
模态分析是研究结构动力特性的一种方法,使用时需要着重考虑传动机构在工作条件下所涉及到的频率。低阶固有频率与振型对传功机构的影响比高阶要大。如若将结构的所有固有频率及振型都进行求解,不仅会增加分析工作量,而且实际意义不大 [10]。因此本文只考虑低阶模态。在ANSYS Workbench中通过Static Structural-Modal耦合模块对传动轴进行约束模态分析,求解出传动轴前6阶模态,计算结果如表2所示。

Table 2. Calculation results of constrained mode analysis of drive shaft
表2. 传动轴约束模态分析的计算结果
5. 稳定性研究分析
提取出约束模态下传动轴前6阶振型,并对其进行稳定性研究分析。振型如图6所示。
结合表2与图6可知,传动轴前6阶的固有频率散布在473.53~2239.4 Hz之间,振型以弯曲变形为主 [11]。一阶振型最大变形在传动轴右端联轴器处,为32.198 mm;二阶振型为径向膨胀,最大变形在轴径最大轴段,为13.922 mm;三阶与四阶固有频率基本相等,振型为以Z向为主和以Y向为主的弯曲变形,最大变形皆为轴径最大处轴段的中部,因此可视为重根;五阶振型最大变形在轴径最小处轴段的中部,为27.912 mm;六阶振型最大变形在传动轴右端联轴器处,为30.816 mm [12]。
结合以上内容,本文选择变形量最大三点进行研究,分别为一、五、六阶模态中的对应变形量为32.198 mm、27.912 mm、30.816 mm三处。通过研究可以看出,3个点均位于传动轴轴径最小轴段,其中有2个点属于高频区域。轴径最小处轴段在实际中与一级减速器连接,负责传动机构中的动力输入。在一般工作状态下,电机的激励频率在30 Hz左右,与传动轴的固有频率相差较大,很难引起共振。但是在矿山作业中会产生噪音等其他外界激励,如果这些外界激励频率与传动轴的一、五、六阶模态的频率接近可能会引起共振,造成传动轴寿命降低甚至被破坏等问题 [13]。因此,轴径最小轴段可作为优化设计的部位,通过改善结构、改变质量等方式减弱振动。
6. 结语
本文以矿山防尘装置的传动轴为研究对象,通过SolidWorks软件对传动轴进行三维建模,在Workbench中划分网格,运用Static Structural-Modal耦合模块对传动轴进行模态分析,得出传动轴的固有频率、振型以及变形情况。
通过模态分析反映出传动轴的振动特性,经过求解得出传动轴的固有频率分布在473.53~2239.4 Hz之间,变形量分布在13.922~32.198 mm,确定了在振动过程中传动轴的主要变形形式是弯曲变形。根据矿山防尘装置在运输作业中的实际工况针对传动轴的稳定性作出研究分析,为后续结构优化、提高结构性能提供了理论依据。
基金项目
国家级大学生创新创业训练计划项目:矿山粉尘自动化处理设备(编号:202111488034)。