1. 引言
超高压装置是超高压技术的重要组成部分 [1],在射流切割、晶体增殖和粉末冶金等设备制造中需要使用超高压技术 [2] [3],且超高压装置在人造金刚石技术中也发挥着关键作用 [4],预应力结构模具是通过在工作开始前预先对模具施加一定载荷,使模具产生反向的预紧力,能够增加模具的承载能力 [5]。缠绕预应力结构是一类具有特殊结构的模具,通过将高强度钢丝或钢丝缠绕在压缸上对压缸施加预紧载荷,改变钢丝或钢丝的张力来调节压缸的预应力大小,使模具预应力分布更好 [6]。在工作压力等条件相同时,缠绕预应力结构 [7] 比年轮式结构更加紧凑,在尺寸等条件相同时,缠绕预应力结构比年轮式结构承载能力更好。预应力缠绕技术具有结构紧凑、承载能力好、加工方法简单等特点,在诸多领域得到应用。预应力缠绕模具的关键技术是对缠绕张力的研究 [8] [9],国外对预应力缠绕技术 [10] 的研究主要分布在丹麦科技大学和丹佛斯公司等单位,经过发展与完善,已经用于工业生产,但是出于对自身利益的保护,相关文献或技术很少公开;国内对预应力缠绕技术的研究主要集中在与缠绕相关的工业领域中,针对模具缠绕的深入研究较少 [11]。
本文对钢丝张力调节部分中钢丝轴向应力变化进行分析,对钢丝张力的产生进行力学模型分析,通过有限元仿真研究分析在不同影响因素(液压缸压力、钢丝速度、钢丝直径)下,钢丝的轴向应力变化,以解决缠绕过程中钢丝所受的轴向应力超过钢丝的抗拉强度时易发生断裂,形成安全隐患。
2. 钢丝张力调节机构原理
2.1. 张力调节机构结构
变张力钢丝缠绕装置的关键就是对钢丝的张力进行控制,张力调节机构的轴测图如图1所示。张力调节机构主要由液压缸、导柱、上下垫块、上下压块等组成。下垫块通过螺钉固定安装在液压机底座上,上垫块与液压机中活塞杆末端相连,上垫块通过导柱可上下调节位置,在上下垫块上各自安装一个压块,两个压块之间钢丝从中穿过上加工出半径略小于钢丝直径的凹槽,且两端入口处加工为喇叭形,可以方便钢丝穿过。在缠绕工作开始前,将钢丝穿过上下镶块。液压系统与PLC相连,在缠绕工作过程中,张力检测机构不断检测钢丝张力值并反馈给PLC,PLC通过对比检测值与理论预定值,分析计算出张力补偿量,控制液压系统来及时调整液压缸的油压,从而调整钢丝张力值,使其满足预设要求。
2.2. 钢丝受力分析
当钢丝两端被拉紧时,由于其钢丝本身内力的存在,在钢丝上就会产生一个抵制变形的力,通常这个力,我们称作张力。当钢丝被两端拉紧时所产生的应力与钢丝张力两者之间的关系:
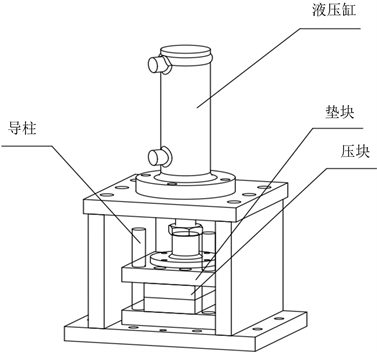
Figure 1. Axonometric drawing of the tension adjustment mechanism
图1. 张力调节机构轴测图
(1)
式中:T为钢丝张力,A为钢丝的横截面积,
为钢丝横截面积上产生的拉应力。
钢丝张力的大小主要是通过液压系统对其进行调节,在张力调节机构中,钢丝处于上下两个垫块之间,此时液压缸通过上下两个垫块来对钢丝施加与钢丝轴向相垂直的压力,由于各个部件之间存在摩擦,且钢丝张力主要就是通过钢丝与上下两个垫块之间的摩擦力提供,钢丝与其余部件之间的摩擦力可忽略不计,张力调节机构中钢丝张力产生的情况可简化为图2所示。
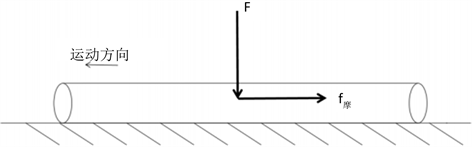
Figure 2. Brief diagram of the force of the wire
图2. 钢丝受力简图
钢丝张力的表达式为:
(2)
摩擦力
:
(3)
(4)
式中:μ为钢丝与两垫块之间的摩擦系数,
为钢丝许用应力,d为钢丝直径。
从上式中可以得出,钢丝张力受液压缸压力与钢丝横截面积有关。而且本装置是用于超高压模具上的钢丝缠绕装置,由于钢丝缠绕过程,钢丝的张力会随时发生变化,随着钢丝层厚度的增加,钢丝张力也在不断变化,因此需要伺服电机通过对输入控制电压信号来直接调节模具的转速,实现通过控制钢丝缠绕速度,来精确且及时的对钢丝变张力控制信号进行调节。因此钢丝的缠绕速度也会对钢丝张力产生影响。
钢丝张力由液压缸提供,液压系统供油压力的平衡方程为:
(5)
(6)
式中:A为液压缸的有效工作面积,Ps为液压缸工作压力,D为液压缸缸径。
3. 钢丝张力调节机构的有限元模型
为了研究钢丝张力与钢丝直径、压缸压力以及钢丝缠绕速度之间的关系,采用ANSYS LS-DYNA模块建立钢丝张力调节机构的有限元模型,考虑到由于钢丝张力的产生只发生在钢丝与上下两垫块之间,为了减少计算量,仅对该部分进行有限元建模,且不会影响到仿真结果的准确性,如图3所示。

Figure 3. Brief diagram of the finite element model of the wire tension adjustment mechanism
图3. 钢丝张力调节机构有限元模型简图
上下两垫块定义为Solid186实体单元,钢丝定义为Beam198结构钢单元,网格划分采用MultiZone多域扫掠型算法,划分网格单元尺寸为1 mm。依照实验参数确定有限元仿真模型的数值,钢丝的材料选择为Q235结构钢,材料的主要性能有杨氏模量为200 GPa,密度为7850 kg/m3,泊松比为0.3,屈服强度为235 MPa,抗拉强度为400 MPa。
为了更好地定义钢丝的速度,把钢丝分为两部分,其中一部分设置在与垫块末端相距一定距离的位置,这样就可以通过设置钢丝通过垫块末端的结束时间来设定钢丝速度,如图4所示。把一段钢丝设置在与垫块末端相距10 mm处,通过设置钢丝通过垫块末端的结束时间为1 s,则钢丝的缠绕速度则为10 mm/s。这样就可以通过设置结束时间的长短,来到达钢丝速度的改变。把两部分钢丝之间定义为绑定约束,由于钢丝张力就是因为钢丝与垫块之间的摩擦产生,所以定义钢丝与垫块之间为摩擦约束,摩擦系数为0.15。通过LS-DYNA中的显式动力学分析方法,研究钢丝在不同条件下轴向应力的变化。
针对研究目标,设计如下几种情况:钢丝直径为3、4和5 mm,液压缸压力分别设定为500 N、1000 N和1500 N,钢丝速度分别设定为10、25和40 mm/s。经过数值模拟后,对钢丝在不同条件下的轴向应力进行对比分析。
4. 仿真结果分析
对液压缸预紧的钢丝受到不同压力和不同速度的作用下,钢丝的轴向应力都会出现相应的变化。为研究钢丝轴向应力的变化规律,分别取不同压力与速度的钢丝,将数值模拟结果与文献 [12] 的理论结果进行对比,图5为钢丝直径取5 mm时,不同压力下的钢丝轴向应力–速度曲线,如图5所示。从图中可以看出:钢丝的轴向应力随着钢丝速度的增加,轴向应力先逐渐增大,然后达到峰值,随后随着速度的增加,轴向应力开始减小,这是由于钢丝随着速度的增加,而钢丝张力就是通过钢丝与垫块之间的摩擦而产生,随着速度的增加,钢丝与垫块之间的温度不断升高,导致钢丝与垫块摩擦系数降低,从而摩擦
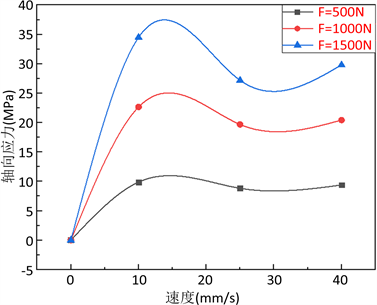
Figure 5. Axial stress-velocity curves of steel wires at three different pressures
图5. 三种不同压力下的钢丝轴向应力–速度曲线
 d = 4 mm d = 3 mm
d = 4 mm d = 3 mm
Figure 6. Axial stress-velocity curves of steel wires of different diameters
图6. 不同直径的钢丝轴向应力–速度曲线
力即钢丝张力减小。而后钢丝轴向应力又开始相对增大,但增长的幅度很小,并逐渐趋于平稳。从图中还可以看出液压缸压力越大,钢丝轴向应力越大,该数值模拟结果与理论计算结果相符合,钢丝轴向应力与液压缸压力成正相关。结合仿真结果分析,在钢丝直径与所受液压缸压力相同时,钢丝缠绕速度在10 mm/s左右时,钢丝轴向应力达到峰值,由于本装置是用于超高压模具上的钢丝缠绕,所需要的钢丝张力较大,且经过与钢丝材料的性质进行对比,不超过钢丝的屈服极限与抗拉强度,不会出现钢丝断裂的情况。
为进一步研究钢丝轴向应力与钢丝直径之间的变化规律,分别取不同直径的钢丝,如图6所示,图6为钢丝直径取3 mm和4 mm时钢丝轴向应力–速度曲线图。通过图5与图6对比可以看出:随着钢丝直径的增大,数值模拟结果与理论计算结果比较接近,在液压缸压力和钢丝速度相同的条件下,钢丝直径越大,钢丝轴向应力越小,也更进一步证明了钢丝轴向应力与钢丝直径呈线性相关。
5. 结论
1) 提出了一种新型的钢丝张力调节机构,这种调节机构可以有效且精准地控制钢丝张力大小,可以避免在缠绕过程中钢丝所受的轴向应力超过钢丝的抗拉强度时易发生断裂的问题,不会形成安全隐患。
2) 建立了钢丝张力调节机构有限元模型,数值模拟结果表明:当钢丝直径相同时,承受相同的压力下,随着钢丝速度的增加,钢丝轴向应力先增大,达到峰值,而后减小并最终趋于平稳;当钢丝速度一定时,钢丝轴向应力与压力成正相关。
3) 随着钢丝直径的增大,在液压缸压力和钢丝速度相同的条件下,钢丝直径越大,钢丝轴向应力越小,钢丝轴向应力与钢丝直径呈线性相关。