DOI: 10.12677/SA.2022.113067, PDF, , ,  被引量    国家社会科学基金支持
作者: 傅嘉琪, 吴杭亮, 周昌隆, 朱 莉：宁波工程学院，浙江 宁波
关键词: ARIMA模型；LSTM模型；混合模型；股票短期预测；ARIMA； LSTM； Hybrid Model； Stock Short-Term Prediction

文章引用：傅嘉琪, 吴杭亮, 周昌隆, 朱莉. 基于ARIMA-LSTM混合模型的股票短期预测[J]. 统计学与应用, 2022, 11(3): 630-637. https://doi.org/10.12677/SA.2022.113067

1. 引言

股市如今已成为中国经济发展不可或缺的重要组成部分。由于股市的高回报率，其始终是备受欢迎的投资之一，而股票价格预测也成为商业领域的热点问题。如何对股票价格时间序列进行准确的预测，对金融投资决策与风险管理具有特别重要的意义。然而股票价格取决于诸多因素的影响，这使得股票价格预测较为复杂。根据模型构建的不同理论，股票价格预测模型主要分为两类，一类是基于统计理论的传统统计模型，例如传统时间序列模型、隐马尔可夫模型等；另一类是基于机器学习、深度学习的创新型模型，例如基于支持向量机的预测模型、基于决策树的创新模型、基于神经网络的创新模型等新型股票预测方法。

在对股票数据的研究中，有许多的研究学者曾利用单一的传统时间序列模型或单一的神经网络模型对股票价格进行预测：吴玉霞等 [1] 运用ARIMA模型对股票价格进行预测；齐天铧 [2] 基于灰色模型与ARIMA模型对股票价格进行预测；黄超斌等 [3] 则运用长短期记忆神经网络模型对上证综合指数进行预测，证实了长短期记忆神经模型在金融时间序列数据上的预测效果。

单一的模型只能够提取复杂数据中的线性或非线性其中一种关系。本文提出一种结合线性和非线性模型特点、对数据进行识别处理、实现对数据线性关系和非线性的全部描述以达到提高预测结果准确性的混合模型，即构建传统时间序列及长短记忆神经网络混合模型(ARIMA-LSTM混合模型)。利用混合模型对拓普集团股票价格进行预测，并将其预测结果与单一的传统时间序列模型ARIMA的预测结果进行对比分析。

2. 模型介绍

2.1. ARIMA模型

ARIMA (Autoregressive Integrated Moving Average)模型，全称为差分整合移动平均自回归模型，是一种由Box和Jenkins提出的对时间序列数据进行分析和预测比较完善和精确的算法模型 [4]。ARIMA模型预测原理可简括为：模型将时间序列数据默认为一组随机序列，使非平稳的数据经过差分后趋于平稳，转换为平稳的时间序列，并对以往数据间的线性关系构建模型，以预测数据未来值。

ARIMA模型的建模流程主要分为以下几个步骤：首先是ARIMA模型自回归部分，它用于特定的数据点对当前数据点进行回归，前期的数据点称为滞后点，并由p表示进行回归所需的滞后点数量。其次计算差异度q，利用ARIMA模型中的积分因子算出当前观测数据和以往滞后观测数据的差异总值。最后得出差分阶数d，这是于前期计算基础上利用平均因子计算移动平均模型用于滞后观测的回归误差。即ARIMA (p, d, q)中，AR是“自回归”，p为自回归项数；MA为“滑动平均”，q为滑动平均项数，d为使之成为平稳序列所做的差分次数(阶数)。此模型通过调节三个参数d、p、q可对预测结果进行调整，从而达到最优 [5]。ARIMA模型中，观测变量的预测值假定为过去几个观测值和随机误差的线性函数，模型计算公式可表示为：

$y_t={\theta }_0+{\varphi }_1{y}_{t-1}+{\varphi }_2{y}_{t-2}+\cdots +{\varphi }_p{y}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-{\theta }_2{\epsilon }_{t-2}-\cdots -{\theta }_q{\epsilon }_{t-q}$ (1)

其中 $y_t$ 和 ${\epsilon }_t$ 分别是时间段t的实际值和随机误差； ${\varphi }_i\left(i=1,2,\cdots ,p\right)$ 和 ${\theta }_j\left(j=1,2,\cdots ,q\right)$ 是模型参数；p、q也是上文提到过的模型参数，其含义为模型的阶数(p、q均为整数)；随机误差 ${\epsilon }_t$，在模型中假定是独立且服从相同的分布，其均值为0；常数项方差记为 ${\sigma }^2$。式(1)涉及ARIMA 系列模型的几个重要特殊情况。如果q = 0，则可简化为p阶的AR模型。当p = 0时，模型可简化为q阶MA模型。其中，模型阶数(p, q)是ARIMA模型构建的关键环节，其决定了模型预测的准确性。

2.2. LSTM神经网络模型

神经网络对于处理非线性数据具有很强能力。神经网络的特点是参数维数大、通用性强，并且其在每一层中使用非线性激活函数，因此使该模型能够在非线性数据下有很好适应处理能力 [6]。长短时记忆网络(Long Short Term Memory Network, LSTM)是由循环神经网络(Recurrent Neural Networks, RNN)延伸发展而来，在普通RNN基础上，在隐藏层各神经单元中增加及一单元，从而使RNN具备了长期的记忆功能。本文介绍的具有遗忘门的标准LSTM单元由四个交互神经网络组成，分别代表遗忘门、输入门、输入候选门和输出门。遗忘门输出一个向量，其元素值介于0和1之间。它充当一个遗忘器，该输出向量乘以前一个时间步的细胞状态 $c_{t-1}$，以删除不需要的值并保留预测所需的值。如下图1给出LSTM神经网络存储细胞内部结构。

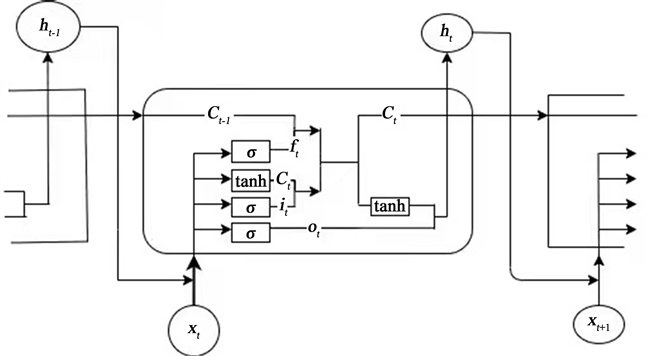
Graph 1. Internal structure of LSTM neural network storage cell

图1. LSTM神经网络存储细胞内部结构

在下一阶段中，输入门和输入候选门共同作用以生成新的单元状态 $C_t$，该状态将作为更新的单元状态传递到下一单元。输入门使用sigmoid函数作为激活函数，输入候选门则选择tanh函数为激活函数，并输出 $i_t$ 和 ${\tilde{C}}_t$。 $i_t$ 用以选择 $C_t$ 中的哪个特征应反映到新的单元状态 ${\tilde{C}}_t$ 中。

$\sigma \left(X\right)=\frac{i}{1+{\text{e}}^{-X}}$ (2)

$i_t=\sigma \left(W_i\times \left[h_{t-1},x_t\right]+b_i\right)$ (3)

${\tilde{C}}_t=\tanh \left(W_c\times \left[h_{t-1},x_t\right]+b_c\right)$ (4)

tanh函数，是双曲正切函数。与sigmoid函数不同的是，sigmoid函数输出值介于0和1之间的值，而tanh输出则介于−1和1之间。最终将 $O_t$ 经tanh激活后的单元状态与 $C_t$ 组合为输出门 $h_t$。最后更新的单元状态 $C_t$ 是应用了遗忘门的先前单元状态 $C_{t-1}$ 和更新后的tanh函数激活的单元状态 ${\tilde{C}}_t$ 的组合。

${\sigma }_t=\sigma \left(W_o\times \left[h_{t-1},x_t\right]+b_o\right)$ (5)

$C_t=f_t\times C_{t-1}+i_t\times {\tilde{C}}_t$ (6)

$h_t=o_t\times \tanh \left(C_t\right)$ (7)

由式(6)和(7)所得的细胞状态 $C_t$ 和输出 $h_t$ 将被传递到下一个时间步骤，并将经历相同的过程。根据任务的不同，进一步使用合适的激活函数，如Softmax激活函数或双曲正切tanh激活函数均可用于激活输出门 $h_t$。在本文实验中，这是一个输出值在−1和1之间的回归任务，因此选择tanh函数来激活数据向量X最后一个元素的输出更为合适。

2.3. ARIMA-LSTM混合预测模型

考虑到ARIMA模型只局限于预测数据的线性部分，而LSTM神经网络模型更适合对数据的非线性部分信息进行提取，因此我们提出一种能够提取数据线性及非线性特点的ARIMA-LSTM混合模型对复杂的股票数据进行拟合。混合模型的思想是：通过ARIMA模型建模提取股票数据存在的线性关系，充分利用时间序列上数据间的关联性；根据自回归差分平均模型可知残差序列理应不呈现线性相关，因此进一步利用LSTM神经网络模型训练修正残差序列，再将修正后的残差序列作为输出。最终结合ARIMA模型预测的线性部分和LSTM模型对残差的修正得到最终的股票预测值。

在进行混合模型中提取数据线性关系时与一般的ARIMA建模步骤相同；在训练残差时，利用LSTM模型实现残差预测属于监督机器学习算法，损失函数选择均方误差损失函数MSE，在接近收敛点处时，梯度会慢慢变小，避免陷入局部最小值，有利于得到更精确的结果。计算公式为：

$L\left(y,f\left(x\right)\right)=\frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-f\left(x_i\right)\right)}^2}}{n}$ (8)

式(8)中， $L(\cdot )$ 为MSE损失值， $y_i$ 为样本期望值， $f\left(x_i\right)$ 为样本预测值。

模型训练中，优化器在很大程度上影响模型运行的速度。根据损失函数计算的误差信号，通过优化算法更新连接权值。Adam是一种计算每个参数的自适应学习速率的方法，克服了传统梯度下降法可能会收敛到局部最优的问题。本文通过算法Adam更新连接权值矩阵，实现各参数学习率的自动调整，对LSTM网络权重参数进行更新，对网络进行迭代训练，加快算法收敛速度，提升效率。公式如下：

$m_t={\beta }_1{m}_{t-1}+\left(1-{\beta }_1\right)\frac{\partial L}{\partial \theta }$ (9)

$v_t={\beta }_2{v}_{t-1}+\left(1-{\beta }_2\right){\left(\frac{\partial L}{\partial \theta }\right)}^2$ (10)

式中， $m_t$ 梯度一阶矩估计； ${\beta }_1$ 为超参数，一般取0.9； $v_t$ 为梯度二阶矩估计； ${\beta }_2$ 为超参数，一般取0.999做如下的偏差修正，使得参数可以正常更新：

${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t}$ (11)

${\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$ (12)

式中， ${\hat{m}}_t$ 和 ${\hat{v}}_t$ 分别为修正的梯度一阶估计值和二阶估计值。

Adam算法更新参数的公式如下：

${\theta }_{t+1}={\theta }_t-\alpha \frac{{\hat{m}}_t}{\sqrt{{\hat{v}}_t+\epsilon }}$ (13)

式中， $\alpha$ 为神经网络模型的学习率； $\epsilon$ 为防止除零误差常数，取为10⁻⁸。

3. 实证分析

3.1. 数据选取

本文的实验数据为2015年3月19日至2022年3月31日的拓普集团股票历史交易数据，选取的有效数据共计1705条，将数据分为训练集与测试集两个部分，且前1685条数据为训练集数据，最后20条为测试集数据。利用R软件绘制出训练集数据的时序图如图2左，直观判断原序列不具平稳性；绘制数据一阶差分图如图2右，进一步判断数据不具方差齐性。

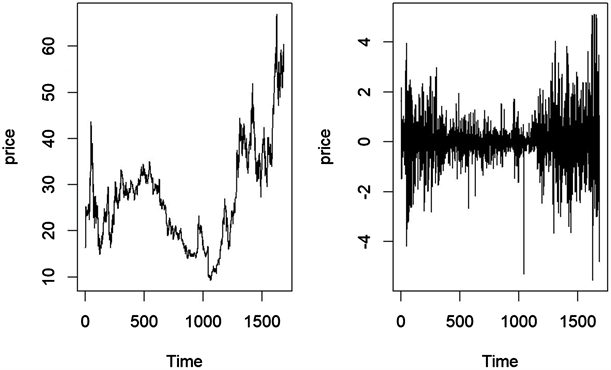
Graph 2. Time series and first-order difference of stock data of Tuopu Group

图2. 拓普集团股票数据时序图及一阶差分图

3.2. ARIMA模型拟合与预测

对非平稳的股票序列进行一阶差分后的序列进行平稳性检验及白噪声检验，得到一阶差分后的序列为平稳非白噪声序列，根据一阶差分后序列的自相关和偏自相关图我们选取可能的ARIMA模型进行参数显著性、模型显著性检验并根据赤池信息准则，筛选出针对拓普集团股票数据的最优传统时间序列模型——ARIMA (3, 1, 2)。在实验中选取的各ARIMA模型检验结果及AIC如下表1。

通过ARIMA的一般建模步骤得到该只股票预测下的最佳ARIMA模型：ARIMA (3, 1, 2)，并得到如下ARIMA拟合预测图。图3中蓝色线代表数据原始值，黄色线代表ARIMA (3, 1, 2)模型的拟合预测线。前1685个数据为ARIMA (3, 1, 2)模型的拟合部分，拟合结果与原数据高度重合；最后二十个数据为预测数据，但是预测部分存在较为明显的误差，这说明单一的ARIMA模型对股票数据进行拟合预测极易过拟合从而使得预测出现较大偏差。

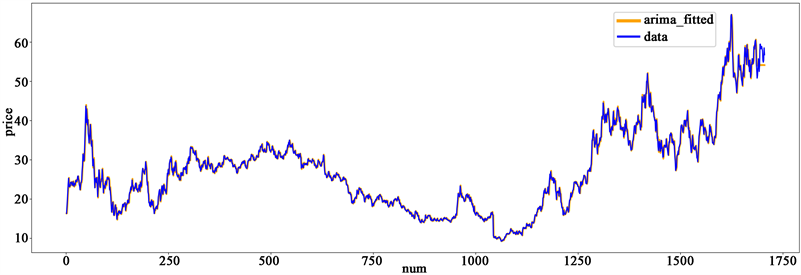
Graph 3. ARIMA fitting and prediction results

图3. ARIMA拟合预测结果

3.3. 混合模型拟合与预测

利用python语言建立混合模型中LSTM神经网络模型部分，利用ARIMA模型的拟合数据与原数据所产生的残差序列作为训练集数据进行LSTM神经网络模型训练，以此来达到混合模型中非线性部分的调整。在实际操作中通过多次调整LSTM神经网络模型参数，进行大量的对比实验来优化模型预测效果。当参数调整至中间神经元个数为64个，学习率为0.005进行的迭代次数为50次，得到最优的残序列LSTM模型。进一步将参数优化后的LSTM模型对残差进行二十步预测，并结合ARIMA模型二十步预测中的线性部分，得到最终的混合预测结果如下图4。

3.4. 模型比较

根据最后20个股票数据的预测结果(见表2)进一步计算并比较两个预测模型的平方绝对误差(MAE)、均方误差(MSE)及平均绝对百分比误差(MAPE)得到表3。三类误差均是误差数值越小表示模型预测效果越好，根据表中结果可直观地看到三类误差均显示混合模型的预测结果要优于传统的ARIMA模型。可见在针对拓普集团的股票数据进行预测时，ARIMA与LSTM搭建的混合模型的预测效果要优于单一的ARIMA模型。

3.5. 模型验证

利用所建立的ARIMA-LSTM模型对其他股票进行预测分析，从而验证模型泛化效果。选取的数据为2017年1月9日至2022年4月22日的太平鸟股票历史收盘价，其中有效数据共1282条。将数据分

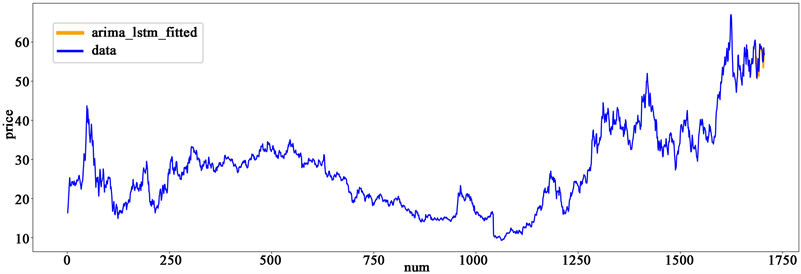
Graph 4. ARIMA-LSTM prediction results

图4. ARIMA-LSTM预测结果

为训练集与测试集两个部分，且前1262条数据为训练集数据，最后20条为测试集数据。预测结果及预测误差如下表4、表5。预测结果和预测误差均显示所建立的ARIMA-LSTM模型具有较高的预测精度，这说明模型具有较好的泛化能力。

4. 结语

本文选取了拓普集团股票的1705条数据，分别构造了ARIMA模型与ARIMA-LSTM混合模型，并对股票数据进行短期预测。针对构造的ARIMA-LSTM混合模型中神经网络模型部分，通过多次调整模

型参数进行大量对比实验来优化模型预测效果。实验结果表明ARIMA模型在对股票数据进行短期预测时只能提取出序列中的线性相关关系，其预测效果不如ARIMA模型与LSTM神经网络模型搭建的混合模型。同时通过太平鸟股票对所建立的混合模型进行验证，表明该混合模型同样能够对太平鸟股票数据进行较高精度的预测，即所建立的ARIMA-LSTM混合模型具有一定的泛化能力。

项目基金

国家级大学生创新创业训练计划项目(202111058036)，宁波市自然科学基金(2021J144)。

参考文献

[1]	吴玉霞, 温欣. 基于ARIMA模型的短期股票价格预测[J]. 统计与决策, 2016(23): 83-86.
[2]	齐天铧. 基于灰色模型与ARIMA模型的股票价格预测[J]. 计算机时代. 2021(10): 83-85+89.
[3]	黄超斌, 程希明. 基于LSTM神经网络的股票价格预测研究[J]. 北京信息科技大学学报(自然科学版), 2021, 36(1): 79-83.
[4]	夏丽. 基于ARIMA模型及回归分析的区域用电量预测方法研究[D]: [硕士学位论文]. 南京: 南京理工大学, 2013.
[5]	杨宇塬, 张梅. 基于ARIMA模型的股票价格实证分析[J]. 科技资讯, 2021, 19(29): 121-123+127.
[6]	王越敬. 基于LSTM-ARIMA混合模型的股价相关系数预测模型研究[D]: [硕士学位论文]. 绵阳: 西南科技大学, 2020.