点连接传递系数和耦合损耗因子的计算

期刊菜单

点连接传递系数和耦合损耗因子的计算
Calculation of the Point Connection Transfer Coefficient and the Coupling Loss Factor

DOI:10.12677/AAM.2022.116427,PDF,下载: 343浏览: 537
作者:钟策^*,陈赫,刘引,朱浩：上海索辰信息科技股份有限公司，上海
关键词:点连接；耦合损耗因子；传递系数；Point Junction；Coupling Loss Factor (CLF)；Transfer Coefficient

摘要:该分析涉及到计算在某一点上耦合的任意数量的结构分量之间的弹性波传输系数和耦合损耗因子。给出了解决该问题的一般方法，并证明了所产生的耦合损失因子满足互易性。该方法的一个关键方面是考虑二维分量中的圆柱波，这是建立在最近关于用圆柱坐标表示的漫射波场的能量学的结果之上的。结合入射波类型及入射波幅度计算出各板的响应位移，然后得到对应的响应波幅度，根据波幅度及类型可计算出波功率，进而计算出传递系数。根据净功率流表达式，结合模态密度变化得到子系统之间传递的耦合损耗因子，同时讨论了入射波是板入射和梁入射的情况。给出了梁和薄板构件的具体方法，并给出了一些实例。

Abstract:This analysis is concerned with the calculation of the elastic wave transmission coefficients and cou-pling loss factors among an arbitrary number of structural components that are coupled at a point. A general approach to the problem is presented and it is demonstrated that the resulting coupling loss factors satisfy reciprocity. A key aspect of the method is the consideration of cylindrical waves in two-dimensional components, and this builds upon recent results regarding the energetics of diffuse wavefields when expressed in cylindrical coordinates. The response displacement of each plate is calculated combined with the incident wave type and the incident wave amplitude, and then the corresponding response wave amplitude is obtained. The wave power can be calculated according to the wave amplitude and type, and then the transmission coefficient can be calculated. We discuss the coupling loss factor of the transmission between subsystems where the incident wave is plate incident and beam incident. Specific details of the method are given for beam and thin plate components, and a number of examples are presented.

文章引用：钟策, 陈赫, 刘引, 朱浩. 点连接传递系数和耦合损耗因子的计算[J]. 应用数学进展, 2022, 11(6): 3986-4002. https://doi.org/10.12677/AAM.2022.116427

1. 引言

耦合结构构件间弹性波传递系数的计算是结构声学研究的一个热点问题。例如，在统计能量分析模型中，常用波传递系数来确定子系统之间的耦合损耗因子。耦合损耗因子对预测复杂结构中的振动能量分布起着关键作用。

1990年Langley和Heron给出了沿无限大梁耦合的任意数半无限大板结构之间的波透射系数的一般推导。分析是基于傅立叶级数将板的响应分解为各种入射波和反射波分量。1994年Langley将分析扩展到弯曲壳体。在许多情况下，各种子结构之间的连接不是连续的，而是以许多离散点连接的形式存在。在低频率下，当波长比连接点之间的间距长时，这种连接表现为连续的线连接。然而，当波长与连接间距相当时，这种方法就不再有效了。在高频和随机间隔点连接，各连接点的运动变得不连贯，各点的连接可以单独分析。

原则上，由Heron、Bosmans和Nightingale的方法可以用来确定单个点连接的响应。然而，这种方法需要考虑大量的迹波数，以实现发生在连接点上的散射的准确描述。考虑到与这种计算相关的计算费用，人们考虑是否存在计算效率更高的替代方法。

本文给出了任意数目的半无限梁与无限板在一点连接处耦合的弹性波传递系数和耦合损耗因子的一般推导。梁和板可以以任何给定的角度定向，内部动力学和结点的有限尺寸可以通过使用动态刚度矩阵来充分考虑。分析假设，子结构通过一些无质量的刚性盘连接到连接处。结果表明，SEA互易性适用于这种连接。

本文提出了一种计算在某一点上耦合的各分量之间的波传递系数和耦合损耗因子的通用方法。计算结果表明，在所有情况下，本文方法得到的耦合损耗因子均满足互易性。

2. 点连接耦合损耗因子

2.1. 点连接介绍

设点连接表示任意数量的结构(板、梁)通过一点耦合在一起，如下图1所示，其中任一个分量j都有一个内嵌的刚性无质量圆盘与耦合点进行连接。圆盘j在直角坐标系下有六个自由度，包括平动自由度 $(w_{j 1}, w_{j 2}, w_{j 3})$ ，以及转动自由度 $(w_{j 4}, w_{j 5}, w_{j 6})$ 。基于波理论，点连接用来计算在给定角频率 $ω$ 下从任一组件入射的单位幅度的弹性波(可表示为 $\exp (i ω t)$ )，在经过点连接之后于所有组件产生的响应波幅度。点连接处的位移连续性及力平衡性将用来组建平衡方程 [1]。

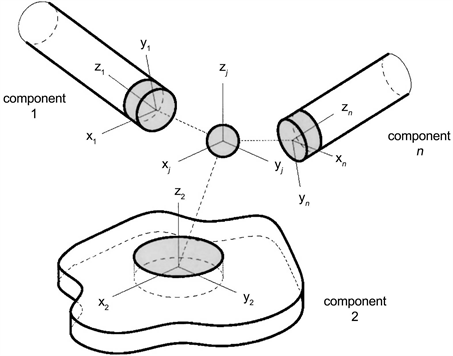
Figure 1. A general point connection among an arbitrary number of structural components

图1. 任意数量结构组成的点连接

2.2. 位移连续性条件

所有的组件都基于半无限假设，即考虑第j个组件时，若该组件没有入射波，则只存在从连接点处出发的波(包括行波和消散波)，不存在经其余边界反射的波。在这种情况下，薄梁组件包含六种波，其中四种为行波：Torsion波，Extension波，两个平面的Bending波 [2]；剩余两种为消散波：对应两个平面的Bending波。薄板组件包含十一种波，其中八种为行波：三种Bending波，两种Longitudinal波，三种Shear波；剩余三种为消散波：对应三种Bending波。对于组件j，其与连接点相连的圆盘处由响应波产生的位移向量为 $ω_{j}$ ，由组件内不同响应波产生的位移叠加而成。

$ω_{j} = \sum_{k} q_{1 j k} α_{j k} = Q_{1 j} α_{j}$ (1)

其中 $α_{j k}$ 表示组件j的第k种响应波幅度， $q_{1 j k}$ 表示其对应的位移向量， $α_{j}$ 表示响应波幅度向量，矩阵 $Q_{1 j}$ 的第k列即为向量 $q_{1 j k}$ 。位移向量 $ω_{j}$ 的维度为(6 × 1)，矩阵 $Q_{1 j}$ 不一定为方阵，对于梁 $Q_{1 j}$ 的维度为(6 × 6)，对于板 $Q_{1 j}$ 的维度为(6 × 11)。

对于板组件，圆盘四周与板需保持位移连续性，由此可推出板圆盘位移附加关系：

$Q_{2 j} α_{j} = 0$ (2)

其中， $Q_{1 j}$ 的维度为(5 × 11)。将公式(1)与公式(2)组合可得：

$Q_{j} α_{j} = (\begin{matrix} Q_{1 j} \\ Q_{2 j} \end{matrix}) α_{j} = (\begin{matrix} ω_{j} \\ 0 \end{matrix})$ (3)

对于板组件，将方阵 $Q_{j}$ 求逆可得：

$α_{j} = Q_{j}^{- 1} (\begin{matrix} ω_{j} \\ 0 \end{matrix}) = (\begin{matrix} P_{j} & R_{j} \end{matrix}) (\begin{matrix} ω_{j} \\ 0 \end{matrix})$ (4)

其中， $P_{j}$ 的维度为(11 × 6)， $R_{j}$ 的维度为(11 × 5)。

对于梁组件，则：

$α_{j} = P_{j} ω_{j}$ (5)

公式(4)与公式(5)表示组件位移与响应波幅度的关系。

2.3. 组件弹性力

内嵌圆盘施加在第j个组件的弹性力可表示为：

$F_{j} = S_{j} α_{j}$ (6)

其中矩阵 $S_{j}$ 详见第二章与第三章。对于板组件矩阵 $S_{j}$ 的维度为(6 × 11)，对于梁组件矩阵 $S_{j}$ 的维度为(6 × 6)。

将公式(5)带入公式(6)可得：

$F_{j} = S_{j} P_{j} ω_{j} = D_{j} ω_{j}$ (7)

其中，矩阵 $D_{j}$ 为动刚度矩阵，其维度为(6 × 6)。在振动噪声领域，更习惯适用阻抗矩阵，可表示为 $Z_{j} = D_{j} / i ω$ ，在此即为组件的点阻抗矩阵，将其求导可得导纳矩阵。

2.4. 入射波影响

公式(1)~(7)是基于组件j只存在响应波进行的推导，若同时存在入射波，则需要对公式进行修改。位移关系公式(3)变为：

$Q_{j} α_{j} + (\begin{matrix} ω_{i n} \\ q_{i n} \end{matrix}) α_{j} = (\begin{matrix} ω_{j} \\ 0 \end{matrix})$ (8)

其中 $α_{i n}$ 表示入射波幅度值， $ω_{i n}$ 为单位幅度入射波在圆盘产生的位移向量， $q_{i n}$ 为公式(2)所示板组件的位移约束关系所产生，若组件为梁则无此项。同理，弹性力关系式(6)修改为：

$F_{j} = S_{j} α_{j} + F_{i n} α_{i n}$ (9)

其中， $F_{i n}$ 为单位幅度入射波在圆盘产生的弹性力。根据公式(8)可知，在存在入射波情况下：

$α_{j} = Q_{j}^{- 1} (\begin{matrix} ω_{j} \\ 0 \end{matrix}) - Q_{j}^{- 1} (\begin{matrix} ω_{i n} \\ q_{i n} \end{matrix}) α_{i n}$ (10)

将公式(10)带入公式(9)并依据公式(4)对矩阵 $Q_{j}^{- 1}$ 进行替换可得：

$F_{j} = D_{j} ω_{j} + [F_{i n} - S_{j} (P_{j} ω_{i n} + R_{j} q_{i n})] α_{i n}$ (11)

在上式右端项中，除了响应波位移 $ω_{j}$ 为待解项，其余项均为已知量。若组件为梁，则公式(11)中的 $R_{j}$ 与 $q_{i n}$ 应消去。

2.5. 组装平衡方程

若连接点处受力只有入射波及各组件响应波所产生的力，则依据受力平衡，所有组件的弹性力 $F_{j}$ 求和应为0。根据公式(7)及公式(11)可得：

$\sum_{j = 1}^{N c} D_{j} ω_{j} = - [F_{i n} - S_{r} (P_{r} ω_{i n} + R_{r} q_{i n})] α_{i n}$ (12)

其中Nc表示组件数量，r表示入射波所在组件编号。由于点连接处位移连续性，各组件位移相等，因此可得组件圆盘平动位移在组件局部坐标系与全局坐标系的转换关系：

$(\begin{matrix} x \\ y \\ z \end{matrix}) = (x_{0}, y_{0}, z_{0}) ω_{j} = R_{j} (\begin{matrix} x_{j} \\ y_{j} \\ z_{j} \end{matrix})$ (13)

其中列向量 $x_{0}$ 表示局部坐标系 $x_{j}$ 轴在全局坐标系的单位投影向量，同理可得 $y_{0}$ 及 $z_{0}$ 。对于转动自由度矩阵转换关系同平动自由度一致。因此可得：

$ω_{j} = T_{j} ω$ (14)

其中，转换矩阵 $T_{j}$ 为：

$T_{j} = (\begin{matrix} R_{j}^{T} & 0 \\ 0 & R_{j}^{T} \end{matrix})$ (15)

上式中矩阵R维度为(3 × 3)，矩阵 $T_{j}$ 维度为(6 × 6)。

2.6. 波传递系数计算

在选定组件作为入射组件，给定入射波类型及入射波幅度 $α_{i n}$ 情况下，可根据公式(12)计算出各板响应位移 $ω_{j}$ ，若组件不是入射组件，则根据公式(4)或公式(5)计算出对应的响应波幅度 $α_{j}$ ，若组件为入射组件则根据公式(8)计算出对应的响应波幅度 $α_{j}$ 。根据波幅度及类型可计算出波功率，进而计算出传递系数。波功率计算公式如下：

$P = e c_{g}$ (16)

其中e为能量密度， $c_{g}$ 为群速度。

对于梁组件能量密度有：

$e = m ω^{2} | A^{2} | / 2$ (17)

其中A为波幅度。能量密度为动能能量密度与势能能量密度之和，对于远场波为动能密度的2倍，又因为波做简谐运动，1/2系数表示有效值。当梁组件波为Bending波、Extension波时，m为梁单位长度质量，若波为Torsional波，m为梁单位长度转动惯量。

对于板组件能量密度有：

$e = α | A^{2} |$ (18)

由于点连接在板组件产生的波为柱面波，波形可分为径向对称与非对称两种，若为径向对称波，则 $α = 2 m ω c$ ，若为非对称波 $α = m ω c$ 。其中m为板组件单位面积质量，c为波的相速度。

对于板的八种行波，只有两种为对称波，分别是由垂向位移及垂向转动激起的波形，对应于 $a_{0}^{(b)}$ 及 $a_{0}^{(s)}$ 两种波。

由波功率做比可得波的传递系数：

$τ_{j k} = P_{k} / P_{j}$ (19)

其中j表示入射波，k表示响应波。

2.7. 耦合损耗因子

在SEA中两个耦合子系统之间的净功率流表达式为：

$P_{j k} = ω η_{j k} η_{j} (E_{j} / n_{j} - E_{k} / n_{k})$ (20)

上式右侧为从子系统j到子系统k的功率减去从子系统j到子系统k的功率，其中E表示子系统中对应波的振动能量(时间平均动能的两倍)，n表示对应波的模态密度， $η_{j k}$ 表示子系统j到子系统k的耦合损耗因子。上述“子系统”并非狭义子系统，可扩展为不同类型的波。

梁子系统与板子系统所载波的模态密度表达式如下：

$n_{1 - D} = L / (π c_{g})$ (21)

$n_{2 - D} = ω A / (2 π c_{g})$ (22)

其中，L为梁的长度，A为板的面积。

1) 板入射情况

根据统计能量法的假设，每个子系统所载波长为扩散波长，即每个方向的行波具有相同的波强度。入射波j的平均功率可表示为：

$P = E_{j} c_{j} c_{g j} / (ω A)$ (23)

由入射波j所激起的响应波功率可表达为：

$P_{j k} = τ_{j k} E_{j} c_{j} c_{g j} / (ω A)$ (24)

令公式(24)右侧与公式(20)右侧第一项相等，并结合公式(22)可得：

$η_{j k} η_{j} = \frac{1}{2 π ω} τ_{j k}$ (25)

$η_{j k} = \frac{c_{g j} c_{j}}{ω^{2} A} τ_{j k}$ (26)

2) 梁入射情况

梁入射情况下入射波平均功率可表示为：

$P = c_{g k} E_{k} / (2 L)$ (27)

其中 $E_{k}$ 为梁子系统k类型波的振动能量， $E_{k} \ L$ 表示对应的能量密度，因为梁子系统的扩散波假设，射入连接点的波平均能量为平均能量的一半。由入射波k激起的响应波j的功率可表示为：

$P_{k j} = τ_{k j} E_{k} c_{g k} / (2 L)$ (28)

与板子系统同理可得：

$η_{k j} η_{k} = \frac{1}{2 π ω} τ_{k j}$ (29)

$η_{k j} = \frac{c_{g k}}{2 ω L} τ_{k j}$ (30)

3. 梁弹性波性质

本章将给出公式(11)中与梁子系统相关的矩阵表达式。如图2所示，考虑欧拉–伯努利梁进行分析。

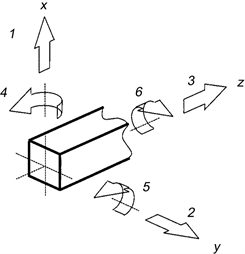
Figure 2. Coordinate system and degrees of freedom numbering at the end of a beam component

图2. 梁组件末端的坐标系和自由度编号度

下述分析基于梁形心与剪心重合，并且连接点处位于梁局部坐标 $z = 0$ 处。

考虑从连接点出发的响应波，公式(1)所示响应波幅度 $α_{j}$ 与子系统位移 $ω_{j}$ 转换矩阵 $Q_{1 j}$ 由下式可知：

$ω_{j} = Q_{1 j} α_{j} = (\begin{matrix} 1 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & i k_{b y} & 0 & 0 & 0 & k_{b y} \\ - i k_{b x} & 0 & 0 & 0 & - k_{b x} & 0 \\ 0 & 0 & 0 & 1 & 1 & 0 \end{matrix}) (\begin{matrix} α_{b x} \\ α_{b y} \\ α_{e} \\ α_{t} \\ α_{b x n} \\ α_{b y n} \end{matrix})$ (31)

不同类型波的波数为：

$k_{t}^{2} = ω^{2} \frac{ρ J}{G Q}, k_{e}^{2} = ω^{2} \frac{ρ}{E}, k_{b x}^{4} = ω^{2} \frac{m}{B_{x}}, k_{b y}^{4} = ω^{2} \frac{m}{B_{y}}$ (32)

其中G为剪切模量，E为杨氏模量， $ρ$ 为密度，m为梁单位长度质量，J为梁截面极矩(polar momen of area)，Q为扭转常数，GQ为扭转刚度， $B_{x}$ 与 $B_{y}$ 分别为y轴与x轴的弯曲刚度。 $α_{b x}$ 与 $α_{b y}$ 分别表示可引起梁x向与y向位移的行波弯曲波幅度， $α_{b x n}$ 与 $α_{b y n}$ 分别为对应的消散弯曲波，消散波不传递能量。 $α_{e}$ 与 $α_{t}$ 分别表示拉伸波与扭转波幅度。对于梁子系统， $Q_{1 j}$ 矩阵为方阵，不需要公式(3)中的 $Q_{2 j}$ 进行约束，同时公式(4)中梁对应的 $R_{j}$ 矩阵为0。将 $Q_{1 j}$ 求逆即可得公式(12)中所示 $p_{j}$ 矩阵：

$α_{j} = P_{j} ω_{j} = (\begin{matrix} (1 + i) / 2 & 0 & 0 & 0 & (1 + i) / 2 k_{b x} & 0 \\ 0 & (1 + i) / 2 & 0 & - (1 + i) / 2 k_{b y} & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ (1 - i) / 2 & 0 & 0 & 0 & - (1 + i) / 2 k_{b x} & 0 \\ 0 & (1 - i) / 2 & 0 & (1 + i) / 2 k_{b y} & 0 & 0 \end{matrix}) (\begin{matrix} u \\ v \\ w \\ θ_{x} \\ θ_{y} \\ θ_{z} \end{matrix})$ (33)

沿正Z向传递的弯曲行波弯矩M和剪力F以位移u可表示为:

$M = - B \frac{\partial^{2} u}{\partial z^{2}}, F = - B \frac{\partial^{3} u}{\partial z^{3}}$ (34)

弯矩和剪力如图3所示：

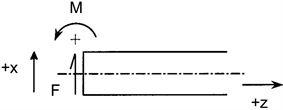
Figure 3. Positive sign convention for shear force and bending moment in a beam

图3. 梁的弯矩和剪切力示意图

公式(6)可表示为：

$(\begin{matrix} f_{u} \\ f_{v} \\ f_{w} \\ M_{θ x} \\ M_{θ y} \\ M_{θ z} \end{matrix}) = S_{j} α_{j} = (\begin{matrix} i B_{x} k_{b x}^{3} & 0 & 0 & 0 & - B_{x} k_{b x}^{3} & 0 \\ 0 & i B_{y} k_{b y}^{3} & 0 & 0 & 0 & - B_{y} k_{b y}^{3} \\ 0 & 0 & i k_{e} E A & 0 & 0 & 0 \\ 0 & - B_{y} k_{b y}^{2} & 0 & 0 & 0 & B_{y} k_{b y}^{2} \\ B_{x} k_{b x}^{2} & 0 & 0 & 0 & - B_{x} k_{b x}^{2} & 0 \\ 0 & 0 & 0 & i k_{t} G Q & O & 0 \end{matrix}) (\begin{matrix} α_{b x} \\ α_{b y} \\ α_{e} \\ α_{t} \\ α_{b x n} \\ α_{b y n} \end{matrix})$ (35)

因此可根据公式(7)推出动刚度矩阵D：

$D = (\begin{matrix} (i - 1) B_{x} k_{b x}^{3} & 0 & 0 & 0 & i B_{x} k_{b x}^{2} & 0 \\ 0 & (i - 1) B_{y} k_{b y}^{3} & 0 & - i B_{y} k_{b y}^{2} & 0 & 0 \\ 0 & 0 & i k_{e} E A & 0 & 0 & 0 \\ 0 & - i B_{y} k_{b y}^{2} & 0 & (1 + i) B_{y} k_{b y} & 0 & 0 \\ i B_{x} k_{b x}^{2} & 0 & 0 & 0 & (1 + i) B_{x} k_{b x} & 0 \\ 0 & 0 & 0 & 0 & O & i G Q k_{t} \end{matrix})$ (36)

上式与文献 [2] 中的梁阻抗矩阵保持一致。

对于任一单位幅度梁入射波，公式(8)中的 $ω_{i n}$ 可通过将公式(31)中 $Q_{1 j}$ 矩阵的对应列的波数k替换为−k得到。同理，公式(11)中的 $F_{i n}$ 可通过将公式(35)中 $S_{j}$ 矩阵的对应列的波数k替换为−k得到。

4. 板弹性波性质

4.1. 位移

通过点连接耦合的板子系统，可等效为通过一个内嵌在板中的刚性无质量圆盘与连接点相连，如图4所示。

图4所示圆盘位移共有六自由度，采用直角坐标系表示，板位移采用极坐标系表示，有三个自由度(垂向、径向、周向)。

内嵌圆盘在板上激发的波为柱面波，柱面波是指波阵面为一系列同心圆的波形。板子系统中的弯曲波可分为三种：分别由圆盘平面外位移 $ω$ 及旋转 $θ_{x}$ 和 $θ_{y}$ 激发产生，对应行波幅度表示为 $α_{0}^{(b)}$ 、 $α_{1 s}^{(b)}$ 、 $α_{1 c}^{(b)}$ ，每种弯曲行波分别对应一种弯曲消散波，幅度表示为 $α_{0}^{(b n)}$ 、 $α_{1 s}^{(b n)}$ 、 $α_{1 c}^{(b n)}$ 。板子系统中的纵波可分为两种：分别由圆盘平面内位移u和v激发产生，对应波形幅度表示为 $α_{1 c}^{(e)}$ 、 $α_{1 s}^{(e)}$ 。板子系统中的剪切波可分为三种：前两种分别由圆盘平面内位移u和v激发产生，第三种由旋转 $θ_{z}$ 激发产生，三种波对应波形幅度表示为 $α_{1 s}^{(s)}$ 、 $α_{1 c}^{(s)}$ 、 $α_{0}^{(s)}$ 。综上，圆盘位移及波形对应关系如表1所示。

由于板子系统通过圆盘激发的波为柱面波，板子系统按照图4所示极坐标进行表示。

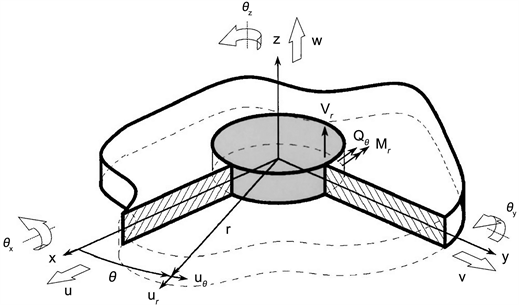
Figure 4. Coordinate systems used to describe displacement of a disc embedded in a thin plate and the associated forces and moments

图4. 板子系统及内嵌圆盘的力和力矩示意图

Table 1. Disk-displacement excitation plate subsystem waveform

表1. 圆盘位移激发板子系统波形

板子系统在极坐标下的平面外位移可由六种弯曲波平面外位移求和得到：

$\begin{matrix} u_{z} (r, θ) = α_{0}^{(b)} H_{0}^{(2)} (k_{b} r) + α_{1 c}^{(b)} H_{1}^{(2)} (k_{b} r) \cos θ + α_{1 s}^{(b)} H_{1}^{(2)} (k_{b} r) \sin θ \\ + α_{0}^{(b n)} H_{0}^{(2)} (- i k_{b} r) + α_{1 c}^{(b n)} H_{1}^{(2)} (- i k_{b} r) \cos θ + α_{1 s}^{(b n)} H_{1}^{(2)} (- i k_{b} r) \sin θ \end{matrix}$ (37)

其中， $H_{n}^{(2)}$ 表示阶数为n的第二类汉克尔函数，r和 $θ$ 表示内嵌圆盘与板子系统临界中面位置在极坐标下的坐标值。r值的选取见本节备注。 $k_{b}$ 表示在给定角频率 $ω$ 下的弯曲波数：

$k_{b} = {(m / D)}^{1 / 4} ω^{1 / 2}$ (38)

其中m是板的单位面积质量，D是板的弯曲刚度。板子系统在极坐标下的平面内位移由纵波与剪切波耦合导致，位移表达式可由纵波势 $ψ$ 及剪切波势 $ϕ$ 得到：

$u_{r} (r, θ) = \frac{\partial ψ}{\partial r} + \frac{1}{r} \frac{\partial ϕ}{\partial θ}$ (39)

$u_{θ} (r, θ) = \frac{1}{r} \frac{\partial ψ}{\partial θ} - \frac{\partial ϕ}{\partial r}$ (40)

其中， $u_{r}$ 和 $u_{θ}$ 分别是板在极坐标下的径向位移和周向位移。根据文献 [3] 纵波势 $ψ$ 及剪切波势 $ϕ$ 表达式为：

$\begin{array}{l} k_{e} ψ (r, θ) = α_{1 c}^{(e)} H_{1}^{(2)} (k_{e} r) \cos θ + α_{1 s}^{(e)} H_{1}^{(2)} (k_{e} r) \sin θ \\ k_{s} ϕ (r, θ) = α_{0}^{(s)} H_{0}^{(2)} (k_{s} r) \cos θ + α_{1 c}^{(s)} H_{1}^{(2)} (k_{s} r) \cos θ + α_{1 s}^{(s)} H_{1}^{(2)} (k_{s} r) \sin θ \end{array}$ (41)

纵波波数 $k_{e}$ 与剪切波波数 $k_{s}$ 表达式如下：

$k_{e} = ω \sqrt{ρ (1 - v^{2}) / E}, k_{s} = ω \sqrt{ρ / G}$ (42)

其中， $ρ$ 为板材料密度，v为泊松比，E为杨氏模量，G为剪切模量。

公式(37)与公式(39)、公式(40)给出了在圆盘激励的11种柱面波所导致的板位移表达式。为了进一步推导出公式(12)中的板矩阵，需要结合位圆盘与盘边界处位移连续性条件及力平衡条件。

4.2. 连续性条件

1) 平面外位移

在板极坐标 $(r = a, θ, z = 0)$ ，即圆盘与板交界处需满足垂向位移连续性条件，此处板垂向位移为 $u_{z}$ 。圆盘的三个自由度 $ω$ 、 $θ_{x}$ 、 $θ_{y}$ 都会导致垂向位移产生，分别为 $ω$ 、 $(a \sin θ) θ_{x}$ 、 $- (a \cos θ) θ_{y}$ ，其中 $a \sin θ$ 与 $a \cos θ$ 分别为在角度 $θ$ 处绕X轴、Y轴的旋转半径。根据板垂向位移与圆盘垂向位移连续可得：

$u_{z} (a, θ) = ω + a θ_{x} \sin θ - a θ_{y} \cos θ$ (43)

将公式(37)代入上式，根据等式两边 $\sin θ$ 项、 $\cos θ$ 项、与 $θ$ 无关项对应相等可得三个独立的方程。三组独立方程可得到公式(1)中的弯曲波与圆盘位移对应方程组：

$ω = α_{0}^{(b)} H_{0}^{(2)} (k_{b} r) + α_{0}^{(b n)} H_{0}^{(2)} (- i k_{b} r)$ (44)

$a θ_{x} \sin θ = α_{1 s}^{(b)} H_{1}^{(2)} (k_{b} r) \sin θ + α_{1 s}^{(b n)} H_{1}^{(2)} (- i k_{b} r) \sin θ$ (45)

$- a θ_{y} \cos θ = α_{1 c}^{(b)} H_{1}^{(2)} (k_{b} r) \cos θ + α_{1 c}^{(b n)} H_{1}^{(2)} (- i k_{b} r) \cos θ$ (46)

同时圆盘与板可以看作严格夹紧地，即垂向位移在径向需满足一阶连续，将公式(43)两边分别对径向坐标r求导可得：

$\frac{\partial u_{z} (a, θ)}{\partial r} - θ_{x} \sin θ + θ_{y} \cos θ = 0$ (47)

将公式(37)代入上式，根据等式两边 $\sin θ$ 项、 $\cos θ$ 项、与 $θ$ 无关项对应相等可得三个独立的方程，这三组方程为弯曲波附加项，对应公式(2)中的弯曲波附加条件项：

$k_{b} α_{0}^{(b)} H_{0}^{(2)'} (k_{b} r) + (- i k_{b}) α_{0}^{(b n)} H_{0}^{(2)'} (- i k_{b} r) = 0$ (48)

$[k_{b} H_{1}^{(2)'} (k_{b} r) - \frac{1}{a} H_{1}^{(2)} (k_{b} r)] α_{1 c}^{(b)} + [- i k_{b} H_{1}^{(2)'} (- i k_{b} r) - \frac{1}{a} H_{1}^{(2)} (- i k_{b} r)] α_{1 c}^{(b n)} = 0$ (49)

$[k_{b} H_{1}^{(2)'} (k_{b} r) - \frac{1}{a} H_{1}^{(2)} (k_{b} r)] α_{1 s}^{(b)} + [- i k_{b} H_{1}^{(2)'} (- i k_{b} r) - \frac{1}{a} H_{1}^{(2)} (- i k_{b} r)] α_{1 c}^{(b n)} = 0$ (50)

2) 平面内位移

圆盘与板平面内位移也需满足连续性条件：

$u_{r} (a, θ) = u \cos θ + v \sin θ$ (51)

$u_{θ} = a θ_{z} - u \sin θ + v \cos θ$ (52)

使得公式(39)、公式(40)与公式(51)、公式(52)右边项相等，并令等式两边 $\sin θ$ 项、 $\cos θ$ 项、 $θ$ 无关项对应相等，可得：

$u \cos θ = α_{1 c}^{e} H_{1}^{{(2)}^{'}} (k_{e} r) \cos θ + \frac{α_{1 s}^{(s)}}{r k_{s}} H_{1}^{(2)} (k_{s} r) \cos θ$ (53)

$u \sin θ = α_{1 s}^{e} H_{1}^{(2)'} (k_{e} r) \sin θ - \frac{α_{1 c}^{(s)}}{r k_{s}} H_{1}^{(2)} (k_{s} r) \sin θ$ (54)

$a θ_{z} = - α_{0}^{(s)} H_{0}^{(2)'} (k_{s} r)$ (55)

$u \sin θ = \frac{α_{1 c}^{(e)}}{r k_{e}} H_{1}^{(2)} (k_{e} r) \sin θ + α_{1 s}^{s} H_{1}^{(2)'} (k_{s} r) \sin θ$ (56)

$u \cos θ = \frac{α_{1 s}^{(e)}}{r k_{e}} H_{1}^{(2)} (k_{e} r) \cos θ - α_{1 c}^{(s)} H_{1}^{(2)'} (k_{s} r) \cos θ$ (57)

公式(53)~公式(55)可以推得圆盘平面内位移与波幅度关系，同时分别结合公式(53)与公式(56)，结合公式(54)与公式(57)可得波幅度之间的约束关系：

$u = α_{1 c}^{e} H_{1}^{(2)'} (k_{e} r) + \frac{α_{1 s}^{(s)}}{r k_{s}} H_{1}^{(2)} (k_{s} r)$ (58)

$v = α_{1 s}^{e} H_{1}^{(2)'} (k_{e} r) - \frac{α_{1 c}^{(s)}}{r k_{s}} H_{1}^{(2)} (k_{s} r)$ (59)

$θ_{z} = - \frac{α_{0}^{(s)}}{a} H_{0}^{(2)'} (k_{s} r)$ (60)

$[H_{1}^{(2)'} (k_{e} r) - \frac{H_{1}^{(2)} (k_{e} r)}{r k_{e}}] α_{1 c}^{(e)} + [- H_{1}^{(2)'} (k_{s} r) + \frac{H_{1}^{(2)} (k_{s} r)}{r k_{s}}] α_{1 s}^{(s)} = 0$ (61)

$[H_{1}^{(2)'} (k_{e} r) - \frac{H_{1}^{(2)} (k_{e} r)}{r k_{e}}] α_{1 s}^{(e)} + [H_{1}^{(2)'} (k_{s} r) - \frac{H_{1}^{(2)} (k_{s} r)}{r k_{s}}] α_{1 c}^{(s)} = 0$ (62)

综合公式(44~46)、公式(58~60)可得到公式(3)中的 $Q_{1 j}$ 矩阵，综合公式(48~50)、公式(61~62)可得到公式(3)中的 $Q_{2 j}$ 矩阵。其中 $Q_{1 j}$ 矩阵如下所示：

$(\begin{matrix} u \\ v \\ w \\ θ_{x} \\ θ_{y} \\ θ_{z} \end{matrix}) = (\begin{matrix} 0 & 0 & 0 & B_{3} & 0 & 0 \\ 0 & 0 & 0 & 0 & B_{3} & 0 \\ B_{1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & B_{2} & 0 & 0 & 0 \\ 0 & - B_{2} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & O & B_{5} \end{matrix} \begin{matrix} 0 & B_{4} & 0 & 0 & 0 \\ - B_{4} & 0 & 0 & 0 & 0 \\ 0 & 0 & B_{1 n} & 0 & 0 \\ 0 & 0 & 0 & 0 & B_{2 n} \\ 0 & 0 & 0 & - B_{2 n} & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}) (\begin{matrix} α_{0}^{(b)} \\ α_{1 c}^{(b)} \\ α_{1 s}^{(b)} \\ α_{1 c}^{(e)} \\ α_{1 s}^{(e)} \\ α_{0}^{(s)} \\ α_{1 c}^{(s)} \\ α_{1 s}^{(s)} \\ α_{0}^{(b n)} \\ α_{1 c}^{(b n)} \\ α_{1 s}^{(b n)} \end{matrix})$ (63)

其中各项系数如下所示：

$\begin{array}{l} B_{1} = H_{0}^{(2)} (k_{b} a), B_{1 n} = H_{0}^{(2)} (- i k_{b} a), B_{2} = \frac{1}{a} H_{1}^{(2)} (k_{b} a), B_{2 n} = \frac{1}{a} H_{1}^{(2)} (- i k_{b} a) \\ B_{3} = H_{1}^{(2)'} (k_{e} a), B_{4} = \frac{1}{k_{s} a} H_{1}^{(2)} (k_{s} a), B_{5} = - \frac{1}{a} H_{0}^{(2)'} (k_{s} a) \end{array}$ (64)

$Q_{2 j}$ 矩阵如下所示：

$Q_{2 j} = (\begin{matrix} B_{6} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & B_{6 n} & 0 & 0 \\ 0 & 0 & B_{7} - B_{2} & 0 & B_{3} & 0 & 0 & 0 & 0 & 0 & B_{7 n} - B_{2 n} \\ 0 & B_{7} - B_{2} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & B_{7 n} - B_{2 n} & 0 \\ 0 & 0 & 0 & B_{8} + B_{3} & 0 & 0 & 0 & B_{9} + B_{4} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & - B_{8} - B_{3} & 0 & B_{9} + B_{4} & 0 & 0 & 0 \end{matrix})$ (65)

其中各项系数如下所示：

$\begin{array}{l} B_{6} = k_{b} H_{0}^{(2)'} (k_{b} a), B_{6 n} = - i k_{b} H_{0}^{(2)'} (- i k_{b} a), \\ B_{7} = k_{b} H_{1}^{(2)'} (k_{b} a), B_{7 n} = - i k_{b} H_{1}^{(2)'} (- i k_{b} a), \\ B_{8} = - \frac{1}{k_{e} a} H_{1}^{(2)} (k_{e} a), B_{9} = - H_{1}^{(2)'} (k_{s} a) \end{array}$ (66)

根据公式(4)可得：

$\begin{array}{l} Q_{1 j} P_{j} = I, Q_{1 j} R_{j} = 0 \\ Q_{2 j} P_{j} = 0, Q_{2 j} R_{j} = I \end{array}$ (67)

其中I为单位矩阵。可得：

$P_{j} = (\begin{matrix} 0 & 0 & A_{1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & A_{2} & 0 \\ 0 & 0 & 0 & - A_{2} & 0 & 0 \\ A_{3} & 0 & 0 & 0 & 0 & 0 \\ 0 & A_{3} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & A_{5} \\ 0 & A_{4} & 0 & 0 & 0 & 0 \\ - A_{4} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & A_{1 n} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & A_{2 n} & 0 \\ 0 & 0 & 0 & - A_{2 n} & 0 & 0 \end{matrix})$ (68)

其中各项系数为：

$\begin{array}{l} A_{1} = \frac{H_{0}^{(2)'} (- i k_{b} a)}{H_{0}^{(2)} (k_{b} a) H_{0}^{(2)'} (- i k_{b} a) - i H_{0}^{(2)} (- i k_{b} a) H_{0}^{(2)'} (k_{b} a)}, \\ A_{2} = \frac{- H_{1}^{(2)} (- i k_{b} a) - i k_{b} a H_{1}^{(2)'} (- i k_{b} a)}{i k_{b} H_{1}^{(2)} (k_{b} a) H_{1}^{(2)'} (- i k_{b} a) + k_{b} H_{1}^{(2)} (- i k_{b} a) H_{1}^{(2)'} (k_{b} a)}, \\ A_{3} = \frac{k_{s} k_{e} a^{2} H_{1}^{(2)'} (k_{s} a) - k_{e} a H_{1}^{(2)} (k_{s} a)}{k_{s} k_{e} a^{2} H_{1}^{(2)'} (k_{s} a) H_{1}^{(2)'} (k_{e} a) - H_{1}^{(2)} (k_{s} a) H_{1}^{(2)} (k_{e} a)}, \\ A_{4} = \frac{- k_{s} k_{e} a^{2} H_{1}^{(2)'} (k_{e} a) + k_{s} a H_{1}^{(2)} (k_{e} a)}{k_{s} k_{e} a^{2} H_{1}^{(2)'} (k_{s} a) H_{1}^{(2)^{'}} (k_{e} a) - H_{1}^{(2)} (k_{s} a) H_{1}^{(2)} (k_{e} a)}, \end{array}$

$\begin{array}{l} A_{5} = - \frac{a}{H_{0}^{(2)'} (k_{s} a)}, \\ A_{1 n} = \frac{- i H_{0}^{(2)'} (k_{b} a)}{H_{0}^{(2)} (k_{b} a) H_{0}^{(2)'} (- i k_{b} a) - i H_{0}^{(2)} (- i k_{b} a) H_{0}^{(2)'} (k_{b} a)}, \\ A_{2 n} = \frac{i H_{1}^{(2)} (k_{b} a) - i k_{b} a H_{1}^{(2)'} (k_{b} a)}{i k_{b} H_{1}^{(2)} (- i k_{b} a) H_{1}^{(2)'} (k_{b} a) - k_{b} H_{1}^{(2)} (k_{b} a) H_{1}^{(2)'} (- i k_{b} a)} \end{array}$ (69)

上述推导的 $P_{j}$ 矩阵为板j响应波的表达式，将与下节推导的 $S_{j}$ 一起推导出动刚度矩阵 $D_{j}$ 。

对于单位幅度入射波， $ω_{i n}$ 向量为 $Q_{1 j}$ 矩阵中的对应列向量， $q_{i n}$ 向量为 $Q_{2 j}$ 矩阵中的对应列向量，同时因为波为入射波，需将其中的第二类汉克尔函数 $H_{n}^{(2)}$ 转为第一类汉克尔函数 $H_{n}^{(1)}$ 。据此可推出由选定板r的入射波 $P_{r} ω_{i n} + R_{r} q_{i n}$ 列向量组成的矩阵：

$(\begin{matrix} α_{0}^{(b)} & α_{1 c}^{(b)} & α_{1 s}^{(b)} & α_{1 c}^{(e)} & α_{1 s}^{(e)} & α_{0}^{(s)} & α_{1 c}^{(s)} & α_{1 s}^{(s)} \\ C_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & C_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & C_{2} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & C_{3} & 0 & 0 & 0 & - C_{6} \\ 0 & 0 & 0 & 0 & C_{3} & 0 & C_{6} & 0 \\ 0 & 0 & 0 & 0 & 0 & C_{5} & 0 & 0 \\ 0 & 0 & 0 & 0 & - C_{4} & 0 & C_{7} & 0 \\ 0 & 0 & 0 & C_{4} & 0 & 0 & 0 & C_{7} \\ C_{1 n} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & C_{2 n} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & C_{2 n} & 0 & 0 & 0 & 0 & 0 \end{matrix})$ (70)

上式矩阵第一行为板入射波，板共有十一种波，其中八种为行波，三种为消散波，入射波只有行波。上式中每种入射波对应列向量即为其对应的 $P_{r} ω_{i n} + R_{r} q_{i n}$ 向量。上式中各项系数表达式如下所示：

$\begin{array}{l} C_{1} = \frac{H_{0}^{(2)'} (- i k_{b} a) H_{0}^{(1)} (k_{b} a) - i H_{0}^{(1)'} (k_{b} a) H_{0}^{(2)} (- i k_{b} a)}{H_{0}^{(2)'} (- i k_{b} a) H_{0}^{(2)} (k_{b} a) - i H_{0}^{(2)'} (k_{b} a) H_{0}^{(2)} (- i k_{b} a)}, \\ C_{1 n} = \frac{H_{0}^{(2)'} (k_{b} a) H_{0}^{(1)} (k_{b} a) - H_{0}^{(1)'} (k_{b} a) H_{0}^{(2)} (k_{b} a)}{H_{0}^{(2)'} (k_{b} a) H_{0}^{(2)} (- i k_{b} a) + i H_{0}^{(2)'} (- i k_{b} a) H_{0}^{(2)} (k_{b} a)}, \\ C_{2} = \frac{i H_{1}^{(2)'} (- i k_{b} a) H_{1}^{(1)} (k_{b} a) + H_{1}^{(1)'} (k_{b} a) H_{1}^{(2)} (- i k_{b} a)}{H_{1}^{(2)'} (k_{b} a) H_{1}^{(2)} (- i k_{b} a) + i H_{1}^{(2)'} (- i k_{b} a) H_{1}^{(2)} (k_{b} a)}, \\ C_{2 n} = \frac{H_{1}^{(1)} (k_{b} a) H_{1}^{(2)'} (k_{b} a) - H_{1}^{(2)} (k_{b} a) H_{1}^{(1)'} (k_{b} a)}{i H_{1}^{(2)} (k_{b} a) H_{1}^{(2)'} (- i k_{b} a) + H_{1}^{(2)} (- i k_{b} a) H_{1}^{(2)'} (k_{b} a)}, \\ C_{3} = \frac{H_{1}^{(1)} (k_{e} a) H_{1}^{(2)} (k_{s} a) - a^{2} k_{e} k_{s} H_{1}^{(1)'} (k_{e} a) H_{1}^{(2)'} (k_{s} a)}{H_{1}^{(2)} (k_{e} a) H_{1}^{(2)} (k_{s} a) - a^{2} k_{e} k_{s} H_{1}^{(2)'} (k_{e} a) H_{1}^{(2)'} (k_{s} a)}, \end{array}$

$\begin{array}{l} C_{4} = \frac{a k_{s} H_{1}^{(2)'} (k_{e} a) H_{1}^{(1)} (k_{e} a) - a k_{s} H_{1}^{(1)'} (k_{e} a) H_{1}^{(2)} (k_{e} a)}{- H_{1}^{(2)} (k_{e} a) H_{1}^{(2)} (k_{s} a) + a^{2} k_{e} k_{s} H_{1}^{(2)'} (k_{e} a) H_{1}^{(2)'} (k_{s} a)}, \\ C_{5} = \frac{H_{1}^{(1)'} (k_{s} a)}{H_{0}^{(2)'} (k_{s} a)}, \end{array}$

$\begin{array}{l} C_{6} = \frac{k_{e} a H_{1}^{(1)'} (k_{s} a) H_{1}^{(2)} (k_{s} a) - k_{e} a H_{1}^{(2)'} (k_{s} a) H_{1}^{(1)} (k_{s} a)}{a^{2} k_{e} k_{s} H_{1}^{(2)'} (k_{e} a) H_{1}^{(2)'} (k_{s} a) - H_{1}^{(2)} (k_{e} a) H_{1}^{(2)} (k_{s} a)}, \\ C_{7} = \frac{H_{1}^{(1)} (k_{s} a) H_{1}^{(2)} (k_{e} a) - k_{e} k_{s} a^{2} H_{1}^{(1)'} (k_{s} a) H_{1}^{(2)'} (k_{e} a)}{H_{1}^{(2)} (k_{e} a) H_{1}^{(2)} (k_{s} a) - k_{e} k_{s} a^{2} H_{1}^{(2)'} (k_{e} a) H_{1}^{(2)'} (k_{s} a)} \end{array}$ (71)

上式中 $C_{4}$ 与 $C_{6}$ 相比论文中公式进行了修正。

4.3. 弹性力

1) 平面外位移相关的弹性力

内嵌圆盘作用在交界平板上的弹性力可分为由圆盘平面外位移引起及平面内位移引起两部分。平面外位移所引起的弹性力由剪力和弯矩组成。对于极坐标系下的板子系统剪力 $V_{r}$ 与弯矩 $M_{r}$ 如图4所示，根据文献 [4]，单位长度剪力 $V_{r}$ 与弯矩 $M_{r}$ 表达式如下：

$V_{r} (θ) = D {\frac{\partial^{3} u_{z}}{\partial r^{3}} + \frac{1}{a} \frac{\partial^{2} u_{z}}{\partial r^{2}} - \frac{1}{a^{2}} \frac{\partial u_{z}}{\partial r} - \frac{3 - ν}{a^{3}} \frac{\partial^{3} u_{z}}{\partial θ^{3}} + \frac{2 - ν}{a^{2}} \frac{\partial^{3} u_{z}}{\partial r \partial θ}}$ (72)

$M_{r} (θ) = D {\frac{\partial^{2} u_{z}}{\partial r^{2}} + \frac{ν}{a^{2}} \frac{\partial^{2} u_{z}}{\partial θ^{2}} + \frac{ν}{a} \frac{\partial u_{z}}{\partial r}}$ (73)

因此，连接点处圆盘平面外位移引起的合力如下所示：

$M_{x} = a \int_{0}^{θ^{'}} (a V_{r} - M_{r}) \sin θ d θ,$ (74)

$M_{y} = - a \int_{0}^{θ^{'}} (a V_{r} - M_{r}) \cos θ d θ,$ (75)

$F_{z} = a \int_{0}^{θ^{'}} V_{r} d θ$ (76)

其中 $θ^{'}$ 为积分角度，该角度为板子系统连接点位置在极坐标下环向角度值。将公式(37)代入公式(72)~公式(76)可得到公式(6)中弯曲波幅度与平面外位移引起弹性力的关系。

2) 平面内位移相关的弹性力

根据文献 [4] 中公式(A.32)~(A.34)可得在板极坐标下单位长度平面内应力与位移关系：

$σ_{r r} = \frac{E}{1 - ν^{2}} (\frac{\partial u_{r}}{\partial r} + \frac{ν}{r} u_{r} + \frac{ν}{r} \frac{\partial u_{θ}}{\partial θ}),$ (77)

$σ_{r θ} = G (\frac{1}{r} \frac{\partial u_{r}}{\partial θ} - \frac{u_{θ}}{r} + \frac{\partial u_{θ}}{\partial r})$ (78)

与平面外位移类似，圆盘所提供合力如下所示：

$F_{x} = - h a \int_{0}^{θ^{'}} (σ_{r r} \cos θ - σ_{r θ} \sin θ) d θ,$ (79)

$F_{y} = - h a \int_{0}^{θ^{'}} (σ_{r r} \sin θ + σ_{r θ} \cos θ) d θ,$ (80)

$M_{z} = - h a^{2} \int_{0}^{θ^{'}} (σ_{r θ} \sin θ) d θ$ (81)

其中h为板厚度。将公式(39)~公式(41)代入上式可得公式(6)中平面内波幅度与力的关系。

综上，可得公式(6)中 $S_{j}$ 矩阵表达为：

$(\begin{matrix} f_{x} \\ f_{y} \\ f_{z} \\ M_{x} \\ M_{y} \\ M_{z} \end{matrix}) = (\begin{matrix} 0 & 0 & 0 & X_{31} & 0 & 0 \\ 0 & 0 & 0 & 0 & X_{32} & 0 \\ X_{1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & X_{21} & 0 & 0 & 0 \\ 0 & - X_{22} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & O & X_{5} \end{matrix} \begin{matrix} 0 & X_{41} & 0 & 0 & 0 \\ - X_{42} & 0 & 0 & 0 & 0 \\ 0 & 0 & X_{1 n} & 0 & 0 \\ 0 & 0 & 0 & 0 & X_{21 n} \\ 0 & 0 & 0 & - X_{22 n} & 0 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}) (\begin{matrix} α_{0}^{(b)} \\ α_{1 c}^{(b)} \\ α_{1 s}^{(b)} \\ α_{1 c}^{(e)} \\ α_{1 s}^{(e)} \\ α_{0}^{(s)} \\ α_{1 c}^{(s)} \\ α_{1 s}^{(s)} \\ α_{0}^{(b n)} \\ α_{1 c}^{(b n)} \\ α_{1 s}^{(b n)} \end{matrix})$ (82)

4.4. 动刚度矩阵

根据上述推出的矩阵 $S_{j}$ 与矩阵 $P_{j}$ ，代入公式(7)可得板的动刚度矩阵 $D_{j}$ 。板的阻抗矩阵 $Z_{p l a t e}$ 可推出为：

$Z_{p l a t e} = \frac{1}{i ω} D_{j}$ (83)

5. 数值算例

5.1. 梁验证算例

考虑梁连接算例如图5所示。梁属性为 $\begin{array}{l} E = 7.2 \times 10^{10} N / m^{2}, G Q = 3.5 \times 10^{3} N \cdot m^{2}, ρ = 2710 kg / m^{3}, \\ G = 2.69 \times 10^{10} N / m^{2}, A = 4.0 \times 10^{- 4}, J = 2.83 \times 10^{- 6} m^{4}, \\ I_{x x} = 3.48 \times 10^{- 8} m^{4}, I_{y y} = 2.8 \times 10^{- 6} m^{4} \end{array}$ 梁局部坐标系y轴位于点连接平面。

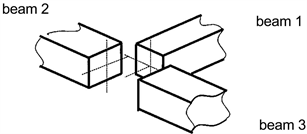
Figure 5. T-junction between three beam subsystems.

图5. 三梁子系统T型连接

如图6(a)，图6(b)所示算例结果与Moore (1990)一致。

5.2. 板梁连接算例

考虑板–梁连接算例，如图7所示。

其中板厚度3.175 mm，梁x向长度3.175 mm，y向长度38.1 mm，梁长1.3208 m，弹性模量为7.21 × 10¹⁰N/m²，密度为2170 kg/m³，泊松比为0.3。如图8所示该算例与Lyon和Eichler (1964)所用算例一致。

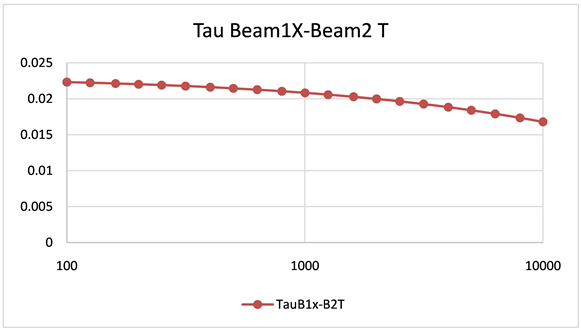(a)(b)

Figure 6. (a) Beam 1 to beam 2 point connection coupling loss factor; (b) Beam 1 to beam 2 T type connection coupling loss factor

图6. (a) 梁1至梁2点连接耦合损失因子；(b) 梁1至梁2 T型连接耦合损失因子

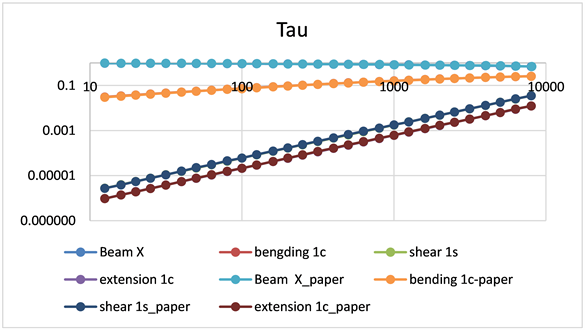
Figure 7. Beam-plate structure diagram

图7. 板梁连接图示

Figure 8. Comparison results of the coupling loss factors

图8. 耦合损失因子对比结果

6. 结论

本文提出了一种计算在某一点上耦合的各分量之间的波传递系数和耦合损耗因子的通用方法。这项工作建立在对柱状波运动的早期研究之上。计算结果表明，在所有情况下，本文方法得到的耦合损耗因子均满足互易性。包括薄板和梁组件所需的矩阵的全部细节已经给出，并给出了一些例子。

NOTES

^*通讯作者。

参考文献

[1]	Langley, R.S. and Shorter, P.J. (2003) The Wave Transmission Coefficients and Coupling Loss Factors of Point Con-nected Structures. The Journal of the Acoustical Society of America, 113, 1947-1965. https://doi.org/10.1121/1.1515791
[2]	Cremer, L., Heckl, M. and Petersson, B.A.T. (2005) Structure-Borne Sound. Springer, Berlin, 39-103.
[3]	Morfey, C.L. (1994) Cylindrical in-Plane Waves in the Elastic Plate. Journal of Sound and Vibration, 173, 557-560.
[4]	Leissa, W. (1969) Vibration of Plates. NASA, Washington DC, 11-41.

为你推荐

友情链接