1. 引言
概念性降雨径流模型是常用的洪水预报模型,新安江模型作为一种概念性降雨径流模型广泛应用于湿润地区与半湿润地区 [1],然而新安江模型含有16个参数,并且这些参数是相互依赖的,这使得参数率定十分困难,其推广与应用受到严峻挑战 [2] [3]。
目前常用的模型参数率定方法包括人工试错法与智能算法,其中人工试错法是在计算机欠发达时常用的方法,然而由于其缺少判断参数优劣判断标准,缺少客观性,并且对个人经验要求较高,当个人经验不足时很难得到理想的结果 [4]。随着计算机技术的发展,人工智能算法广泛应用于新安江模型参数率定,目前常用的方法主要有Rosenbrock [4]、SCE-UA [5] [6]、遗传算法 [7]。然而Rosenbrock与SCE-UA法在搜索过程中很容易陷入局部最优。遗传算法由于其简单通用、鲁棒性强、全局寻优等特点,常用于非解析式的目标函数与约束等问题,成为水文工作者参数率定的重要手段 [8] [9]。近些年多核计算技术的普及与发展,多核并行技术具有计算成本低廉、系统运行环境稳定、并行环境容易实现等优点,已在水资源领域广泛应用 [6] [10]。本文结合遗传算法的天然可并行性,提出来一种多核并行遗传算法,用于求解多准则新安江模型参数率定问题,以我国南方地区酉水流域凤滩水库为例,表明本文所提方法能显著提高参数率定速度。
2. 新安江及参数率定标准
模型参数的率定是一个迭代过程,不断调整参数以找到一组参数以实现模拟洪水流量与观测值之间的最佳拟合。一般来说,理想的参数模拟结果应满足两个基本条件:具有较高的合格率和对于不合格场次的洪水误差累计和较小。为此引入了模糊集的概念。
当评价目标为洪峰流量和洪水总量时,各方案对应评价目标的模糊合格率为:
(1)
式中:当
时,
为第i个方案对应洪峰流量的模糊合格率,
为第i个方案的洪峰流量实际值与预报值相对误差的绝对值;当
时,
为第i个方案对应洪水总量的模糊合格率,
为第i个方案的洪水总量实际值与预报值相对误差的绝对值;
为修正系数。
当评价目标为峰现时间时,各方案对应评价目标的模糊合格率为:
(2)
式中:当
时,
为第i个方案对应峰现时间的模糊合格率,
为第i个方案的峰现时间,所述峰现时间是指预报洪峰时间与实际洪峰时间之差。
每个方案对应不同评价目标的模糊合格率
进行归一化处理,由归一化处理后的模糊合格率
构成归一化矩阵
,其中
,
,
,
。
根据权重决策矩阵
计算正理想解
和负理想解
,具体计算为:
(3)
(4)
根据正理想解
和负理想解
,计算距正理想解的距离
和距负理想解的距离
,具体计算为:
(5)
计算评价方案与对应负理想解的相对贴近度,具体计算为:
(6)
式中:
为第i个方案与该方案对应的负理想解的相对贴近度;其中
值越大,对应的方案越优。
3. 并行计算
Fork/Join框架是Java7提供的一个充分挖掘多核CPU计算能力的并行计算框架,通过问题分解、并行计算与结果合并三个主要步骤实现并行求解。其基本思想是采用“分治策略”将计算规模较大的问题,分解为若干个规模较小、相对独立的问题进行求解,然后求得各个子问题的解,合并子问题的解得到原问题的解,其计算执行过程如图1所示。该框架通过阀值控制子问题的规模大小,任务划分时,首先判断任务规模是否大于设定的阀值,如果任务规模小于设定的阀值,则直接求解即可;如果任务规模大于设定的阀值,则对任务规模进行划分,直到子问题的任务规模小于设定的阀值。在并行过程中如果阀值过大,则子问题任务数目较小,无法充分发挥多核优势;如果阀值太小,则子问题数目较多,任务管理开销加大。为充分利用资源、提高计算效率,按下式确定阈值:
(7)
式中:
表示取最小正整数,
为阈值,p为多核CPU的核数,q为原问题的计算规模。
4. 具体流程
1) 染色体的确定:新安江模型16个参数组成的参数集相当于一个染色体,每一个参数变量相当于一个基因。本文采用十进制整数进行编码。
2) 初始化种群:假设种群规模为
,记
,其中m为种群个数,n为新安江模型参数数量,
为第i个染色体对应的第j个参数的取值。
3) 采用Fork/Join并行框架创建并行遗传算法,并将m个染色体分配到不同的线程池中。
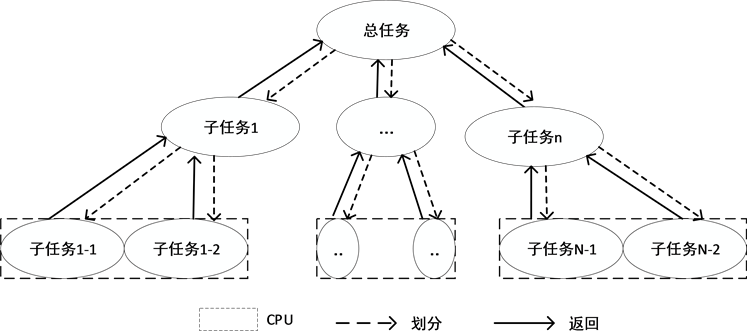
Figure 1. Flow chart of parallel computing
图1. 并行计算流程图
4) 计算各线程池中评价目标的模糊合格率。
5) 根据所述步骤4计算的模糊合格率,创建由m个方案和l个评价目标构成的多目标评价矩阵
,记
,其中
为第i个方案对应第j个评价目标的模糊合格率,
为第i个方案对应的目标向量,记为
。
6) 根据所述多目标评价矩阵
计算并确定各线程池中的最优方案,将各线程池对应的最优方案返回给主线程。
7) 所述主线程对各线程池对应的最优方案进行比对,确定当前最优计算结果。
8) 根据所述步骤7的当前最优计算结果确定该当前最优计算结果对应的方案,从而确定模型的当前参数组合。
9) 对于所述步骤8的当前参数组合,计算该当前参数组合中各参数在不同水平下相对贴近度
的平均值
,选取平均值
中的最大值
所对应的参数的水平取值,得到最优参数组合。
10) 判断所述步骤9的最优参数组合中各参数的水平取值是否满足精度需求,即
(
为染色体
中第i + 1个方案对应的第j个参数的取值,
为精度),如果满足,则停止计算,所述步骤9得到的最优参数组合作为最终计算结果;否则重复步骤2~9,直到满足精度需求。
5. 具体算例
以我国南方地区酉水流域凤滩水库为例,验证所提方法的有效性。该流域为亚热带季风气候,流域面积为1.7万km2,平均温度18摄氏度。3~7月的降雨占全年的65%以上,雨量充沛,降雨集中,中长期径流预报难度较大。流域内的预报降雨与蒸发数据根据流域内的27个气象站,采用泰森多边形计算得到。本次计算选取2000年1月~2018年12月共计18年的103场降雨数据进行参数率定,以2019年1月到2020年12月的19场洪水进行校核。
采用本文所提方法对新安江三水源模型进行参数校核,算例中遗传算法的初始种群规模为200,交叉概率为0.65,变异概率为0.05,进化代数为500代,计算终止条件
,所有仿真程序均用java语言编写,运行环境为4核CUP、主频3.2 GHZ、内存为16 GB、硬盘500 GB、Windows系统的ThinkPad计算机。为了保证计算结果的合理性,计算5次,计算结果如表1所示:

Table 1. The calculation results of the proposed method in this paper
表1. 本文所提方法计算结果
取最优计算结果,模型各个参数如表2所示:

Table 2. Parameter calibration results of Xin’anjiang Model
表2. 新安江模型参数率定结果表
根据表1可以看出,遗传算法5次计算结果不一致,原因是遗传算法由于交叉与变异概率的随机性。取最优计算结果,其洪峰流量的合格率为84.46%,洪量的合格率为93.20%,峰现时间的合格率为86.41%。对参与校核的19场洪水进行分析,其洪峰流量的合格率为78.64%,洪量的合格率为89.47%,峰现时间的合格率为94.74%,本文所提方法洪峰、洪量、峰现时间合格率均大于70%满足乙级标准。
为了进一步验证并行算法的并行计算性能,将并行遗传算法与串行遗传算法进行对比分析。测试基于并行核数与终止条件
进行分析,并采用衡量并行算法的两个重要指标来评价加速比
与效率
来测试并行遗传算法的性能,其中
与
分别采用下式计算:
(8)
式中:
为串行遗传算法计算一次所需要的时间,
为并行遗传算法计算所需时间,C为并行遗传算法中的并行核数。
由表3可知,串行遗传算法非常耗时,且随着离散精度的不断减少所需时间不断增加,当离散精度为
时,串行遗传算法所需时间为156分钟(9356 s),无法满足时效性的要求,相同离散精度下,采用并行遗传算法可大大缩短计算时间,在所实验的范围内,参数率定所需要的时间随着并行核数的增加而减少。当离散精度为
,2核环境下所需的时间为4873 s,大约是串行时间的一半;在16核的环境下,仅需824 s即可完成计算。因此并行遗传算法可有效提高参数率定速率,是改善大规模复杂问题的一个切实可行的方法。在两核环境下,离散精度从
依次到
,加速比从1.82到1.92,效率由0.91增加到0.96;并且随着并行核数的增多,加速比与效率随着离散精度的提高而更加明显。

Table 3. Calculation results under different parallel environments
表3. 不同并行环境下的计算结果
6. 结论
本文探讨了基于并行遗传算法的新安江模型参数率定方法,充分利用了遗传算法天然可并行的优势,采用并行计算,多核计算机的计算特性,极大地提高了计算速度,参数率定准确率达到乙级标准。但本文未解决遗传算法容易陷入局部最优的问题,且算法的稳定性没有确切的数据说明,这在以后的参数率定中需要进一步完善。
参考文献