1. 引言
研究气候变化对水文水资源的影响,常常采用降尺度方法将GCM输出与水文模型输入有效地衔接起来 [1]。其中,偏差校正方法是最重要的降尺度方法之一,被广泛地应用于气候变化影响评估中 [2] [3] [4]。偏差校正方法均基于GCM输出变量(如降水和气温)偏差一致性的假设,即假设GCM输出变量的偏差在历史和未来时段相同。但是,最新的一些研究 [5] [6] [7] 表明气候模式输出变量的偏差并不是恒定不变的,即具有非一致性。GCM输出变量偏差的非一致性主要归因于两个部分,即气候内部变率和气候模式敏感性。随着人们对气候系统的深入认知,气候模式的结构将更加完善,不同气候模式在相同温室气体排放情景下的响应将更加准确和趋于统一。因此,气候模式敏感性会随之而逐渐减弱甚至消除。同时,偏差校正方法的不断发展也会在一定程度下消除气候模式敏感性的影响。然而,由于气候是一个典型的非平稳系统,气候本身具有难以预计的周期性和趋势性变化,气候内部变率是无法消除和忽略的。因此,气候内部变率所引起的偏差非一致性对偏差校正结果的影响无法完全消除。也就是说,在气候内部变率的影响下,偏差校正方法无法完全消除气候模式输出变量的偏差。
本文的主要目的就是考虑在气候内部变率的影响下,如何合理和正确地评价偏差校正方法的结果。首先,基于气候模式多成员集合,估算气候内部变率。随后,对气候模式输出变量的模拟值进行偏差校正,将检验期或未来时段内的残留偏差(偏差校正值与观测值之前的差异)和气候内部变率比较,评价偏差校正结果的合理性。如果检验期的残留偏差在气候内部变率的范围内,则认为偏差校正的结果是较为准确和合理的,可以进一步用于气候变化影响研究。此外,由于气候内部变率是偏差校正评价方法的评价基准,气候内部变率模拟值的不同,则会直接影响着评价方法的结果。本文进一步研究了气候内部变率模拟值的不确定性对评价方法结果的影响。
2. 偏差校正评价框架介绍
在气候模式输出变量偏差的非一致性的基础上,建立了以气候内部变率为基准的偏差校正评价框架 [8],如图1所示。该评价框架主要包含3个步骤:1) 估算气候内部变率;2) 构建观测值范围;3) 以气候内部变率为评价基准来评估偏差校正后GCM输出降水、最高和最低气温的残留偏差。
气候内部变率基于同一气候模式的多成员集合来估算,具体方法如下:1) 在同一时段内,分别计算每个成员的气候变量序列的统计指标(如均值、95%分位数等);2) 在同一时段内,计算不同成员间气候统计量的变化范围(最大值减去最小值),将其作为气候内部变率的范围。
近现代所观测到的气候变化序列其实仅仅是气候的许多可能性的一种。但是,观测序列是这些可能发生的气候序列中具体哪一个却不得而知。同时,相对于这些可能发生的气候序列的中位数来讲,也无法确定观测序列是偏低、偏高还是相等。如果观测序列是可能性中的最低值,则所有可能发生的气候序列在高于观测值的1个单位气候内部变率的范围内。如果观测序列是可能性中的最高值,则所有可能发生的气候序列都在低于观测值的1个单位气候内部变率的范围内。因此,所有可能发生的气候序列最大变化范围是在高于和低于观测值的1个单位气候内部变率之间。在气候内部变率的影响下,可能发生的气候序列的范围(Range)是:
(1)
式中,obs为观测值,ICV为一个单位的气候内部变率。
依据气候内部变率影响下的气候序列变化范围,偏差校正后的结果可以得到合理的评价。如果当偏差校正后的残留偏差(Remaining Bias,RB)在气候内部变率的范围内,即
,则认为气候模式输出变量在偏差校正后无明显偏差,即偏差校正达到了预期效果。如果残留偏差超出了气候内部变率的范围,即
或
,则认为偏差校正后有明显的残留偏差,即偏差校正不能完全或很好的消除气候模式输出变量的偏差。

Figure 1. Diagram of the framework to consider internal climate variability for bias correction methods
图1. 考虑气候内部变率影响的偏差校正评价框架结构示意图
3. 评价框架应用
3.1. 研究区域与数据
渭河流域位于中国西北黄土高原的东南地区,地理位置在33˚40'~37˚26'N,103˚57'~110˚27'E之间,流域总面积为13.48万km2。本文选取华县站以上部分流域作为研究区域,集水面积为10.65万km2。
研究数据包括流域气象观测数据和GCM数据。气象观测数据主要包含渭河流域内及周边气象站的1961~2014年逐日降水、最高和最低气温历史观测数据。GCM数据主要包括气候模式多成员集合数据和多气候模式集合数据,见表1。其中,气候模式多成员集合数据主要包括4个GCMs的多成员集合,即CanESM2的50个成员集合,CESM1的40个成员集合,CSIRO-MK3.6.0的10个成员集合以及IPSL-CMA-LR的4个成员集合。多气候模式集合数据主要包括13个气候研究中心的22个GCM,GCM数据来源于耦合模式比较计划第五阶段(CMIP5) GCM数据集,如表2所示。GCM数据时间跨度为1850~2100年,其中,历史时段为1850~2005年,情景时段为2006~2100年,温室气体排放情景选用的是RCP8.5。

Table 1. General information of the 22 chosen GCMs
表1. 22个GCM的基本信息
3.2. 气候内部变率的评估
气候模式多成员集合是指基于不同的初始条件多次运行某一气候模式生成相同辐射强迫下的多种气候模拟序列。各成员间在模式结构、外部强迫和气候模式敏感性等方面相同,但具有不同的初始条件,因此各成员的差异可以代表气候内部变率。因此,本文采用同一气候模式的多成员集合来估算气候内部变率。例如,在一定时段内,一个气候模式的m个成员的气候统计变量(见表2)为
,则气候内部变率的估算公式如下:
(2)
式中,上标t为计算的时间段;下标
为气候模式;
为在时段t内气候模式的第m个成员在该时段内的气候统计量,例如,
为在1961~1980年内CanESM2多成员集合中的第1个成员的气候统计量;
为在时段t内根据选取的气候模式多成员集合估算的气候内部变率。由于气候内部变率是基于同一个时段来估算的,为了考虑其随时间是否变化,本节中在多个时段内估算了气候内部变率。在本节中,以20年为滑动窗口、1年为步长将1950~2100年共151年分为了132个时段。例如:1950~1969 (1960 s),1951~1970 (1961 s),1952~1971 (1962 s),……,2081~2100 (2091 s)。进而,分别在132个时段内估算了气候内部变率。
为了研究气候内部变率模拟值的不确定性对偏差校正评价结果的影响,即不同气候模式的多成员集合估算得到的气候内部变率的不同,本文针对CanESM2的50个成员集合(
)、CESM1的40个成员集合(
)、CSIRO的10个成员集合(
)和IPSL的4个成员集合(
)分别估算气候内部变率。通过比较不同气候模式多成员集合的估算结果,来分析气候内部变率模拟值的不确定性。
3.3. 历史时段的应用
本文中采用的偏差校正方法是DBC方法,该方法的具体步骤可以参见Chen等 [9]。本文选取了1961~2014年的观测的和22个GCMs模拟的日降水、最高和最低气温。同时,将观测和模拟数据分别率定期和检验期,其中,率定期是1961~1980年,检验期是1981~2000年。针对22个GCMs模拟值,分别进行DBC偏差校正,得到偏差校正结果。随后,以气候内部变率为评价基准,评价偏差校正结果,即残留偏差指标RI (Remaining Bias Index),具体公式如下:
(3)
式中,RB为偏差校正后的残留偏差(偏差校正值减去观测值);ICV为气候内部变率。RI是基于在同一时段内的RB和ICV的计算结果。当RI为0时,则认为偏差校正后没有明显偏差;当RI不为0时,则认为偏差校正后有明显偏差,且偏差是RI个单位的气候内部变率。本文根据不同气候模式的气候内部变率估计值,即
、
、
和
,分别计算对应的RI值。
3.4. 未来时段的应用
本文以气候内部变率为基准的偏差校正评价框架在未来时段做进一步应用。由于无法获得未来时段的观测值,因此采用气候模式的模拟值作为虚拟观测值来代替未来实际观测值 [6] [10]。本文使用的数据包括1950~2100年的22个GCMs模拟的日降水、最高和最低气温。将22个GCMs轮流作为虚拟观测值,对其余GCMs模拟值进行偏差校正,得到偏差校正后的残留偏差。总共可以得到无重复的231 (
)种组合。
在每种组合中,均采用DBC偏差校正方法来进行偏差校正。其中,率定期为1950~1969年(1960 s),而检验期选取了未来的4个时段,即2020~2039年(2030 s)、2040~2059年(2050 s)、2060~2079年(2070 s)和2080~2099年(2090 s)。随后,以气候内部变率为基准,计算偏差校正后的RI值,计算公式为公式(3)。由于每种组合的虚拟观测值和模拟值之间是可以相互交换的,因此,在计算每种组合的残留偏差以及RI值时,都采用绝对值。
3.5. 评价指标
为了较为全面的评价偏差校正的结果,采用16种气象统计量作为评价指标,具体信息见表2。针对这16种评价指标,分别计算了他们在历史时段和未来时段的气候内部变率和RI值。

Table 2. The definition of evaluation index for the precipitation, maximum and minimum temperature
表2. 降水、最高和最低气温的评价指标名称及其定义
4. 结果分析
4.1. 气候内部变率的评估结果
图2展示了渭河流域的降水、最高和最低气温的日均值气候内部变率的估算结果。从图中可以看出,采用不同的气候模式多成员集合,所得到的气候内部变率有比较大的差异。总体来说,气候模式的成员越多,估算的气候内部变率值越大。例如,对于日平均降水量,
。此外,气候内部变率在时间上也发生着变化。气候模式成员越多,其估算的气候内部变率随时间的波动范围相对越小。因此,选用成员较多的气候模式多成员集合,其估算的气候内部变率更稳定。虽然气候内部变率随时间发生变化,但是其变化范围远远小于气候内部变率模拟值的不确定性,即不同气候模式多成员集合估算的气候内部变率间的差异。例如,渭河流域的日降水
在0.7 mm到1.1 mm之间波动,而不同气候模式估算的气候内部变率的范围在0.7 mm左右。
4.2. 偏差校正评价框架在历史时段的应用结果
图3展示了历史时段GCMs模拟降水在偏差校正前、后的残留偏差指数(RI)结果。其中,白色表示偏差小于气候内部变率,即认为没有明显偏差,而红色或蓝色表示偏差超出气候内部变率范围,即认为存在明显偏差。从图中第一和三列可以看出,虽然每个GCM模拟的降水偏差有些差异,但是其在率定期和检验期均存在明显的
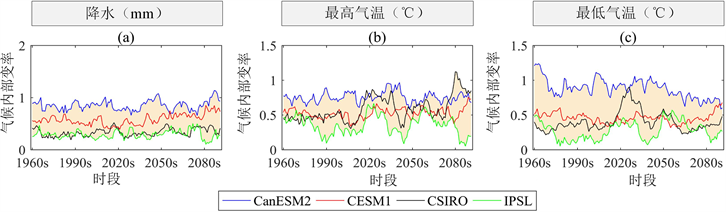
Figure 2. The results of internal climate variability for the daily precipitation, maximum and minimum temperature
图2. 流域降水、最高和最低气温的日均值气候内部变率结果图

Figure 3. The Remaining Bias Index (RI) of the raw and bias-corrected precipitation of 22 GCMs over historical period
图3. 历史时段22个GCMs模拟降水在偏差校正前、后的残留偏差指数(RI)图
高估现象。在经过偏差校正后,GCM模拟降水偏差得到了有效的降低,且残留偏差大部分在气候内部变率内,即RI值等于0。第二和四列展示了GCM偏差校正后的残留偏差以气候内部变率为基准计算得到的RI值。残留偏差RI值在率定期内基本为0,但是在检验期内,一些GCMs在个别评价指标上的残留偏差RI值出现了不等于0的情况。该情况表明,偏差校正方法在历史时段能够有效降低GCM模拟降水偏差,但是,偏差的非一致性对偏差校正结果在一定程度上产生了影响,使得偏差校正结果在检验期的表现差于率定期。此外,以不同的气候内部变率为基准计算得到的RI值有着明显的区别。对于GCMs偏差校正前、后的RI值,均表现出了气候模式的成员越多,以其估算的气候内部变率为基准计算得到的RI值越小。例如,在第一列中,从上到下红色明显增多,表明
和
明显小于
和
。在第二列中,
和
都为0,有1个GCM在5%分位数上的残留偏差
略微大于0,而15个GCM在5%分位数上的残留偏差
大于或小于0。
图4展示了历史时段渭河流域GCMs模拟最高气温在偏差校正前、后的残留偏差指数结果。从图中可以看出,在偏差校正前,大部分GCMs模拟的最高气温的RI都小于0,表明最高气温被明显低估。但是,一些GCMs (如,ACCESS1.0、CNRM-CM5和MIROC5等)在95%分位数、8~12月等评价指标上的RI值大于0,表明最高气温被高估。经过偏差校正后,GCM模拟最高气温偏差得到了有效的降低。在率定期内,GCM校正值与观测值之间的偏差都在气候内部变率以内,RI值等于0。在检验期内,大部分GCMs残留偏差在气候内部变率以内。但是,以不同的气候内部变率为基准,计算得到的RI值有明显的差异。图4(d)是以
为基准计算的RI值,
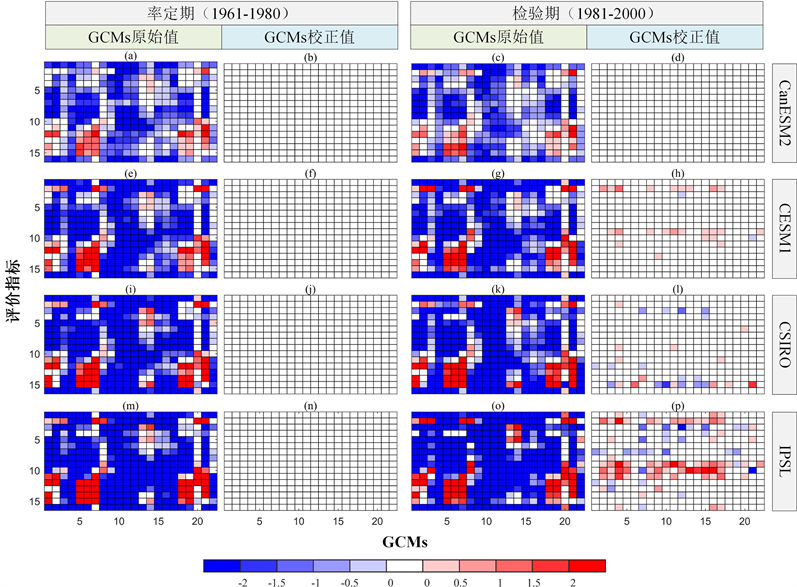
Figure 4. The Remaining Bias Index (RI) of the raw and bias-corrected maximum temperature of 22 GCMs over historical period
图4. 历史时段22个GCMs模拟最高气温在偏差校正前、后的残留偏差指数(RI)图
图中显示在检验期最高气温经过偏差校正后没有明显的偏差(RI = 0)。然而,成员数量越少的气候模式多成员集合,所对应的RI值越明显。尤其是在图4(p)中,以
计算的RI值不等于0的个数明显大于其他的气候变率计算得到的RI值。这是由于各评价指标的
整体偏小,使得更多的残留偏差超出了气候内部变率的范围。但是,并不是每一个评价指标的
都是最小。例如,8月份最高气温的
比
大,表现的结果是前者对应的RI值为0而后者对应的RI大部分都不为0。另外,最低气温和最高气温结果相似。
4.3. 偏差校正评价框架在未来时段的结果
图5所示展示了未来时段GCMs模拟降水在偏差校正前、后与虚拟观测值之间的偏差结果图。第1和2列为偏差校正前后,231种组合的RI的平均值。第3和4列为偏差校正前后,RI值大于0的组合数占总组合数的百分比。从图中可以看出,在率定期内,GCMs模拟的降水与虚拟观测值之间有明显的偏差,且气候模式成员越少的RI值越大。例如,
在0到0.6之间,
在0.1到1.3之间,
在0.5到4.3之间,
在0.2到7.2之间。在偏差校正后,率定期的RI值基本为0,表明偏差校正方法有效的降低了GCM模拟降水偏差。在未来时段,GCMs模拟值与虚拟观测值之间仍然具有较大的偏差。经过偏差校正后,虽然RI值整体减小,但是依然大于0,表明在未来时段偏差校正后的残留偏差依然很大。本文采用虚拟观测方法共组成了231种组合,第3和4列统计了这些组合中RI值大于0的占比(PRI)。占比越大,表明越多组合计算得到的偏差是明显的。从
可知,超过50%的组合在日降水、95%分位数和年降水等评价指标上具有明显的偏差,而月尺度的评价指标上,有8%到49%的组合具有明显的偏差。对于成员越少的气候模式多成员集合,PRI越高。例如,
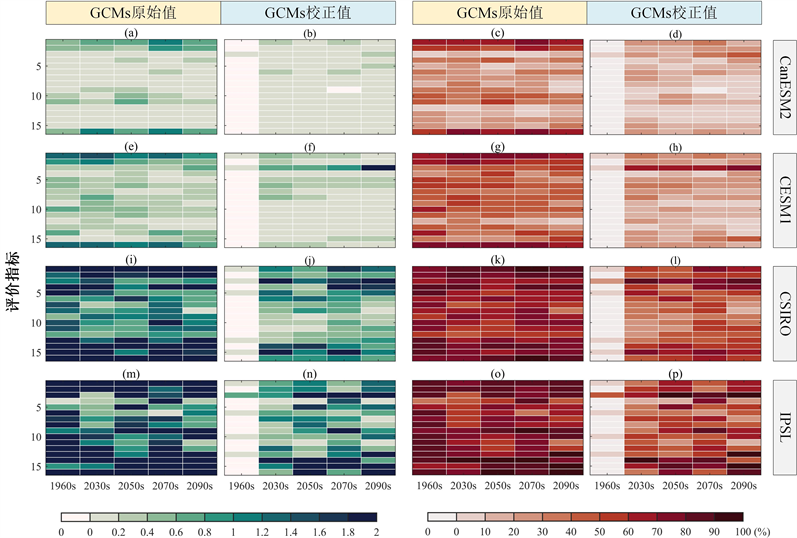
Figure 5. The Remaining Bias Index (RI) of the raw and bias-corrected precipitation of 22 GCMs over future period
图5. 未来时段22个GCMs模拟降水在偏差校正前、后的残留偏差指数(RI)图
在36%和97%之间。在率定期,偏差校正后的PRI有了明显减小,在大部分评价指标上都为0。在未来时段,PRI虽然在一定程度上变小,但是依然有较多的组合RI大于0,存在明显的偏差。例如
在12%到93%。这表明,偏差校正方法在未来时段无法有效降低GCM模拟降水的偏差。
图6展示了未来时段渭河流域GCMs模拟最高气温在偏差校正前、后与虚拟观测值之间的偏差结果图。从图中可以看出,无论是率定期还是未来的检验期,GCMs模拟的最高气温与虚拟观测值之间都具有明显的偏差。从整体上看,
是0.86,
是1.62,
是1.73,
是3.97。经过偏差校正后,率定期的RI值降到0,表明偏差校正方法有效降低了GCM模拟最高气温偏差。在未来时段,虽然RI值有所减小,但是仍旧明显大于0。例如,
是0.37,
是0.76,
是0.80,
是2.34。从PRI上来看,GCM模拟最高气温偏差中大于0的组合都超过了50%。例如,
是62%,
是72%,
是74%,
是82%。在率定期内,偏差校正后PRI为0。在未来时段,虽然偏差校正后PRI有所减小,但依然较大。例如,
是42%,
是57%,
是58%,
是70%。这表明,偏差校正方法在未来时段的无法有效降低GCM模拟最高气温的偏差。另外,最低气温和最高气温结果相似。
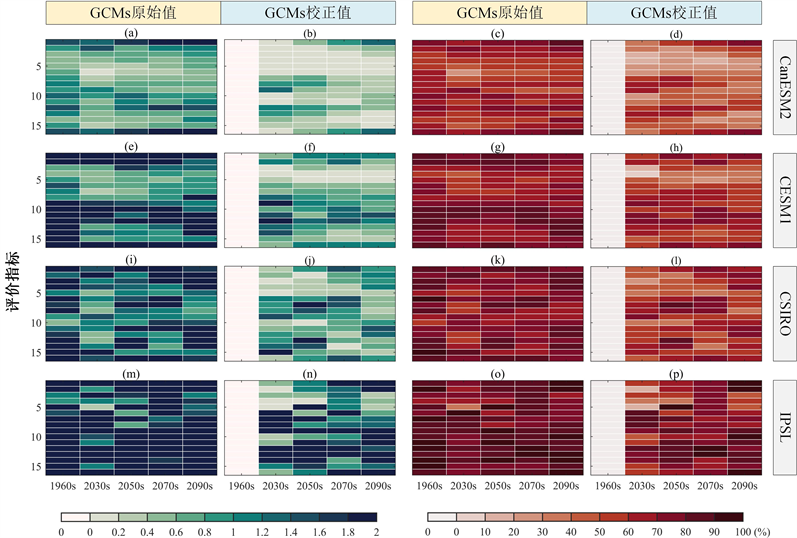
Figure 6. The Remaining Bias Index (RI) of the raw and bias-corrected maximum temperature of 22 GCMs over future period
图6. 未来时段22个GCMs模拟最高气温在偏差校正前、后的残留偏差指数(RI)图
5. 结论
由于气候是一个典型的非平稳系统,气候本身具有难以预计的周期性和趋势性变化,气候内部变率是无法消除和忽略的。因此,本文建立了以气候内部变率为基准的偏差校正评价框架。该评价框架的理论依据是:当校正值与观测值之间的偏差(即残留偏差)在气候内部变率范围内,则认为偏差校正达到了预期的目的;反之,则认为偏差校正不能很好地消除气候模式输出变量的偏差。然后,采用该评价框架评估了偏差校正方法在历史和未来时段的偏差校正结果。在未来时段,由于没有实际观测数据,所以采用GCMs数据作为虚拟观测值进行分析。同时,本文分别通过4个气候模式多成员集合估算了气候内部变率,进而分析气候内部变率模拟值的不确定性对偏差校正评价结果的影响。主要结论如下:
1) 不同气候模式多成员集合估算的气候内部变率具有明显的不确定性,其中,CanESM2估算的气候内部变率最大,IPSL估算的气候内部变率最小。同时,气候内部变率还随着时间发生了一些变化,但是这些变化远远小于气候内部变率模拟值的不确定性。
2) 采用以气候内部变率为基准的偏差校正评价框架,评价偏差校正方法在历史时段的偏差校正效果,结果表明:在检验期,偏差校正方法整体上能够有效地降低GCMs偏差,使得偏差校正后的残留偏差在气候内部变率范围内。但是,少数GCMs校正后的残留偏差超过了以IPSL和CSIRO估算的气候内部变率范围。
3) 采用以气候内部变率为基准的偏差校正评价框架,评价偏差校正方法在未来时段的偏差校正效果,结果表明:偏差校正方法在率定期能够有效地降低GCMs偏差,使得校正后的残留偏差在气候内部变率范围内。但是在未来时段,偏差校正方法仅仅在一定程度上降低了GCM输出变量的偏差。虽然基于不同GCM多成员集合估算的气候内部变率具有明显的不确定性,但残留偏差依然可能大于气候内部变率。
基金项目
受湖北省自然科学基金青年项目(2021CFB152和2020CFB327)和重庆市自然科学基金面上项目(cstc2021 jcyj-msxm2426)资助。