1. 引言
城市地铁隧道无法避免下穿既有建筑物,而隧道开挖会影响上部建筑物的安全性,严重时会造成建筑物倒塌或者减少其使用寿命。因而当地铁隧道下穿建筑物时,需要分析对上部建筑的影响。朱逢斌等 [1] 通过建立三维弹塑性有限元模型,研究地铁隧道的开挖对上部桩基和地表沉降的影响。何历超等 [2] 采用有限元分析方法进行数字模拟仿真,对两种不同工况的地表沉降进行了研究。程邦富等 [3] 对地铁暗挖施工对既有建筑的影响进行研究,采用有限元软件对其进行仿真研究。肖博等 [4] 采用FLAC3D建立相关的模型对隧道开挖后地表建筑物的变形和受力进行了相应的分析。王丽等 [5] 采用ABAQUS建立三维有限元模型模拟隧道下穿位置对建筑物框架结构的影响。田明杰 [6] 采用强度折减法对隧道以及隧道下穿既有城市道路近接体系的稳定性进行分析。但以上分析大多采用荷载结构法、等效荷载法,未采用地层结构法进行分析研究,地层结构法可以充分考虑地下结构与周围地层的相互作用,根据具体的施工过程可以充分模拟地下结构以及周围地层在每一个施工工况下的结构内力和地层的变形。本文基于地层结构法,采用MIDAS有限元软件分析,结合Peck公式预测地表沉降量,研究重庆地铁18号线某区间隧道施工对上部建筑的影响。本文研究结果可为类似工程案例提供参考。
2. 工程概况
富华路站~歇台子站区间为重庆18号线工程由北向南的第1个正线区间,区间隧道下穿重庆总部城A区10号建筑物,隧道左右线均下穿该建筑物,位置关系如图1所示。隧道开挖宽度为7.02 m,开挖高度为6.78 m,双线净距为8.14 m。隧道下穿的建筑物为钢筋混凝土框架结构,地上5层,地下1层,层高3 m,竖向距隧道拱顶约94.7 m。
 (a) 平面位置关系
(a) 平面位置关系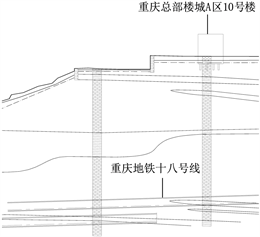 (b) 竖向位置关系
(b) 竖向位置关系
Figure 1. Location relationship between tunnel and building
图1. 隧道与建筑位置关系
隧道采用复合式衬砌,其中初期支护为C25喷射混凝土层,厚度为220 mm,预留变形量50 mm,内设锚杆长度L = 2.5 m @ 1.2 × 1.2 m梅花形布置,钢架采用I14工字钢,间距为1.2 m,以及钢筋网φ 8 @ 200 × 200 mm;二次衬砌采用钢筋混凝土结构,混凝土为C40,厚度为350 mm。隧道采用全断面开挖,每循环开挖进尺不大于2 m,隧道断面形状及开挖步骤如图2所示。
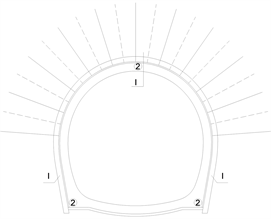 (a) 区间隧道横断面图
(a) 区间隧道横断面图 (b) 区间隧道纵断面图
(b) 区间隧道纵断面图
Figure 2. Tunnel excavation steps
图2. 开挖步骤
3. 有限元计算分析
为研究重庆地铁18号线隧道开挖对上部建筑的影响,本文采用MIDAS GTS NX有限元分析软件模拟分析隧道开挖时隧道拱顶沉降量、地表面沉降值以及建筑物整体倾斜度。
3.1. 模型参数
模型在隧道截面的横向方向,左右各取3倍的开挖宽度;在隧道截面的竖向方向,隧道底部往下取3倍的开挖高度;隧道顶部取至地表。土层的材料采用德鲁克-普拉格本构模型,以考虑围岩的非线性变形,岩土体力学参数见表1。初期支护中喷射的混凝土层采用梁单元,锚杆采用植入式桁架单元;隧道围护结构材料力学参数见表2所示。计算模型如图3所示。

Table 1. Physical and mechanical parameters
表1. 岩土物理力学参数

Table 2. Physical and mechanical parameters of tunnel structure
表2. 隧道结构材料物理力学参数
3.2. 结果分析
首先计算原始地应力,岩土体的开挖是在前一计算步骤所得地应力分布的基础上进行的,根据结构整体刚度的改变,按全断面法开挖地层并逐步释放荷载,最终求解开挖后的应力场。其中初期支护根据平面应变理论,采用地层结构法进行分析,通过设置释放系数控制初期支护的受力,开挖过程中应力释放40%,初期支护承担60%的荷载。
隧道开挖并支护完成后,初期支护内力如图4所示,锚杆最大轴力为30.7 kN,从锚杆轴力图可以看出,锚杆轴力均在其抗力强度范围内,区间隧道开挖支护后初支的最大弯矩值21.1 kN·m,最大轴力值为1494.0 kN,最大剪力值为210.3 kN,安全系数为2.77 (抗压控制),计算结果表明初期支护设计参数满足受力要求。
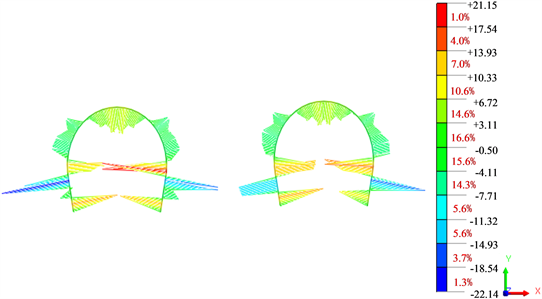 (a) 初支弯矩图(单位:kN·m)
(a) 初支弯矩图(单位:kN·m) (b) 初支轴力图(单位:kN)
(b) 初支轴力图(单位:kN)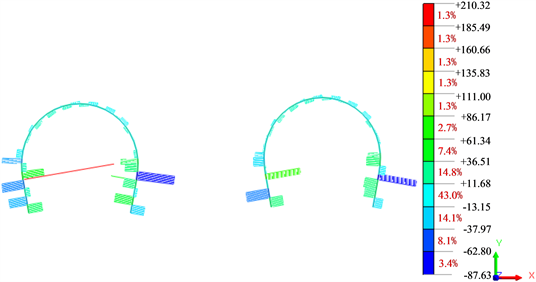 (c) 初支剪力图(单位:kN)
(c) 初支剪力图(单位:kN)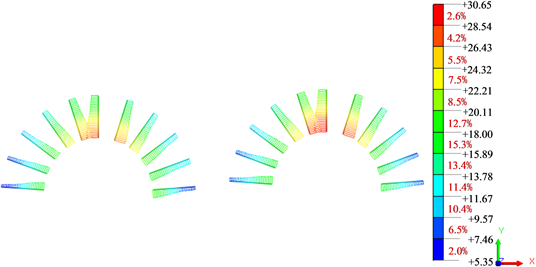 (d) 锚杆轴力图(单位:kN)
(d) 锚杆轴力图(单位:kN)
Figure 4. Internal force diagram of primary support
图4. 初期支护内力图
由图5可知,隧道开挖完成后,区间隧道支护后最大的竖向位移值为:左线拱顶为−5.51 mm,底板隆起值为+3.10 mm;右线拱顶为−5.59 mm,底板隆起值为+2.93 mm,隧道拱顶及地表面沉降满足要求。隧道支护后最大的水平位移值为:左线左侧向洞内变形1.08 mm,右侧向洞内变形−1.07 mm;右线左侧向洞内变形1.24 mm,右侧向洞内变形−1.18 mm,满足收敛要求,开挖支护后围岩稳定性较好。
由图5可知,隧道下穿建筑物整体最大沉降为1.85 mm,相邻基础最大差异沉降为:1.85 − 1.85 = 0 mm < 8 mm,满足变形控制标准。建筑整体倾斜为:(1.85 − 1.85)/33068.4 (建筑物横向宽度) = 0 < 0.002,满足变形控制标准。
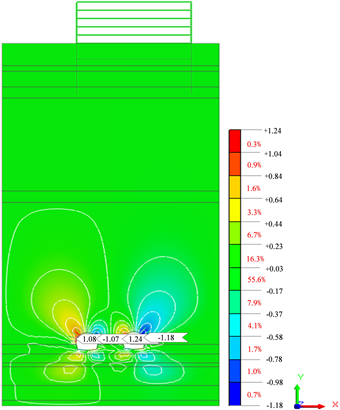 (a) 竖向位移(单位:mm)
(a) 竖向位移(单位:mm) (b) 水平位移(单位:mm)
(b) 水平位移(单位:mm)
Figure 5. Displacement nephogram
图5. 位移云图
4. Peck公式沉降预测计算
在有限元计算的基础上,采用Peck公式进行沉降预测计算。Peck在分析大量地表沉降观测数据的基础上提出地表沉降槽符合正态分布曲线,地表沉降分布曲线计算公式见式(1) [7]:
(1)
式中,y为距离隧道中心线为x处的地表沉降值。Smax为隧道中心线处地表最大沉降值,计算公式见式(2) [8];i为沉降槽宽度系数,计算公式见式(3) [9]。
(2)
式中,Vl为地层损失率,取值主要与工程地质情况、水文地质情况、隧道施工方法、施工技术水平以及工程管理经验等因素相关。D为隧道直径,对于类圆形隧道(如椭圆隧道、公路隧道、断面常用的量同心圆或三同心圆隧道等),可采用等效大圆模型 [10]。
(3)
式中,Z0为隧道埋深,K为沉降槽宽度参数,主要取决于岩土体特性。
对于平行修建的双线隧道,利用叠加原理,即可得到双线隧道Peck公式 [10]。该工程隧道埋深Z0取94.7 m,对于砂质泥岩地层,沉降槽宽度参数K可取0.5~0.7,地层损失率取Vl取0.8~1.8 [10],隧道直径按D取7.02 m的圆形隧道计算。
由式(1)~(3)计算可得隧道左或右线正上方的地表沉降量在0.37 ~1.16 mm,隧道左右线中心点正上方的地表沉降量在0.37~1.17 mm,建筑物角部地表沉降量在0.36 ~1.07 mm之间,如图6所示。Peck公式预测的地表沉降量比MIDAS GTS NX有限元计算的值小,最大沉降量相对误差约为−37%,两者在定性上较为吻合。由此可知,邻基础最大差异沉降约为0.1 mm < 8 mm,满足变形控制标准。建筑整体倾斜为:0.1/24140 mm (隧道中心线至建筑物角部距离) = 0 < 0.002,满足变形控制标准。
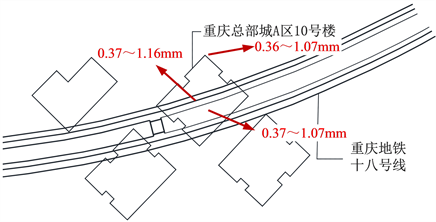
Figure 6. Distribution of building settlement
图6. 地表建筑物沉降分布曲线
5. 结论
本文以重庆市地铁18号线某暗挖段隧道为研究背景,基于地层结构法有限元分析和Peck公式沉降预测分析了隧道施工对上部建筑结构的影响,得到了以下结论:
1) 隧道拱顶最大沉降为5.59 mm,水平位移最大为1.24 mm,且初期支护结构设计参数满足受力要求;
2) 有限元模拟分析表明,重庆总部城A区10号楼建筑物整体沉降最大值1.85 mm,差异沉降最大值为0,整体建筑没有发生倾斜。
3) Peck公式预测地表最大沉降量约1.17 mm,与有限元模拟分析结果在定性上较为一致,建筑物地表沉降差最大值为0.01 mm,建筑物自身可以抵抗隧道开挖的影响。