MATLAB融入线性代数教学的实践与思考

期刊菜单

MATLAB融入线性代数教学的实践与思考
Practice and Thinking of Integrating MATLAB into Linear Algebra Teaching

DOI: 10.12677/CES.2021.94150, PDF,
作者: 鞠桂玲, 胡红娟：陆军装甲兵学院基础部数学教研室，北京
关键词: 线性代数；MATLAB；仿真实现；Linear Algebra； MATLAB； Simulation Implementation

摘要: 文章结合线性代数的特点及存在的问题，探讨了把MATLAB软件融入线性代数教学的必要性和优势，结合具体内容介绍了软件的应用，为MATLAB软件更好地应用于线性代数教学提供了参考。

Abstract: Combined with the characteristics and existing problems of linear algebra, this paper discusses the necessity and advantages of integrating MATLAB software into linear algebra teaching, and in-troduces the application of the software combined with the specific content, which provides a ref-erence for the better application of MATLAB software in linear algebra teaching.

文章引用：鞠桂玲, 胡红娟. MATLAB融入线性代数教学的实践与思考[J]. 创新教育研究, 2021, 9(4): 908-913. https://doi.org/10.12677/CES.2021.94150

1. 引言

线性代数是高等院校理工科专业的一门重要基础课程，是后续专业课程的数学基础。对于学生逻辑推理能力、抽象思维能力和基本运算能力，以及用数学方法解决实际问题的能力的培养有着重要意义。然而，现在使用的线性代数教材，理论性比较强，学生在学习过程中，普遍感觉这门课程比较抽象，有些问题难于理解，学习的主观意愿比较低，同时，实际问题涉及的变量往往很多、数字繁琐，庞大的数据处理和复杂的运算步骤使得计算既费时又容易出错，学生不容易动手计算完成，这就使得这门课程的教学方法、教学手段等的改革势在必行。随着计算机技术的发展，尤其是数据处理软件的日渐成熟，使复杂繁琐的计算可以快速地完成，利用MATLAB仿真软件来处理线性代数问题，可以达到事半功倍的效果。

2. MATLAB的特点及在线性代数教学中的意义

MATLAB是matrix与laboratory的缩写，是由Cleve Moler在Linpack和Eispack软件实验室中开发的，多年来MATLAB经历了一系列的扩展和改版，逐渐地发展成通用科学计算、图示交互系统和程序设计语言，在线性代数中有着非常广泛的应用。除了它自带的工具箱外，还可以根据需要，建立相应的Ｍ-文件，解决更加复杂的问题，使人们从繁重的手工计算和高级语言程序调试中彻底解脱出来 [1]。

将MATLAB应用于线性代数课程教学，一方面，可以借助MATLAB讲解有关定义和定理，使理论知识具体化、形象化，进一步加深学生对基本概念和定理的理解，激发学生的学习兴趣。同时，由于低维问题具有形象的几何意义，通过图形能强化学生的感性认识，因此，在教学中，教师可以以低维问题为基础，借助MATLAB数学软件，帮助学生理解一些抽象的概念，实现由具体到抽象的思维过程。另一方面，能有效扩大线性代数应用实例的范围，有助于学生完成与实际有关的大型问题的数学建模，让学生感觉到学有所用的同时，强化自己的应用意识，培养运用所学内容解决实际问题的应用能力。

3. MATLAB在线性代数教学中的应用

下面举例说明MATLAB在线性代数教学中的应用。

3.1. 借助MATLAB软件理解定理，激发学生学习兴趣

线性方程组的解有以下定理 [2] ：

对于n元线性方程组 $Ax = b$ ；

1) 无解的充分必要条件是 $R (A) < R (A, b)$ ；

2) 有唯一解的充分必要条件是 $R (A) = R (A, b) = n$ ；

3) 有无限多解的充分必要条件是 $R (A) = R (A, b) < n$ 。

学习过程中，很多学生不理解线性方程组的不同情况解的意义，感觉定理内容比较抽象，不好理解。由于二元、三元线性方程分别表示直线和平面，可以借助Matlab绘图帮助学生理解线性方程组解的含义。例如，求包含两个变量的两个线性方程组成的方程组的解，等价于求两条直线的交点问题。

针对以下方程组

a) ${\begin{cases} x {}_{1}- 2 x_{2} = - 1 \\ - x {}_{1}+ 3 x_{2} = 3 \end{cases}$ ，b) ${\begin{cases} x {}_{1}- 2 x_{2} = - 1 \\ - x {}_{1}+ 2 x_{2} = 3 \end{cases}$ ，c) ${\begin{cases} x {}_{1}- 2 x_{2} = - 1 \\ - x {}_{1}+ 2 x_{2} = 1 \end{cases}$

根据解的判定定理，三个方程组解的情况，分别是有唯一解，无解，无穷多解。

三个方程组对应的图形见图1，通过图形可以直观的看到方程组的解的几何含义，方程组有唯一解、无解、无穷多解分别对应于两直线相交、平行、共线。借助Matlab数学软件，对低维问题有了直观的几何形象感知之后，可以把这个结论推广到高维的情形，实现由具体到抽象的思维的培养。

(a) (b) (c)

Figure 1. Geometry of equations

图1. 方程组的几何图形

3.2. 借助MATLAB软件化抽象为具体，增加问题的直观性

关于二次型有下面的定理 [3]

定理1. 任给二次型 $f = \sum_{i, j = 1}^{n} a_{i j} x_{i} x_{j}$ ，总有正交变换 $x = P y$ ，使f化为标准形

$f = λ_{1} y_{1}^{2} + λ_{2} y_{2}^{2} + \dots + λ_{n} y_{n}^{2}$

其中， $λ_{1}, λ_{2}, \dots, λ_{n}$ 是f的矩阵 $A = (a_{i j})$ 的特征值。

定理2. 任给二次型 $f = \sum_{i, j = 1}^{n} a_{i j} x_{i} x_{j}$ ，总有可逆变换 $x = P y$ ，使f化为标准形

$f = λ_{1} y_{1}^{2} + λ_{2} y_{2}^{2} + \dots + λ_{n} y_{n}^{2}$

其中， $λ_{1}, λ_{2}, \dots, λ_{n}$ 不一定是f的矩阵 $A = (a_{i j})$ 的特征值。

在学习时，有些学生不清楚将一个二次型化为标准形的意义，不清楚利用正交变换和可逆变换的区别在哪里，可以结合具体的例子：化 $f = - 2 x_{1} x_{2} + 2 x_{1} x_{3} + 2 x_{2} x_{3}$ 为标准形。在给出具体的解题过程后，利用MATLAB编写程序，分别画出方程 $- 2 x y + 2 x z + 2 y z = 50$ 、正交变换下得到的方程 $- 2 x^{2} + y^{2} + z^{2} = 50$ 、可逆变换下得到的方程 $x^{2} + 2 y^{2} + z^{2} = 50$ 的图形，见图2。

通过借助MATLAB画图，学生可以直观感受到，通过正交变换，图形的形状没有发生变化，但是图形在坐标系中的位置发生了变化，它的方程可以用只含平方项的方程来表示，是学生熟悉的单叶双曲面的方程。当采用的是可逆变换时，该变换不会改变图形所属的类，但是会改变图形的形状，可以看到图形沿着y轴方向进行了压缩。在课堂演示时，还可以直接运行MATLAB软件，转动图形，引导学生从360度观察图形的形状，借助图形，增加可视性，易于学生理解，吸引学生注意，从直观上加深学生对这一部分内容的理解 [4]。

$- 2 x y + 2 x z + 2 y z = 50$ $- 2 x^{2} + y^{2} + z^{2} = 50$ $x^{2} + 2 y^{2} + z^{2} = 50$

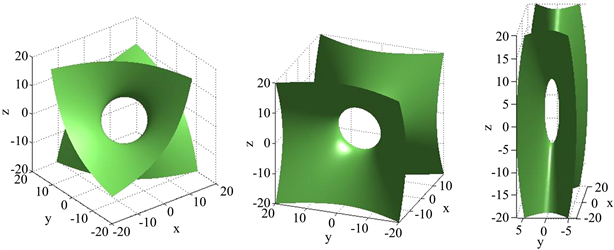
Figure 2. Geometry of quadratic form

图2. 二次型的几何图形

3.3. 借助MATLAB软件解决实际问题，增强了内容的实用性

很多实际应用问题的数学模型，都可以转化为线性问题来求解。然而，庞大的数据处理和复杂的计算步骤，使得这门课程的应用受到很大的限制。比如，下图给出了某城市单行街道的交通流量(每小时通过的车辆数)，见图3。

假定上述问题满足下列两个基本假设：

1) 全部流入网络的流量等于全部流出网络的流量；

2) 全部流入一个节点的流量等于流出此节点的流量。

Figure 3. Traffic flow diagram

图3. 交通流量图

根据上图及上述两个基本流量假设，可知所给问题满足如下线性方程组：

${\begin{cases} x_{2} - x_{3} + x_{4} = 300 \\ x_{4} + x_{5} = 500 \\ - x_{6} + x_{7} = 200 \\ x_{1} + x_{2} = 800 \\ x_{1} + x_{5} = 800 \\ x_{7} + x_{8} = 1000 \\ x_{9} = 400 \\ - x_{9} + x_{10} = 200 \\ x_{10} = 600 \\ x_{3} + x_{6} + x_{8} = 1000 \end{cases}$

解线性方程组的问题，都要用到初等变换的方法，将増广矩阵化为行最简形矩阵，这个过程只涉及到换行、倍乘和倍乘相加三种简单的运算，依次利用主对角线上的元素将所在列的其他元素化为0，即使对于一些变量较少的实际问题，虽然手算可以得到结果，但是既费时间又容易出错，枯燥的计算过程使学生产生厌倦情绪。

若将上述矩阵方程记为 $A X = b$ ，则问题就转化为求 $A X = b$ 的全部解。

下面利用MATLAB软件对上述方程进行求解，步骤如下

1) 输入系数矩阵A，并求A的秩，判断方程组解的情况

$\begin{matrix} A = [0, 1, - 1, 1, 0, 0, 0, 0, 0, 0; 0, 0, 0, 1, 1, 0, 0, 0, 0, 0; 0, 0, 0, 0, 0, - 1, 1, 0, 0, 0; \\ 1, 1, 0, 0, 0, 0, 0, 0, 0, 0; 1, 0, 0, 0, 1, 0, 0, 0, 0, 0; 0, 0, 0, 0, 0, 0, 1, 1, 0, 0; \\ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0; 0, 0, 0, 0, 0, 0, 0, 0, - 1, 1; 0, 0, 0, 0, 0, 0, 0, 0, 0, 1; \\ 0, 0, 1, 0, 0, 1, 0, 1, 0, 0]; \end{matrix}$

%线性方程组的系数矩阵

rank (A)；%求A的秩

2) 求增广矩阵的秩

$b = [300, 500, 200, 800, 800, 1000, 400, 200, 600, 1000];$

%常数b

rank ([A, b])%增广矩阵的秩。

由上可知系数矩阵的秩等于增广矩阵的秩，都为8，并且小于未知量的个数10，所以方程有无穷多个解。

3) 求非齐次线性方程组 $A X = b$ 的一个特解

取x₁和x₆为自由未知数，值分别为700和0，可得原方程组的一个特解为

$ξ^{*} = (700, 100, 200, 400, 100, 0, 200, 800, 400, 600)$ 。

4) 用null命令求出齐次线性方程组 $A X = 0$ 的基础解系。

x0 = null(A,’r’);

x0 =

−1 0

1 0

0 0

−1 0

1 0

0 −1

0 1

0 0

由此得到所求齐次线性方程组的基础解系为

$ξ_{1} = (\begin{matrix} - 1 \\ 1 \\ 0 \\ - 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}), ξ_{2} = (\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ - 1 \\ - 1 \\ 1 \\ 0 \\ 0 \end{matrix})$

综上所述，得到非齐次线性方程组 $A X = b$ 的通解为

$x = \bar{η} + ξ^{*} = c_{1} ξ_{1} + c_{2} ξ_{2} + ξ^{*} = c_{1} (\begin{matrix} - 1 \\ 1 \\ 0 \\ - 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}) + c_{2} (\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ - 1 \\ - 1 \\ 1 \\ 0 \\ 0 \end{matrix}) + (\begin{matrix} 700 \\ 100 \\ 200 \\ 400 \\ 100 \\ 0 \\ 200 \\ 800 \\ 400 \\ 600 \end{matrix}),$

c₁、c₂为任意常数。

在解的表示式中x的每一个分量即为交通网络中未知部分的具体流量，该问题有无穷多个解。Matlab的引入为用线性代数解决实际问题提供了有力的工具，学生在利用Matlab修改、分析数学模型的过程中，能加深对所学知识的理解，在探索的过程中体验到发现的愉悦。

4. 结束语

MATLAB自带的线性代数计算函数和命令，不仅使学生摆脱了线性代数问题求解中大量繁琐的计算过程，有更多的时间培养学生的抽象思维能力和逻辑推理能力，而且通过软件画图，在很大程度上减弱了线性代数的抽象性，使学生更容易直观理解各种概念并记忆深刻，增加了学生学习这门课程的兴趣，锻炼了学生的数学思维，为后续课程的学习及进一步研究打下了坚实的基础。如何将MATLAB更好的融入线性代数教学，还有很多值得进一步探讨的问题，也是我们以后教学过程中关注的重点问题。

参考文献

[1]	陈怀琛, 龚杰民. 线性代数实践及MATLAB入门[M]. 第2版. 北京: 电子工业出版社, 2009.
[2]	David C. Lay (美). 线性代数及其应用[Ｍ]. 北京: 机械工业出版社, 2006.
[3]	同济大学数学系. 工程数学——线性代数[M]. 第6版. 北京: 高等教育出版社, 2014.
[4]	王正盛. 中外线性代数教材的比较与探讨[J]. 大学数学, 2009, 25(1): 200-203.

为你推荐

友情链接