1. 背景介绍
法国数学家庞加莱发表的一系列论文将定性理论分析运用到微分方程的研究中,其结果在理论和实际应用中都发挥了重要的作用。关于定性理论的分析改变了人们以往的固有思维,为解决较难的数学问题提供了很好的思路。对于一些微分方程,求出特定解的意义不大,关键在于研究解的性质。毫无疑问,庞加莱的这一理论的提出实现了由定量到定性方向的转变。因此,可以说法国数学家庞加莱的成果为常微分方程定性理论的发展奠定了基础。它的基本思想是在不求出具体的微分方程解的条件下,研究该方程解的相关性质。
从上世纪开始,随着结构稳定性系统研究的逐渐快速发展,对分支理论的研究也受到越来越大的关注。分支理论悠久的历史背景和广泛的应用,推动了现代数学理论的发展。由微分方程定义的动力学系统分支种类有很多种。分支现象在自然界中也随处可见,因此在关于自然现象而建立的数学模型中可以找到许多的分支理论。由此可知,对分支理论的研究极具现实意义。重要的Hilbert第16问题是由希尔伯特提出的 [1],与Poincare分支有着密切的联系。许多数学家对这一问题进行了大量的研究。但是到目前为止,第16问题还没有得到彻底解决。该问题一方面是寻求“平面向量场的极限环个数的最小上界
并且找到极限环在什么位置上可能出现”。这是动力系统及其相关的常微分方程所研究的内容,其中
,
是关于x和y的次数为n的实数型多项式。
系统的最大极限环的个数
是一个与n相关的数,这是著名的Hilbert的猜想。到目前为止研究结果只发现,对于一个具体的系统,给出任意参数后,当
,
解析时,在
的情况下确实存在极限环的最大个数
,这一问题己经在1991年和1992年分别得到研究结果。但是对上述的所有n次系统的极限环的个数的有界性的问题的研究,在n = 2时的研究工作仍没有完全解决。由此,在1977年V. I. Arnold提出了新的解决这个问题的方法,那就是称作弱化的Hilbert-Arnold问题,也叫做弱化的第十六问题,即考虑如下的近哈密顿系统:
然而解决弱化的Hilbert-Arnold问题也是很困难的,并且可知研究弱化的第十六问题与估计Abel积分的零点个数密切相关。关于微小扰动下的哈密顿系统的极限环分支问题受到广泛关注。通过以上叙述可知一阶Melnikov函数对解决极限环的分支问题起着重要的作用。对于具有同宿环的系统来说研究极限环分支给出的多项式系统的展开式极为重要。借助于Melnikov函数展开式解决了很多系统的极限环分支问题,甚至说给出了哈密顿系统弱化的第十六问题的答案。研究Hilbert第16问题困难非常大,因而转向研究弱Hilbert第16问题。并且,估计Abel积分的零点个数是研究弱Hilbert第16问题的重要内容之一。将弱化的第十六问题转化为估计Abel积分的零点个数的问题,实现了问题的简化。因此,上述Abel积分的零点个数与极限环个数有着密切的关系。
本文对于具有普遍研究意义的n次扰动,研究Abel积分零点个数上界的这一内容仍存在许多尚未解决的问题。主要考虑含有扰动项的Liénard系统的阿贝尔积分,通过阿贝尔积分求系统的零点个数的最小上界。找到Liénard系统的阿贝尔积分零点个数上界,并证明阿贝尔积分的生成元能否构成Chebeyshev系统。利用I(h)的展开式和在Maensas和Villadelprat中开发的代数准则 [2],得出的结论是I(h)的零点个数的上限为3。
2. 预备知识
定理1 [3] 假设
是定义在开区间J上的解析函数,有以下定义:
1) 若任意的线性组合
在J上最多具有
个孤立零点,则
称为Chebyshev系统(简称T系统)。
2) 若任意线性组合
,对于
最多具有
个零点(考虑重数),则
称为扩充完全Chebyshev系统(简称ECT系统)。
3) 记
为如下行列式:
这称为有序函数列
的Wronski行列式。其中
是
一阶导数,
是
阶导数,
。
引理1 [3] 在
上,假设解析函数
满足
其中
,
,
是含于曲线族
的围绕原点的闭代数曲线。假设:
如果满足以下假设:
1) 当
时,
在
上存在,
2)
在
上有零点,用多重数计数,
3)
,
那么对于任意的非平凡线性组合
,在
最多有
上有零点,用多重数计数。同时,当
是
的Wronskian行列式时,
被称为具有精确度为k的在
上的T系统。
引理2 假定
是沿着
的一条闭轨线,
是满足
在
处解析的一元函数。当
时,以下等式成立,
.
引理3 当
时
则
是一个ECT系统,并且当且仅当
也是一个ECT系统。
引理4 当
时,函数元组
是一个ECT系统。
3. 证明过程
接下来,我们研究以下Liénard系统相对应的Abel积分
1977年,阿诺德(Arnold)提出弱化的希尔伯特(Hilbert)的第十六问题,目的是研究阿贝尔积分的零点数目
(1)
平面系统的形式为:
(2)
其中
,
和
是
函数,且
是一个非常小的参数。因此,(2)被称为带扰动项的哈密顿系统。
相应的无扰哈密顿系统:
(3)
近几十年来,许多研究人员专注于类型为(m, n)的Liénard系统
(4)
其中
和
是n和m阶的可微函数,特别重要的是(m, m − 1)的类型(见 [4] [5] [6] [7] )研究了(3, 2)型五个系统的阿贝尔积分,得到了不同的最小上界。对于(4, 3)型, [8] [9] 证明了阿贝尔积分零点的上界和下界分别为4和3。在本文中,研究了以下类型为(4, 3)的Liénard系统̇:
(5)
其中
,
是常系数。(5)为具有超椭圆哈密顿函数,对于系统(5)一些相关的定义和结果在 [10] [11] 中可以找到。
哈密顿量为:
(6)
哈密顿量对应的闭轨如图1所示。
为(6)的解析函数。考虑在平面上的如上形式的Hamilton函数:环绕中心O (0, 0)有一族顺时针方向的闭轨,
形成未扰系统的周期环域。设区间
是周期轨族在x轴上的投影。根据假设可知,
,
,因此,A(x)定义了满足
的一个对合
。
上的Melnikov函数为:
(7)
本文主要讨论当
,
和
,i = 0, 1, 2, 3的零点个数的上界,即目的是给出扰动系统在整个平面上零点个数的完整描述。
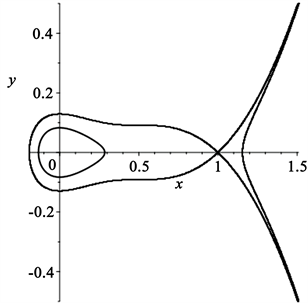
Figure 1. The portrait of system (5) when ε = 0.
图1. 系统(5)当ε = 0时的相图分支
根据引理1可知,引理一的第三个条件总是不满足,所以通常运用另一个引理。
本文根据引理2;
将I(h)乘以
可以得到:
(8)
设k = 3并且
运用引理2得到:
(9)
其中
将(9)带入到(8)中再乘以
,
(10)
应用引理2,取k = 5并且
,可以得到
(11)
其中
将(11)带入到(10)中再乘以
,可以得到:
(12)
再一次引用引理2,得
(13)
当
,其中
根据以上计算,很容易得到以下结果。
运用引理3取
(参见 [9] )
在
上定义了一个解析对合,
满足
和
。由
得
,其中
。
事实上,
是定义解析对合
的因式。
所以,当
(14)
假定
,换句话说,其中
,
(15)
根据斯图姆定理和相关分析技巧,运用Maple 19计算函数的4个Wronski行列式可得:
其中
,
是次数分别为22、44、64和90的多项式。
计算
和
关于z的结式得:
由Sturm定理得,在(0, 1)上
,即
和
没有满足条件的公共根,所以,
。因此,研究4个Wronski 行列式是否有零点转化为研究每个
(
) 是否有零点。因为z满足
,所以研究
和
是否有满足条件(15)的公共根即可。
1) 计算
和
关于z的结式得:
,其中
为关于x的70次多项式。由Sturm定理,当
时,
因此
和
没有满足条件(15)的公共根。得出结论:在(0, 1)上,
。
2) 类似地,检查
和
之间是否存在公共根,用
代替程序中的
,得到
,其中
为关于x的142次多项式。将Sturm定理应用于
,有两个点,用
和
表示,使得
,
。因此,将检查
和
在(0, 1)上是否有公共根,使用带有Maple 19的程序来查找所有可能的区间。
> with(RegularChains);
> with(ChainTools);
> with(SemiAlgebraicSetTools);
> sys := [w2(x,z), q(x,z)];
> R2 := PolynomialRing([x,z]);
> dec := Triangularize(sys, R2);
[regular chain]
> L := map(Equations, dec, R2);
得到正则链如下:
其中
,
,
和
是117、116和142次的多项式.前两条正则链之间没有公共根满足(15)。实根隔离第三条正则链得到
和
的所有公共根可能存在的8个区间对:
上述8个区间对是
和
在整个x-z平面上所有公共根存在的区间。这意味着没有一对满足条件(15)。可以说,
在
,因此,可以得到结论:
。
3) 接下来,要检查
和
之间是否存在公共根,我们用
代替程序中的
,我们得到:
其中
是关于x的216次多项式。将Sturm定理应用于
,有七个点,用
表示,
,
,
,
,
,
,
,使得
。
因此,我们将使用Maple 19程序查找所有可能的间隔,以检查
和
是否在(0, 1)上有任何公共根。
> with(RegularChains);
> with(ChainTools);
> with(SemiAlgebraicSetTools);
> sys := [w3(x,z), q(x,z)];
> R2 := PolyomialRing([x,z]);
> dec := Triangularize(sys, R2);
[regular chain]
> L := map(Equations, dec, R2);
得到正则链如下;
其中
,
,
,
分别是次数为174、174和216的多项式。显然,前两条正则链之间没有公共根满足(15)。实根隔离第三条正则链得到
和
的所有公共根可能存在的18个区间对(为节省版面,此处不列出)。我们发现所有区间对都不满足(15)的条件,这意味着
和
之间没有公共根,可以说
在
,因此,
4) 类似地,我们使用相同的程序来查找所有可能存在公共根的区间,这些区间可能存在
和
的公共根,然后得到以下正则链:
其中
,
和
和
分别是阶数为242、242和302的多项式。
将Sturm定理应用于
,有两个点,用
表示,
,
,
,
,
,
,使得
。很明显,前两条正则链之间没有公共的根(15)。实根隔离第三条正则链得到
和
的所有公共根存在的12个区间对。
发现所有区间对都不满足(15)的条件,可以说
在
,因此,
.
综上所述,根据定理1和引理4得到以下命题:
命题3.1
是
上的一个扩充完全Chebyshev系统,
也是。因此,
上的
最多有3个零点。
参考文献
NOTES
*通讯作者。