1. 引言
随着经济的发展和人民生活水平的提高,股票已经走入大众的视野。作为国家宏观经济的“晴雨表”,股票的市场价格直接关系到金融市场的稳定与发展。股票价格的复杂性、波动性以及高噪声、非线性性等特征使得准确预测股票价格具有一定的难度。
文献 [1] 基于传统的ARIMA模型来对股票的价格进行预测,预测结果在一定程度上可以代表股票的价格走势,但对于长期的趋势表现出了明显的局限性。随着人工智能及大数据的兴起,许多学者提出了使用机器学习算法来对股价进行预测 [2] [3],预测结果明显优于传统统计时间序列预测模型。文献 [4] 将随机森林应用到股票预测中,发现集成学习算法在股票预测中具有一定的作用。文献 [5] 使用SVM模型来对上证指数进行预测,相比于传统统计分析方法,SVM模型的预测值与实际值的误差率较低。为了解决机器学习模型的泛化能力不足的问题,采用深度学习来发现数据之间的潜在关系并进行建模,使模型在预测方面取得了较好的性能。文献 [6] 将GARCH模型与BP神经网络模型进行对比,发现无论是否考虑股票的波动性,GARCH模型的预测精度均优于BP模型。随后有学者将深度学习模型应用到股票预测中 [7],文献 [8] 提出了LSTM模型,有效的解决了循环神经网络在时间序列数据的预测中存在梯度消失及梯度爆炸的问题。文献 [9] [10] 基于LSTM神经网络来对沪深300指数的收盘价进行预测,试验结果表明LSTM模型对于股票价格的预测有显著的效果。但是LSTM模型只能通过历史数据来对未来某一时刻的值进行预测,学者们又提出了Bi-LSTM模型 [11],通过对历史数据与未来数据同时学习来预测未来某一时刻的值,使得模型的预测误差明显降低。
为了进一步提高股票价格预测的准确度,本文引入基于Adam优化算法的Bi-LSTM模型来对中国建设银行的股票价格进行预测,研究表明基于Adam优化算法的Bi-LSTM网络的精确度明显优于BP、LSTM、GRU等传统预测模型。
2. 模型和方法
2.1. Bi-LSTM的基本原理
LSTM (Long short-term memory)是循环网络RNN的一种,用来处理时间序列模型,LSTM模型采取了特殊的门结构,解决了RNN模型在训练过程中的梯度消失以及梯度爆炸等问题。LSTM模型的基本单元结构如图1所示,通过sigmoid函数对数据进行激活,充当门控信号;通过门控机制来控制信息的累积或遗忘。
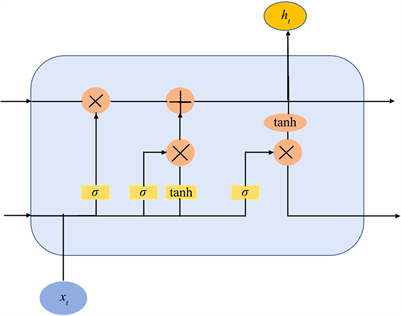
Figure 1. Basic unit structure of LSTM
图1. LSTM基本单元结构图
LSTM模型包含三个门结构:
1) 输入门:决定在t时刻是否会有信息输入到记忆细胞。
2) 遗忘门:决定将记忆细胞中的值遗忘掉还是保留下来。
3) 输出门:决定信息是否要从记忆细胞中输出。
LSTM的这种门控结构,能够更好适应于时间序列数据的处理,有效地解决长短时间序列变化上的问题。
LSTM的计算公式如下:
其中
和
为激活函数,计算公式分别为:
,
,
为t时刻的输入,
为t时刻的细胞状态,
为t时刻的临时细胞状态,
为隐藏层的状态,
、
、
为三个门控。
由于LSTM结构只能通过t时刻之前的信息来对 时刻的信息进行推断和预测,因此无法获得更多的相关信息来进行分析。为了提高预测的准确度,本文引入了Bi-LSTM模型来对股票价格进行预测。对t时刻前后的股票价格信息进行双向读取,使用前向及后向的历史数据来共同预测t时刻的股票收盘价。Bi-LSTM的基本结构如图2所示:
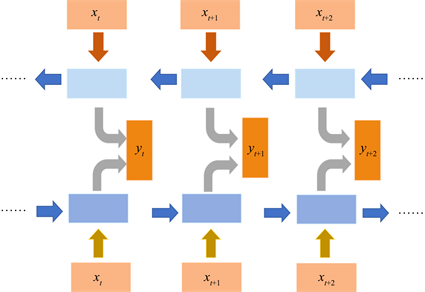
Figure 2. The basic structure of Bi-LSTM
图2. Bi-LSTM的基本结构
2.2. Adam优化算法
自适应矩估计(Adam)算法是将动量(momentum)和均方根传播(RMSprop)结合在一起的一种优化算法,通过对偏置进行矫正来使得参数更加平稳,使用Adam优化算法进行优化的步骤如表1所示:

Table 1. Adam optimization algorithm to optimize the steps
表1. Adam优化算法进行优化的步骤
其中
为一阶动量项,
为二阶动量项,均初始化为0,
,
分别为修正后的值,
为第t + 1次迭代模型的参数,
为学习率。在研究过程中,
,
,
的取值分别为0.9,0.999,
。
3. 性能评价指标
股票价格预测模型通常采用均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)、R2来对预测的精确度进行评价。MSE、RMSE、MAE的值越小,模型的预测精度越高。其中R2表示决定系数,范围在0~1之间,R2的值越接近于1表示真实值与预测值之间的相关度越高。这些误差评估方法的统计指标定义如下:
(5)
(6)
(7)
4. 算例分析
4.1. 基于Adam优化算法的Bi-LSTM风功率预测模型构建
Bi-LSTM是信息可以双向传播的LSTM结构,本文采用前9天股票的开盘价、最高价、最低价、收盘价、成交金额作为模型的输入,基于Bi-LSTM神经网络来对第10天的收盘价进行预测。
下面描述整个过程的详细步骤:
1) 将选取的数据分成训练集和测试集。在建立Bi-LSTM模型之前需要先对数据进行归一化处理,
归一化公式:
,通过数据归一化可以消除不同量级对预测结果产生的影响。
2) 将归一化后的数据处理为可以批量运算的矩阵来训练Bi-LSTM神经网络,确定模型参数,对测试集进行预测,将预测结果进行反归一化处理后与真实收盘价进行比较。
3) 采用多种误差评估方法来对模型的预测效果进行度量。并将Bi-LSTM模型的预测误差与BP、LSTM、GRU模型的预测误差进行比较。
4.2. 实验数据
本文研究所提出的模型及误差评定方法应用建行2011年1月4日~2021年5月25日共2522条数据。其中包括五个不同的变量,分别为开盘价、最高价、最低价、收盘价、总金额。首先对数据进行归一化处理,将前2018条数据作为训练集,将后504条数据作为测试集。
4.3. 数据描述
将建行数据的收盘价做折线图,如图3所示。
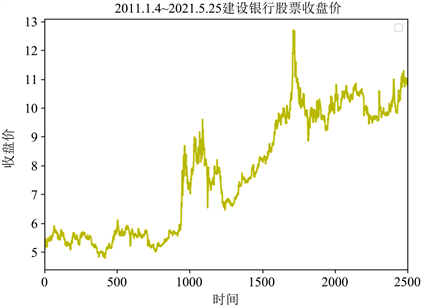
Figure 3. Line chart of Construction Bank stock
图3. 建设银行股票收盘价折线图
5. 参数设计
本节对本文提出的方法及BP、LSTM、GRU、Bi-LSTM四个不同模型进行了研究。所有的模型的实现都是基于python编程,其中BP、LSTM、GRU基于pytorch库实现。将Bi-LSTM模型的学习率设置为0.001,batch_size设置为64,本文通过前九天的股票价格来预测第十天的股票收盘价,将学习步长设置为9,股票数据有5个不同的变量,将Bi-LSTM模型的input_size设置为了5,hidden_size设置为512,output_size设置为1,经过多次重复实验,将Bi-LSTM模型的num_epochs设置为20。
6. 实验结果分析
对本文数据分别进行BP、LSTM、GRU、Bi-LSTM建模,图4为预测值与真实值的对比图。可以看出基于Bi-LSTM预测模型的预测值与真实值近似重合。
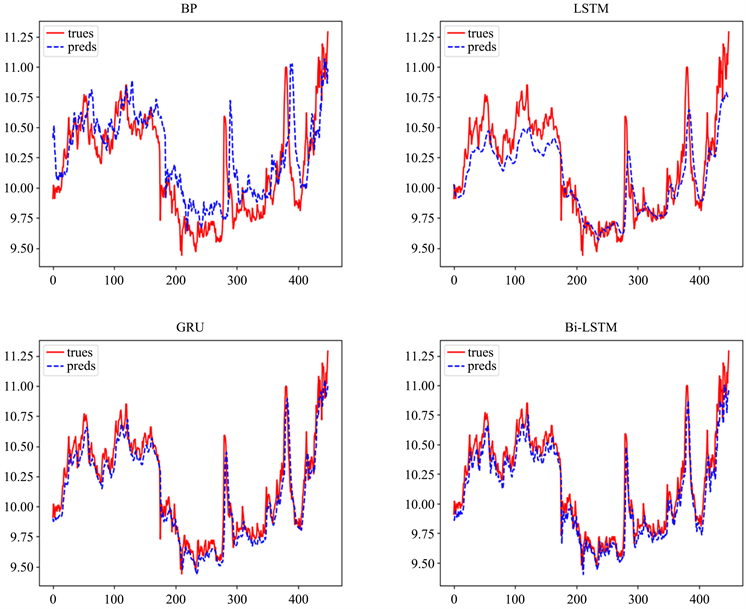
Figure 4. Comparison of predicted values and real values of different models
图4. 不同模型预测值与真实值对比图
将四个模型的预测值与真实值进行线性拟合做出散点图,如图5所示。从拟合散点图中可以看出,本文所提方法预测值与真实值非常接近。回归方程的各参数如表2所示,其中a表示回归系数,b表示截距,R2表示决定系数。
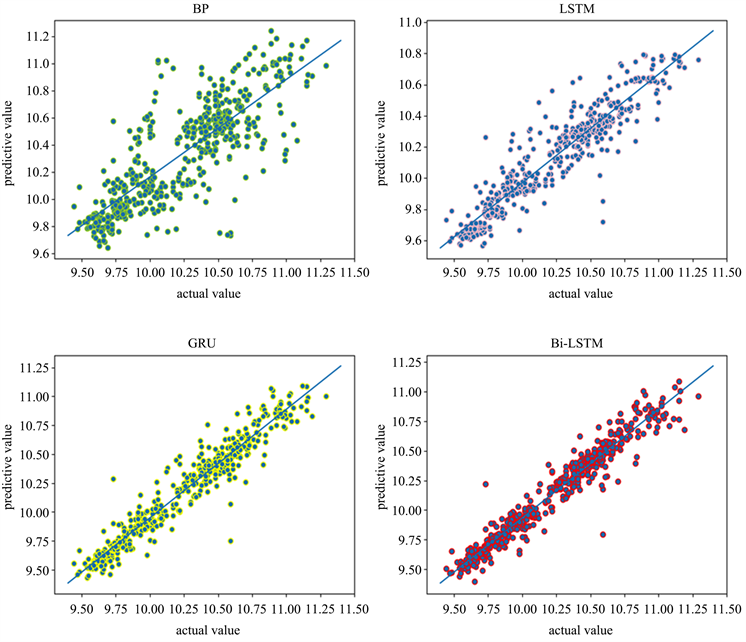
Figure 5. Fitting result graph of real value and predicted value
图5. 真实值与预测值拟合结果图

Table 2. Regression equation parameter table
表2. 回归方程参数表
为验证Bi-LSTM模型的准确度,本部分,将本文所提出的预测方法与BP、LSTM、GRU这三个模型进行比较,将预测结果进行对比分析。图6为本文所提模型与三个传统模型的预测结果,从图中,可以看出基于BP模型预测出来的结果与真实值的偏差最大,其余模型的预测值与真实值较为接近,其中Bi-LSTM模型预测的结果与真实值最为接近,本文所提出的Bi-LSTM预测模型能更好地对股票的收盘价进行预测。
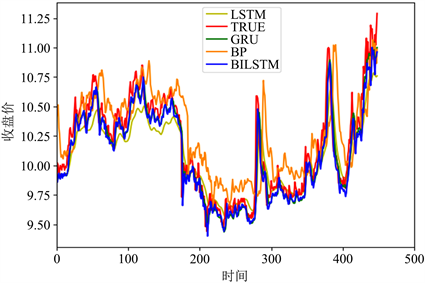
Figure 6. Comparison of predicted and true values of different models
图6. 不同模型的预测值与真实值对比图
为了进一步研究所提方法在不同时期的表现,对不同模型预测性能进行评估,分别使用不同的模型误差评估方法MSE、RMSE、MAE对四个模型的预测结果进行分析。表3和图7展示了误差结果,误差评估方法的值越小,模型的预测效果越好。由结果可以看出,本文所提模型Bi-LSTM的MSE、RMSE、MAE的值分别为0.0166、0.1282、0.969,均优于模型BP、LSTM、GRU的结果。说明本文所提模型的预测精度最为准确。
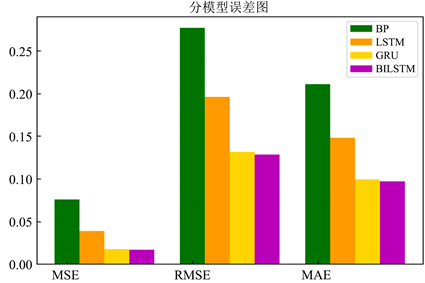
Figure 7. Error graph of different models
图7. 分模型误差图

Table 3. Model prediction error table
表3. 模型预测误差表
7. 结语
股票价格的预测在金融市场占据重要的地位,本文基于Adam优化算法的Bi-LSTM模型来对股票的收盘价进行预测。引入几种经典模型(BP、LSTM、GRU)来对本文预测模型结果进行分析,通过MSE、RMSE、MAE误差评估方法来对所有模型进行评估,误差评估方法MSE的结果表明,本文所提模型与BP、LSTM、GRU相比,精确度分别提高了77.95%、57.11%、2.36%。由于本文输入数据比较单一,可能会使得模型预测存在一定的局限性。下一步将通过论坛、贴吧等网站提取用户对股票的评论、新闻报道等相关信息,并对这些信息进行处理后加入到股票价格预测模型中,从多方面来对股票数据进行分析进而提高模型的预测精度。