1. 引言
随着在线自媒体和短视频的快速发展,对图像和其他多媒体数据的自动识别和分析的需求越来越大。然而,由于科技的飞速发展,很多领域却没有足量的有效标注数据,而通过人为进行数据的标注是十分昂贵并且耗费时间的,这导致了传统机器学习的局限性。因此,利用现有领域中充足的有标注数据来促进相关目标领域的模型学习的迁移学习方法是更经济、高效的方法。领域自适应是迁移学习在计算机视觉中对图片进行跨域识别的一种十分有效的方法 [1] [2]。
2. 相关工作
在这一节中,将介绍和本文相关的工作,潜在的低秩表征方法(Latent low-rank representation, LatLRR) [3],并且会详细介绍数据的交叉重构方法。
2.1. 潜在低秩表征
潜在低秩表征(Latent low-rank representation, LatLRR)是一种基于低秩表征的子空间学习方法,它能利用大量未观测样本来更好地表示原样本,它的原始目标函数如下:
(1)
其中,
代表能够观察到的数据,
代表着不能被直接观察到的数据,通过贝叶斯引理 [4],我们知道X可以被表示为
,则LatLRR的目标函数如下:
(2)
其中,
表示矩阵的核范数,它的值是矩阵所有奇异值之和,
表示矩阵的
范数,它的值为矩阵中的每个元素绝对值之和。Z是低秩约束的重构矩阵,C是投影矩阵,为了减少噪声的影响,LatLRR中引入了噪声矩阵E,最终的目标函数如下:
(3)
2.2. 交叉重构方法
在传统的领域自适应方法中,一般是把源域和目标域投影到一个子空间中,在这个子空间中,它们的分布差异较小 [5]。然而这些方法都没有很充分的利用原始数据,对数据潜在的关系挖掘不够充分。我们采取了一种新的数据重构方法来使得数据能够被有效利用。
和
分别表示原始的源域和目标域,本文构造两个新的数据域X和Y,我们分别从原始数据域
和
的每一类中随机抽取相同数目的样本数据,然后交叉混合作为新域的每一类数据。如果
,
(其中m 表示样本数据的维度,
和
分别表示源域和目标域中样本的数量)。我们让
和
分别表示从原始源域
和
的第i个类中抽取出的样本。则我们新构造的目标域可以被表示为:
和
。例如,在手写数字识别数据集USPS和MNIST中包含10个类,我们实验的时候从原始源域和目标域的每个类中抽取5个样本构成我们新域中的一个包含10个样本特征的类。L表示我们所构建的两个域的标签(他们的标签是一样的)。
通过数据的交叉重构,原始数据的每一个类都得到了很好地对齐,再通过LatLRR方法,我们能够把源域和目标域的主要信息提取出来,使它们相同类可以做到相互表征,这样就很好的把源域和目标域数据中相同标签类数据做到了很好的局部对齐。如此,得到新构成数据域的相互表示
。只要再把分类器的学习统一到框架中,就得到了我们的交叉重构领域自适应方法。
3. 交叉重构的领域自适应方法
这一章节,将详细介绍交叉重构的领域自适应(Cross Reconstruction-based Domain Adaptation, CRDA)方法。第一小节介绍它的目标函数。第二小节介绍它的优化方法和主要步骤。
3.1. CRDA的目标函数
由于低秩矩阵C能够很好的提取出数据的显著特征,考虑用C来作为的跨域识别分类器。于是,得到CRDA的目标函数如下:
(4)
其中,
表示矩阵的Frobenius范数,值为矩阵中每个元素的平方和再开平方的值。
表示矩阵的2,1范数,它的值是矩阵每一行的
范数之和 [6]。
是惩罚系数,用于调整每一项的权重。
3.2. CRDA的优化计算方法
基于凸优化理论,可知本文的目标函数整体是非凸的,但是每个变量
的优化都是凸优化问题 [7]。因此本文使用迭代更新方式来优化目标函数(4)。为方便优化,我们引入辅助变量
替代
。将(4)中的目标函数重写为以下形式:
(5)
式子(5)的增广拉格朗日函数为:
(6)
其中,
是拉格朗日乘子,
是惩罚系数。变量通过交替方向乘子法(Alternating Direction Method of Multipliers, ADMM) [8] 更新,更新一个系数时,会保证其他的系数固定不变。迭代优化步骤如下:
步骤1 (更新A):固定H,Z,C,E,并求解以下式子:
(7)
令
,通过令偏导
,可以得到A的解如下:
步骤2 (更新H):固定A,Z,C,E,可以通过求解以下式子:
(8)
可以得到H的解如下:
步骤3 (更新Z):固定A,H,C,E,并求解以下式子:
(9)
令
,通过求
,得到Z的解为:
步骤4 (更新C):固定A,H,Z,E,并求解以下式子:
(10)
令
,通过求
得到C的解为:
(I为单位矩阵)
步骤5 (更新E),固定A,H,Z,C,并求解以下式子:
(11)
对于(11),可以根据以下引理来求解 [9]:
引理1:对于问题:
其中Q是一个已知矩阵,如果该问题的最优解是
,那么
的第i列的值如下:
用
替换其中的
,用
替换其中的Q,就能够得到E的解
算法1总结了CRDA的优化框架如下:
4. 实验
为了验证交叉重构领域适应方法(CRDA)的有效性,这一节将让CRDA在COIL20, MNIST & USPS, MSRC & VOC2007, Office & Caltech 和Office-Home这5个基准数据集上分别进行实验。从这些数据集的源域和目标域的每一类中随机抽取5个样本来构造新的数据域,剩下的数据作为测试样本使用。通过CRDA得到分类矩阵A,使用AX来作为最后的分类标签。如果第i个测试样本的特征向量为
,通过计算得到它的标签向量
,则标签向量
中最大值所处位置为该样本所属标签类。例如,我们得到了第i个测试样本的标签向量
,并且
,其中
,则我们把这个样本划分到第k类数据当中。实验在Matlab2019b, Intel(R) Core(TM) i7-6700 CPU @3.40GHz环境下进行,为了保证实验结果的有效性,CRDA算法的最终的识别效率为20次实验的平均值。
4.1. 数据集介绍
COIL 20数据集:该数据集包含20个不同对象以360度旋转成像。每旋转5度收集一张物体的图像,即每个物体有72幅图像,均为不同角度,共1440张图像。所有的图片裁剪并转换为32 × 32像素的灰度图像。
MSRC & VOC2007数据集:MSRC包含了18个层次的4323幅图像,而VOC 2007包含了20个概念的5011幅图像,它们分别共享了飞机、羊、汽车、牛、鸟、自行车6个语义类,并且将所有图像调整为256像素。
MNIST & USPS数据集:该数据集中有7291幅训练图像和2007幅测试图像;MNIST数据集中有60,000幅训练图像和10,000幅测试图像,这两个数据集共有10个语义类,每个语义类对应数字0~9,所有的图片都被转换为16 × 16像素的灰度图像。
Office & Caltech256数据集:Office数据集是视觉对象识别的基准数据,包括来自三个不同领域的常见对象类别,即A(Amazon)、W(Webcam)和D(DSLR),每个领域共有31个对象类别。例如笔记本电脑、键盘、显示器、自行车等,一共含有4652张图片。在Amazon域中,每个类别平均有90张图片,而在DSLR或Webcam域中,每个类别平均有30张图片。Caltech-256数据集是用于目标识别的标准数据集,有30,607幅图像和256个类别。
Office-Home数据集:该数据集由来自4个不同领域的图像组成:艺术图像、剪辑艺术、产品图像、现实世界图像,对于每个领域,数据集包含65个对象类别的图像,通常在办公室和家庭中发现。实验中的数据特征是由预先训练好的ResNet50模型提取得到的。
4.2. 超参数设置
如式(5)所示,CRDA中包3个超参数,他们分别是
,它们的取值范围都设定为
,超参数的最后取值通过网格搜索策略确定。对于数据集COIL 20,最终参数选择为
;对于数据集MSRC & VOC2007,最终参数选择为
;对于数据集MNIST & USPS,最终参数选择为
;对于数据集Office & Caltech,最终参数的选择为
;对于Office-Home数据集,最终参数选择为
。
4.3. 实验结果和分析
为了验证CRDA算法的有效性,我们选取了几个迁移学习和领域适应的基线方法做对比,它们分别是Geodesicflow Kernel (GFK) [10], Low-rank Transfer Subspace Learning (LTSL) [11], Fisher Discrimination Dictionary Learning (FDDL) [12], Joint Geometrical and Statistical Alignment (JGSA) [13], Weakly-Supervised Cross-Domain Dictionary Learning for Visual Recognition (WSCDDL) [14], Visual Domain Adaptation with Manifold Embedded Distribution Alignment (MEDA) [15]。
4.3.1. 实验结果
表1展示了CRDA与对比算法在COIL20、MSRC & VOC2007、MNIST & USPS这三个数据集上的识别准确率。表2展示了CRDA与对比算法在Office + Caltech256数据集上的识别准确率。表3展示了CRDA与对比算法在Office-Home数据集上的识别准确率。

Table 1. Experimental results on three different datasets
表1. 在三个不同数据集上的实验结果

Table 2. Experimental results on the Office + Caltech dataset
表2. 在Office + Caltech数据集上的实验结果

Table 3. Experimental results on the Office-Home dataset
表3. 在Office-Home数据集上的实验结果
4.3.2. 实验结果分析
对于上述实验结果,我们进行如下分析:
1). 该方法在大多数数据集上的性能都优于与之比较的方法。这表明,使用改进的类PCA正则化项,CRDA能够很好地保存数据信息。此外,通过对重构矩阵施加低秩约束,可以将来自不同领域但共享同一标签的数据很好的对齐。这就保证了新的特征表示的识别性,因此我们的方法可以显著提高识别准确率。
2). 在高维数据集 Office-home上的实验结果表明,CRDA在大多数高维数据集上表现良好。结果表明,我们的方法能够很好的处理高维度数据。
3). 在半监督领域适应中,人工添加伪标签的对抗式方法是很常见的。在本文中,我们使用原始数据重构代替伪标签来提高分类精度。通过实验,我们发现CRDA的性能比MEDA更好,证明了我们方法的有效性。
4.3.3. 模型收敛性分析
ADMM在只有两个或更少块时的收敛性已经被证明。算法1有7个分块,没有严格的理论收敛性支持。然而,一些理论可以扩展ADMM的收敛性的范围。例如,Jia等人在单个函数是强凸函数和线性函数复合 [16] 的前提下证明了具有两个块的可分离凸规划的经典ADMM可以推广到三个或三个以上的块。Hong等人证明了在增广拉格朗日函数 [17] 中惩罚参数足够大的情况下,经典ADMM收敛于平稳解集。Luo和Hong指出,当线性约束的非光滑凸可分离函数的和最小时,ADMM与n(n > 2)变量块也可以收敛 [18]。从图1的实验结果中可以证明,CRDA算法是有效收敛的。
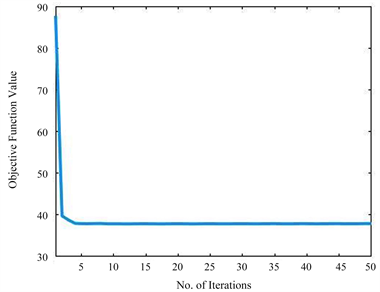 (a). COIL20 (COIL2 -> COIL1)
(a). COIL20 (COIL2 -> COIL1)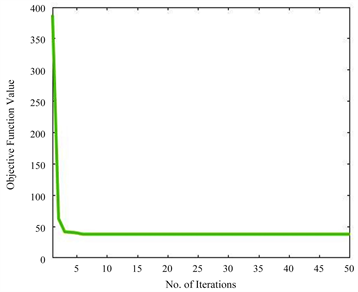 (b). Office-Home (Pr -> Ar)
(b). Office-Home (Pr -> Ar)
Figure 1. Curve: Model convergence analysis
图1. 模型收敛性分析
4.3.4. 参数敏感性分析
从图2中我们可以发现,在CRDA中,随着
的变化,识别准确率的变化不大,这是因为
控制的是低秩矩阵的权重,而低秩矩阵本身就很小,
使得它更小,所以对识别准确率的影响不大。随着
的增大,识别准确率会有一个先减小再增大再减小的趋势,这是因为
控制的是噪声矩阵所占的比重,随着它的变化,分类器的比重会相应的变化,所以对识别准确率的影响是波动的。
控制的是分类器权重,从图中我们可以知道,对于不同的数据集,随着
的增长,准确率的变化是不同的,说明分类器矩阵和数据集是十分相关的。
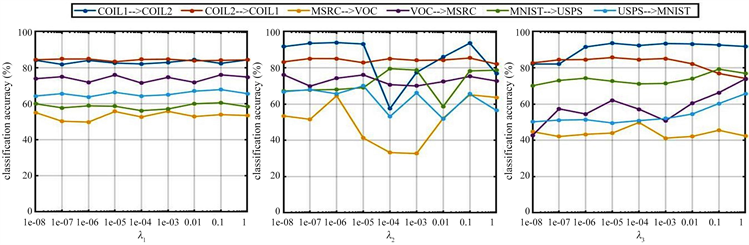
Figure 2. Curve: The effect of
on the classification accuracy
图2. 超参数
对识别准确率的影响
5. 结论
本文提出了一种基于交叉重构的领域自适应算法用于跨域识别。该算法通过将源域和目标域数据进行交叉重构来使原始源域和目标域做到相互表示,同时对重构矩阵施加低秩约束来对齐同类数据,从而挖掘同类数据间的相似性,以最大程度保留数据主要信息。最后对分类矩阵施加稀疏约束,来去除数据冗余信息,达到提高模型性能的目的。在5个常用的数据集COIL20,MNIST & USPS, MSRC&VOC2007, Office & Caltech, Office-Home上验证模型的有效性。实验结果显示,与其他相关的传统领域自适应方法相比,CRDA算法能更好地保留投影数据信息,取得更好的跨域识别效果。