1. 引言
西南地区由于近期构造运动强烈,河流急剧下切,形成了高山峡谷地貌。沟谷两岸多陡坡,岩石风化强烈,岩体破碎,崩塌、滑坡、泥石流等物理地质现象发育;沟谷中细粒物质淤积,地下水丰富,多发育淤泥、泥炭等软土;同时西南地区地震活动强烈,活动断裂紧邻很多已建或拟建的公路、铁路、机场、水电站的大型工程建筑,甚至部分断裂横穿整个工程场地,由此带来了一系列的工程地质问题 [1]。5.12汶川地震、4.14玉树地震、4.20芦山地震等引发了大量的地质灾害,许多道路、房屋建筑、机场受到不同程度的损坏,这反映出工程地震安全性评价的不足 [2] [3] [4] [5] [6]。以往边坡地震动响应特征及稳定性研究,大都集中于对自然斜坡的研究,而对填方边坡尤其是西部高原地区,巨高填方边坡的地震动响应特征研究还较少,因此开展西部高原地区高填方边坡的地震动相应分析、研究,对于类似地区的工程建设、科研、防灾减灾等具有重要意义。
以往国内外学者多采用拟静力法进行地震动响应分析,拟静力法虽然简单,但是却有许多不足之处,如假定边坡为刚体,地震加速度恒定不变而在地震中,惯性力不是恒定不变的,也不是单向的,而是在量级和方向上都有快速的波动 [7] [8]。边坡在静力作用下的稳定性与动力作用下的稳定性有一定的相似性,但是也存在众多差异,边坡的静力稳定性分析是边坡动力稳定性分析的基础,也是动力问题的特例,静力问题实质上可以视为“拟动力”。
随着计算机技术的迅速发展,数值分析法得到了广泛的运用,其优势在于能综合考虑地质结构、岩土条件、水力条件、地震动条件等因素,并进行地震作用下地质体的变形、稳定分析 [9] [10] [11] [12]。
2. 高填方边坡的主要震害
高填方在地震影响下的主要震害有:填方体的竖向不均匀沉陷;填方边坡的开裂、错落、垮塌、滑坡破坏;填方体顶平面的隆起、挤压、拉裂;支挡结构和防护工程的破坏等。
2.1. 填方体竖向不均匀沉陷
填方体竖向不均匀沉陷是填方结构的主要震害模式,按产生原因大致可分为两种情况:地面沉陷引起填方体沉陷和填方体填料振密及侧向变形引起的道面沉陷。
地面沉陷引起填方体沉陷是因为,填方原地基沉陷会引起填方体的沉陷,地震诱发地面沉陷的主要因素有砂土液化、软土陷害等。填料振密和侧向变形引起的填方体沉陷是由于,地震作用下,填方体填料会产生不同程度的振密。填方体有临空面,在地震水平力作用下,很容易产生侧向变形,从而引起填方体下沉。地震中,填方体填料振密与侧向变形往往同时产生,二者共同导致填方体下沉。
2.2. 填方边坡开裂、错落、垮塌、滑移
地震作用下边坡产生不规则的张拉破裂带,往往在边坡后缘出现宽大裂隙,而在坡脚部位推挤隆起,形成局部错动和滑移,严重时会出现填方体整体垮塌。
对于半挖半填边坡,由于填筑体与原地基力学性质不同,地震时填筑体易沿填挖交界面或岩土分界面滑移、错动形成贯穿裂缝,导致填方边坡整体破坏。同时地震使填筑体内部裂隙得到发展,填土变得松散,为降雨入渗、地下水潜蚀作用创造了条件,加速滑坡的形成。
2.3. 填方顶面的隆起、拉裂
填方边坡顶面的隆起,主要是由于持续的地震作用导致填方体顶面相互挤压,产生鼓包和陷坑,形成波浪状、台阶状错动破坏,在隆起部位产生众多横向张裂缝。
2.4. 支挡结构和防护工程的震害
填方边坡支挡和防护结构震害主要包括挡墙、抗滑桩、桩板墙、格构的变形、断裂、滑移等。
3. 高填方边坡地震动响应特征分析
3.1. 工程概况
甘孜机场跑道长4000 m,宽45 m,两侧土面区宽约91 m,西北端标高4062.7 m,东南端标高4055.4 m,挖填土石方总量约5850万方,最大挖方高度约60 m,最大填方高度约109 m (九寨黄龙机场最大填方高度为104 m,建成后填方高度在民航界中属世界第一),属于典型的高高原巨高填方机场,见图1。机场抗震设防烈度8度,基本地震加速度0.2 g。

Figure 1. Engineering features of ganzi airport in construction
图1. 建设阶段的甘孜机场工程特征
1) 区域地质情况

Figure 2. Geological Structure Outline of Ganzi Airport
图2. 甘孜机场区域地质构造纲要图
在建甘孜机场位于四川省西部,大地构造单元上地处松潘–甘孜造山带,地处鲜水河断裂中段的西侧,甘孜–理塘断裂带北侧,其主体构造呈NW向。甘孜–玉树断裂对场区的影响较大,存在发生7级以上地震的可能 [13]。研究区主要受NW向多条断裂共同控制,地质构造作用十分强烈,场区构造,如图2。
2) 工程区地形地貌
机场场址位于近东西向山梁之上,地势中间高,两侧低。山体呈波状起伏,顶面高程3966~4142 m,平均高程4090 m左右;沟谷切割强度小,呈宽缓的“U”型槽谷,流向多为NNE和SSW向。工程区属于构造–剥蚀地貌,微地貌分区又可以分为:丘状岭脊区,坳沟区,丘状台地区,丘状沟槽区,斜坡区和沼泽相平原区 [14],如图3。
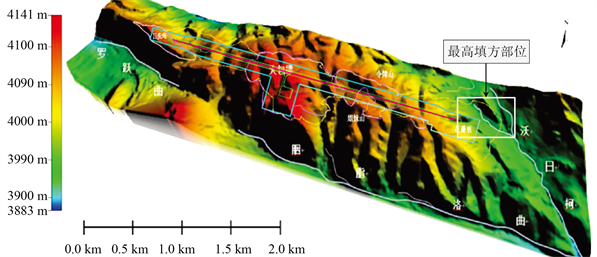
Figure 3. Terrain and geomorphic features of the engineering area
图3. 工程区地形地貌特征
3) 工程区岩土特性
研究区地层岩性比较复杂,第四系主要有植物土(Q4pd)、泥炭(Q4h)、残坡积粉质粘土(Q4el+dl)、坡洪积粉质粘土(Q4dl+pl)及碎石(Q4dl+pl),基岩主要有灰岩(Tt2)、变质砂岩(PTkr)、角砾岩(PTkr)。
3.2. 边坡动力响应时程分析
1) 计算模型的建立
选取机场东端沃日柯地区N.01高填方边坡进行研究,该边坡坡高约140 m,垂直填方高度约102 m,边坡剖面在原地面及填筑完成后展布特征如图4、图5,边坡计算模型岩土分层特征如图6所示。

Figure 4. Overall distribution characteristics before filling in the study area
图4. 研究区填方前总体展布特征
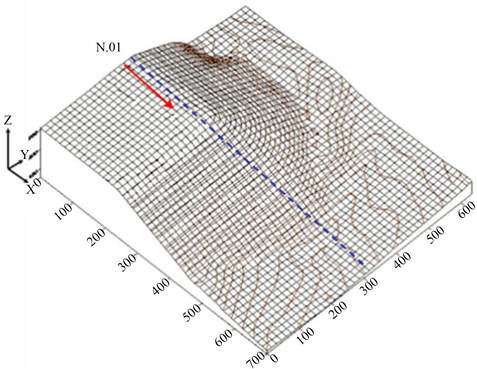
Figure 5. Overall distribution characteristics after filling in the study area
图5. 研究区填方后总体展布特征
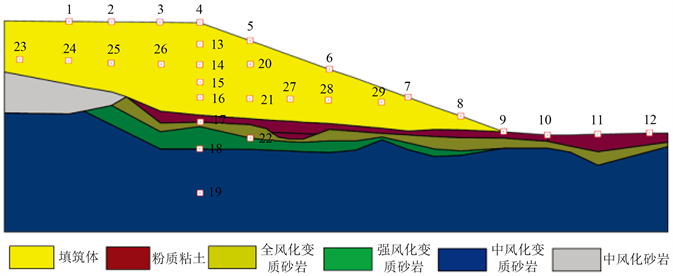
Figure 6. Computational model of rock and soil layering
图6. 计算模型岩土分层特征
模型计算参数依据机场详细勘察、高填方专项勘察原位试验及室内试验成果、试验段现场检测成果,并结合工程经验综合取值获得,各岩土层物理力学参数,如表1。

Table 1. Physical and mechanical parameters of calculation model
表1. 计算模型岩土层物理力学参数表
2) 地震波的合成
地震动具有不可精确预测性和不可重复性的特征,由于真实的地震波难以在获得,目前普遍采用人工合成地震波进行地震动分析。地震动时程的合成采用《工程场地地震安全性评价》(GB 17741-2005) [15] 技术标准或《地震安全性评价技术教程》 [16] 推荐的方法,本文采用的地震波数据引自地震安全性评价报告相关成果,主要采用国家地震局推荐的地震危险性分析程序包,计算得到了工程场地在不同超越概率水平下的地震烈度值、基岩水平峰值加速度及基岩水平加速度反应谱。
人工地震波合成的基本思路是用一个三角级数构造平稳高斯过程,然后乘以确定性的包线,得到非平稳过程,其形式如式(1)。
(式1)
式中,
为相角,通常认为是在(0, 2π)区间内均匀随机分布;
与
分别为第k个频率;
为强度包线。在拟合目标反应谱时,首先选择一个初始时程
,计算这一时程的反应谱,根据计算结果与目标反应谱的差异来调整幅值谱
,从而生成新的时间过程;重复上述过程直到时程的反应谱与目标普满足误差要求为止。
本次选用地震安全性评价人工合成的50年超越概率63% (等效地震烈度6.5度)、10% (等效地震烈度8度)的地震加速度时程。截取前28 s时程数据,单位时间步长0.02 s,总共1400个数据点。P50 = 10%水平地震加速度时程曲线,如图7。
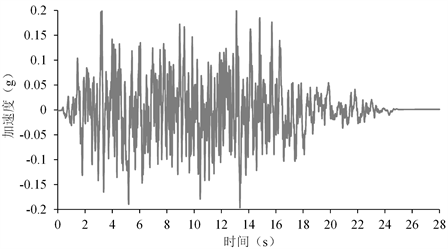
Figure 7. 10% acceleration time history curve
图7. 超越概率10%加速度时程曲线
3) 边界条件设定
① 底部边界假定水平和竖直方向均为固定;② 侧向边界由于斜坡体存在自重应力,且自重应力对填方体的固结沉降和斜坡稳定性影响非常大,地震作用下基岩及填方体向后缘无限延伸,水平位移较小,因此假定水平向固定,竖直向自由;③ 顶部边界水平和竖直方向均为自由;④ 阻尼比系数λ = 0.05;⑤ 放坡比1:2.5。
4) 时程计算方案
按照如图8的技术路线进行各条件下边坡地震动响应和变形特征分析。

Figure 8. Ground motion analysis technology route
图8. 地震动分析技术路线图
5) 结果分析
① 地震烈度对边坡变形的影响
地震烈度6.5度,清表 + 清除泥炭层不做其他地基处理的条件下。边坡X向最大相对位移0.097 m,Y向最大相对位移0.054 m,边坡永久变形量0.098 m,变形区域集中于边坡顶部,如图9。
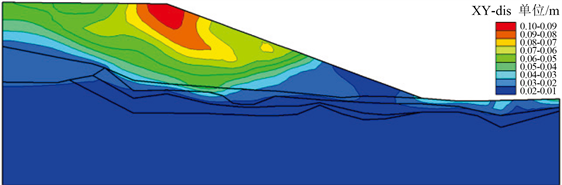
Figure 9. Characteristics of permanent deformation of slope with earthquake intensity of 6.5 degrees
图9. 地震烈度6.5度边坡永久变形特征
地震烈度8.0度,边坡X向最大相对位移0.282 m,Y向最大相对位移0.164 m,边坡永久变形量0.305 m,变形区域位于边坡上部,且变形区域表现出向坡顶后缘和边坡中下部扩展的趋势,塑性变形区与6.5度相比明显增大,如图10。

Figure 10. Characteristics of permanent deformation of slopes with earthquake intensity of 8.0 degrees
图10. 地震烈度8.0度边坡永久变形特征
监测数据显示,烈度8.5度与6.5度相比,边坡永久变形量增大了约5倍,可见边坡动力变形与地震烈度呈正相关关系。位移数据反映出X向位移大于Y向位移,说明了水平向地震作用更易激发边坡的变形,且得出边坡坡面位置,尤其是坡顶部位对地震的反应较为敏感,是主要的变形破坏区。
② 边坡不同坡比动力响应分析
合理的放坡坡比对确保边坡稳定十分重要,同时还影响到边坡的抗震性能。研究中采取1:2.5、1:3.0两种放坡进行对比分析,主要采取以下几种方案:
A——坡比1:2.5放坡与1:3.0不进行地基处理条件下动力响应对比分析;
B——坡比1:2.5条件下地基处理前后边坡动力响应分析;
C——坡比1:2.5放坡与1:3.0地基处理后动力响应对比分析。
(A) 坡比1:2.5与1:3.0不进行地基处理条件下动力响应对比分析
结果表明,1:3.0放坡与1:2.5放坡相比,边坡整体变形量有所减小,特别是坡顶部位的塑性变形区变化较明显,如图11,坡脚X向相对位移也有部分减小。
(B) 坡比1:2.5地基处理前后边坡动力响应分析
对填方边坡底部粉质粘土进行换填,换填深度一般1~8 m,土层厚度 < 5 m部位进行全部换填,土层厚度 > 10 m部位进行部分换填,并进行强夯处理。处理后与处理前相比,坡顶永久变形量减小了5.25%,中部减小了26.6%,坡脚减小了1.1%。可见,地基处理对边坡中部变形影响较明显,主要原因在于,边坡中部填筑体底部原地基存在深厚粉质粘土层,地基处理后承载力得到大幅提高,不均匀变形将减小,如图12。因此,地基处理对减小边坡地震变形是有效的,可以有效提高地基承载力,降低地震引发填方边坡产生过大沉降、不均匀沉降、坡面变形的风险。
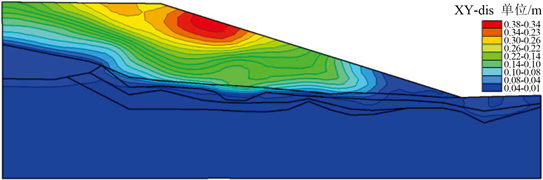
Figure 11. Intensity 8.0 Permanent deformation of slope (1:3.0 Gradation)
图11. 烈度8.0边坡永久变形特征(坡比1:3.0)
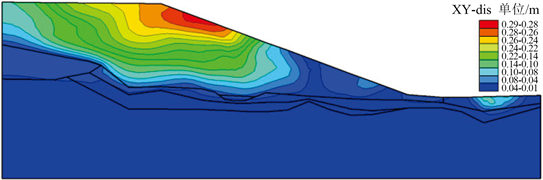
Figure 12. Characteristics of permanent deformation of slope after foundation treatment (1:3.0 Gradation)
图12. 1:2.5放坡地基处理后边坡永久变形特征(坡比1:3.0)
换填前后,坡顶4#、中部6#、坡脚8#监测点X、Y向相对位移时程曲线,如图13~16。
换填前后,坡顶及中部4#、6#监测点峰值加速度时程曲线,如图17~20。
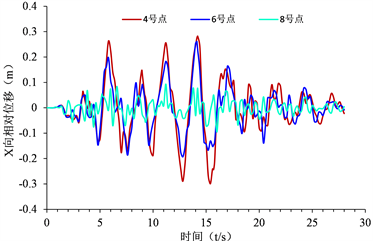
Figure 13. X-direction relative displacement of slope monitoring point before replacement
图13. 换填前坡面监测点X向相对位移
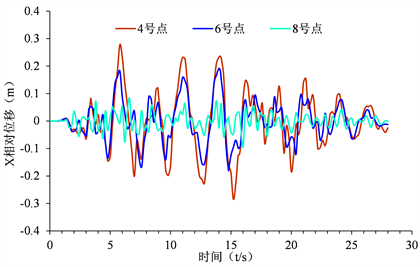
Figure 14. Relative displacement in X direction of slope monitoring point after replacement
图14. 换填后坡面监测点X向相对位移
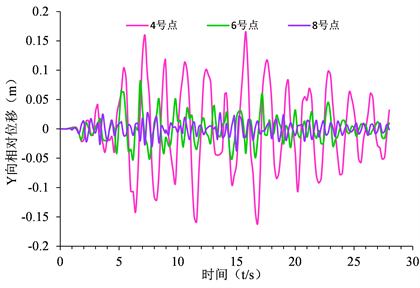
Figure 15. Relative displacement in Y direction of monitoring point of slope surface before replacement
图15. 换填前坡面监测点Y向相对位移
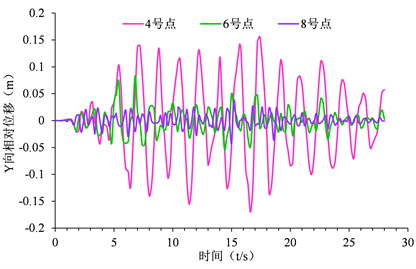
Figure 16. Relative displacement in Y direction of slope monitoring point after replacement
图16. 换填后坡面监测点Y向相对位移
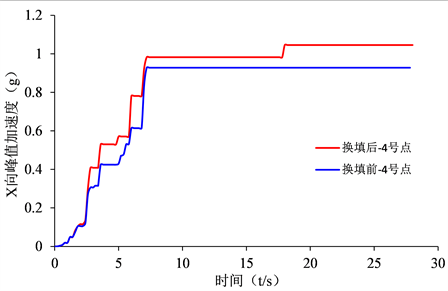
Figure 17. 4# point X-direction peak acceleration
图17. 4#点X向峰值加速度
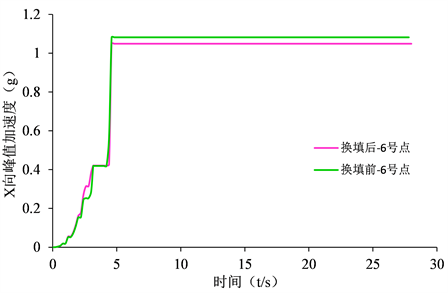
Figure 18. 4# point Y-direction peak acceleration
图18. 4#点Y向峰值加速度
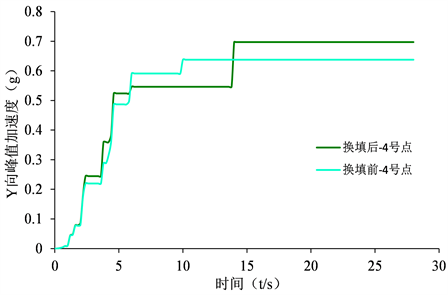
Figure 19. 6# point X-direction peak acceleration
图19. 6#点X向峰值加速度

Figure 20. 6# point Y-direction peak acceleration
图20. 6#点Y向峰值加速度
换填后4号点、8号点的峰值加速度大于了换填前的峰值加速度,只有6号点换填后的峰值加速度小于换填前的峰值加速度,这说明填方地基软弱基层具有一定的隔震作用,换填后填方体厚度增大,反而对地震波有一定程度的放大作用,但放大作用有限对边坡影响较小。
(C) 坡比1:2.5与1:3.0地基处理后边坡动力响应分析
1:2.5放坡地基处理后坡顶4号监测点X向最大相对位移0.278 m,Y向最大相对位移0.156 m,边坡永久变形量0.289 m;1:3.0放坡地基处理后X向最大相对位移0.266 m,Y向最大相对位移0.178 m,边坡永久变形量0.292 m。初步得出,增大放坡坡比后结合进行地基处理对减小边坡X向永久位移有效,对减小Y向永久作用不明显。6号、8号监测点显示增大坡比并进行地基处理对减小边坡Y向永久位移具有一定效果,但对减小X向永久位移效果不明显。
③ 坡脚反压对边坡动力响应的影响
坡脚设置反压平台,反压平台高度H = 30 m,长度D = 115 m,放坡坡比1:3.0~1:3.5。
计算获得无反压与反压情况下坡面顶部、中部、坡脚部位监测点位移特征,如表2。
结果显示,设置反压平台对减小边坡中部及上部动力位移效果较好,如图21。坡脚反压可有效改善边坡的应力分布,特别对改善坡脚部位的应力分布效果最明显,减小坡脚的应力集中程度,增加边坡的抗滑力,提高边坡的稳定性。
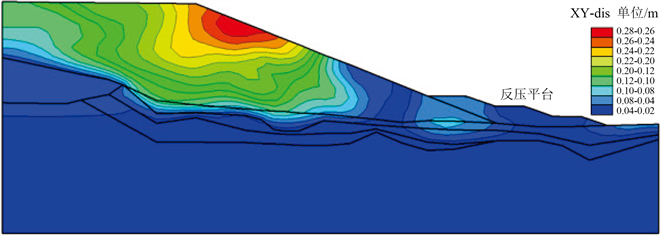
Figure 21. 1:3.0 Characteristics of permanent deformation of slope foot anti-pressure slope
图21. 坡脚反压边坡永久变形特征

Table 2. Changes in peak acceleration at slope monitoring points before and after backpressure
表2. 反压前后坡面监测点峰值加速度变化
由上表可知,反压情况下坡面各点的地震峰值加速度普遍小于无反压情况下的峰值加速度,特别是坡顶和坡脚部位变化特别明显。坡顶反压后X向峰值加速度平均减小了7.5%,坡脚部位平均减小了28.35%。可见采取反压措施可有效的降低边坡的地震加速度,从而降低边坡地震动响应程度。
④ 边坡的位移及加速度高程放大效应特征
边坡内部相同X坐标下,不同高程位置地震动响应特征,选取坡顶位置对应监测点4、13、14、15、16、17#监测点进行定量分析,监测点计算结果,如表3。

Table 3. Statistics of ground motion response data at vertical monitoring points on slope tops
表3. 坡顶垂向监测点地震动响应数据统计
随着竖直向填方高度的增加,边坡整体X、Y向位移无明显变化;X、Y向相对位移与垂向填方高度呈指数正相关关系,如图22、图23。X向加速度与垂向填方高度呈二次多项式正相关关系,Y向加速度与垂向填方高度未表现出明显的相关关系。
采用最小二乘法拟合后获取了X、Y向相对位移与垂向填方高度的关系函数:
(2)
(3)
式中:Hdx为X向相对位移(m);Sdy为Y向相对位移(g);x为垂向填方高度(m)。
X向加速度与垂向填方高度的关系函数:
(4)
式中:Ax为X向相加速度(m);x为垂向填方高度/厚(m)。
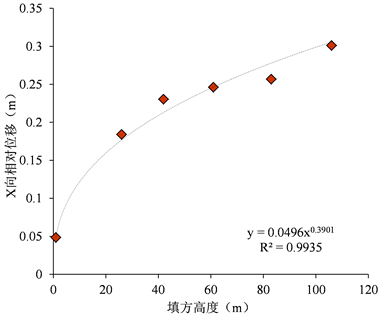
Figure 22. Relation curve between vertical fill height and X relative displacement
图22. 垂向填方高度与X相对位移关系曲线
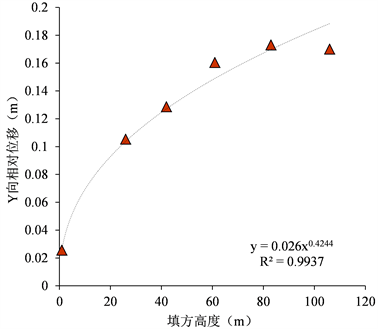
Figure 23. Relation curve between vertical fill height and Y relative displacement
图23. 垂向填方高度与Y相对位移关系曲线
坡顶4号监测点X向相对位移为填方体底部17号点的6.22倍,Y向相对位移为其6.64倍,X向加速度为其2.29,Y向加速度为其2.15倍。可见,垂向填方高度越高地震动响应越强烈,填方边坡垂向上存在较为明显的位移和加速度高程放大效应。
边坡坡面是震害相对集中的部位,选取坡面不同高程位置的4、5、6、7、8、9#监测点进行定量分析,监测点相对位移及加速度监测值,如表4。

Table 4. Data statistics of calculation results of ground motions on slope surface monitoring points
表4. 边坡表面监测点地震动计算成果数据统计
边坡坡面4、5、6、7、8、9#监测点监测数据反映出,X向相对位移与边坡高度呈线性正相关关系,如图24,Y向相对位移与边坡高度呈二次多项式关系,如图25。坡面加速度数据表现出“V”字型特征,即边坡上部和下部X、Y向加速度较大,中部加速度最小,如图26、图27。
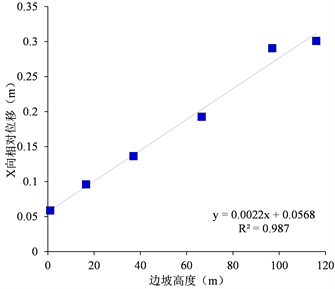
Figure 24. Relationship between slope height and relative displacement in X direction
图24. 边坡高度与X向相对位移关系曲线
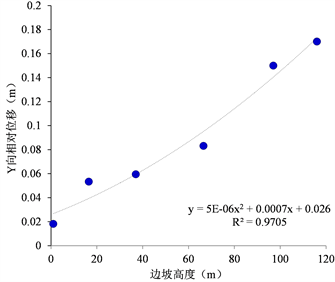
Figure 25. Relationship between slope height and relative displacement in Y direction
图25. 边坡高度与Y向相对位移关系曲线

Figure 26. Relationship between slope height and X-direction acceleration
图26. 边坡高度与X向加速度关系曲线
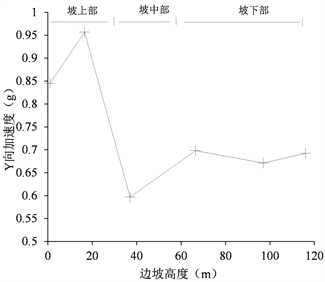
Figure 27. Relationship between slope height and Y-direction acceleration
图27. 边坡高度与Y向加速度关系曲线
采用最小二乘法拟合后获取了X、Y向相对位移与边坡高度的关系函数:
(5)
X向加速度与边坡高度的关系函数:
(6)
式中:Hfx为X向相对位移(m);Sfy为Y向相对位移(g);x为边坡高度(m)。
分析得出,坡面变形量坡顶部位最大,靠近坡脚部位最小,相对位移表现出明显的高程放大效应。加速度监测数据反映出,边坡上部1/3至顶部部位加速度变化最显著,其次为坡脚部位,边坡中部最弱,加速度与边坡高度表现出“V”字型特征关系。
4. 震后失稳机制与地下水工程效应
大量的工程实例及震害调查显示,很多时候,边坡在地震期间并不失稳,而是在震后很长一段时间才发生失稳,这类滑坡称之为后发型滑坡 [17]。后发型滑坡破坏的根本原因在于强震过程中,由于坡肩的端部效应,使得地震加速度在坡肩一定范围内产生弧形裂缝,这种裂缝虽然没有导致失稳破坏,但它导致了边坡稳定性下降。且由于震后边坡土石松动开裂,为雨水的入渗创造了条件,从而导致边坡内部地下水径流路径发生变化,降低边坡岩土体力学强度,加速地下水渗流潜蚀速度,经时间累积最后失稳。
同时地震作用将引发朝孔隙水压力效应,对边坡的稳定产生非常显著的影响,将加剧边坡的永久变形,威胁边坡的稳定。在上述地震动响应分析基础上获取了边坡竖向监测点地震作用下超孔隙水压力的时程变化关系曲线,如图28。
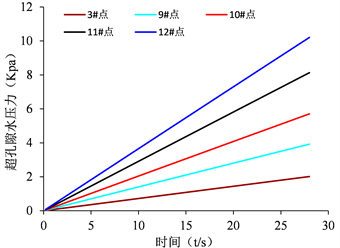
Figure 28. Variation curve of super-pore water pressure under earthquake
图28. 地震作用下超孔隙水压力变化曲线
图线反应出孔隙水压力随地震持时呈线性正相关关系,坡顶正下侧填方底面超孔隙水压力最大,超孔隙水压力值达11 Kpa,超孔隙水压力从填方体底部向上至坡顶呈逐步减小趋势。
5. 结论
1) 高地震烈度区高填方边坡地震动响应特征:① 边坡中上部地震动效应大于中下部地震动响应,坡面上部1/3至坡顶的地震动响应最剧烈;② 顶部表现出越靠近临空面地震动越强烈,向后缘延伸地震动响应逐步减弱;③ 坡体内部地震效应较弱,越靠近表面地震动响应越强烈,建设中应进行重点加强抗震设计和边坡加固工作。
2) 地基不均会产生地震波的差异性放大作用,导致坡体沉降、开裂、滑塌破坏,加剧震害。建议在填方过程中应对不均匀地基进行处理,特别是边坡部位,应重点处理以确保边坡的稳定。
3) 地震后边坡土石松动开裂,为雨水的入渗创造了条件,从而导致边坡内部地下水径流路径发生变化,降低岩土体力学强度,加速地下水渗流潜蚀,易造成震后失稳,震后应及时采取有效应的应急处置措施。
4) 地下水具有浸泡软化填方地基土,劣化岩土物理力学性能,渗流潜蚀破坏填筑体的工程效应,并且强震作用产生的高孔隙水压力和超孔隙水压力将进一步加剧边坡的变形、破坏。
NOTES
*通讯作者。