1. 引言
“电路基础理论”是高等学校电子信息类专业的一门重要的专业基础课程 [1]。其中,动态电路是非常重要的组成部分,同时也是一个教学难点。相较于电阻电路,集总动态电路的拓扑约束不变,而动态元件的伏安特性则由简单的比例关系变成了微积分关系;电路的数学模型也从代数方程变成了微分方程。电阻电路中各部分的电流、电压之间总是一个比例关系;而当动态电路的状态发生突变时,电路系统要经历一个过渡过程后再次进入稳定状态。“电路基础理论”引入正弦量的相量表示法来分析电路的正弦稳态响应;引入谐波分析(傅立叶级数)来分析非正弦周期电流电路的稳态响应。在动态响应方面,“电路基础理论”一般是用经典的数学方法分析一阶动态电路和二阶动态电路的零输入响应;引入单位冲激函数、系统单位冲激响应以及卷积积分等数学概念来描述动态电路在一般激励下的零状态响应。而拉氏变换和S域方法则通常在后续章节介绍。在许多相关专业的培养方案里,在“电路基础理论”之后还会有“信号与系统” [2]。“信号与系统”对信号和系统给出了更一般化的描述,信号的时域、频域与S域分解,系统的时域、频域与S域分析,依次展开,层层推进,概念丰富、逻辑清晰、理论完整,无疑在更高的层面上提供了分析包括电路系统在内的动态系统的理论方法。总之,“电路基础理论”以电路分析任务为导向;而“信号与系统”则偏重于分析方法的系统性。两门课程存在某些重复现象。
近年来,在一些高等学校的相关专业将“信号与系统”和“电路基础理论”两门课程合并为“电路、信号与系统”。为了寻求更加合理、高效的课程组织体系和教学方法,用更少的课堂学时资源让学生更好地掌握电路与信号系统的核心理论并能够灵活地应用于解决实际问题,笔者之前提出了“电路、信号与系统”课程的总体组织框架 [3],即,电路篇、信号篇和系统篇。基本思想是,在电路篇里,首先在电阻电路的部分里介绍电路所特有的基本规律、定理和分析方法;在动态电路部分介绍基本的动态元件(电感、电容等)的伏安关系,动态电路微分方程的列写以及响应的构成,强调动态电路的响应分为动态响应和稳态响应两个部分。在信号篇里,以线性叠加定理为切入点,系统介绍信号的时域、频域以及S域的分解。在强调积分、傅氏和拉氏三大变换的物理意义的同时为分析动态系统提供必要的数学工具。在系统篇里则将系统分析分为动态分析和稳态分析两个部分,灵活应用数学工具为系统分析服务。
“电路基础理论”和“信号与系统”两门课程的结合点在于动态电路的分析方法。如何在新的“电路、信号与系统”课程内容组织体系里具体实施动态电路的教学,是一个值得认真研究的问题。与电阻电路不同,动态电路对于激励信号的响应不是一个比例的、即时的关系,而是存在一个动态过程和稳态响应两个部分。笔者在关于相量与频域分析的文章中 [4],已经较为具体地讨论了动态电路稳态响应的教学方法,因此,本文将着重探讨动态电路动态过程的教学方法。
2. 动态电路教学任务与教学思路
动态电路对激励的响应分为过渡过程和稳态响应。过渡过程反映了动态电路在系统激励状态突变(换路)时,电路中电压或电流从原有的稳定状态到新的稳定状态的变化方式和快慢;而稳态响应则反映了电路在一个稳定的激励作用下,电压或电流的变化规律。动态电路教学任务在于让学生了解电路过渡过程和稳态响应的实际意义并熟练掌握相应的分析方法。具体的教学内容应包括:1) 理想电感、电容的伏安关系;2) 动态电路微分方程的列写;3) 动态电路响应的构成;4) 动态过程的一般分析方法,包括时域和S域方法;5) 稳态响应的一般分析方法,包括频域和相量分析方法;6) 一阶、二阶电路的动态过程和稳态响应。
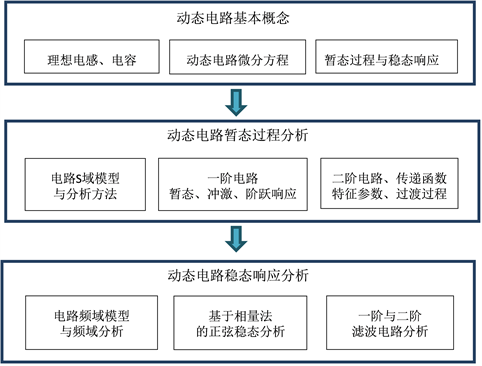
Figure 1. Teaching idea of dynamic circuit in the curriculum organization system of circuits signals and systems
图1. “电路、信号与系统”课程内容组织体系下动态电路的教学思路
图1给出了在新的“电路、信号与系统”课程内容组织体系下,动态电路的教学思路。首先在电路篇中介绍动态电路的基本概念,包括1) 理想电感、电容的伏安关系;2) 动态电路微分方程的列写;3)以一阶动态电路为例介绍响应的构成,说明暂态响应和稳态响应的物理意义。在系统篇的系统动态分析部分先介绍电路的S域模型和电路动态过程的一般分析方法,强调电阻电路的分析方法完全适用于电路的S域模型;接着具体分析一阶和二阶电路的暂态过程与电路特征量之间的关系。基本思想是把时域与S域打通,厘清数学知识、系统一般方法与电路特有理论三者之间的关系,在一个更加清晰,高效的教学体系里完成动态电路过渡过程分析的教学任务。最后在系统的稳态分析部分介绍电路的频域模型与相量分析方法。新的课程组织体系在介绍了一般系统频响特性、系统稳态响应与频响特性的关系基础上,先介绍电路的频域模型、电路稳态响应的频域分析方法,之后再介绍基于相量的电路正弦稳态分析。这样做有两个益处:一是大幅减少课堂授课学时;二是有利于学生深入理解频域分析与相量法正弦稳态分析的本质和内在联系,在实际分析电路问题时能够灵活地加以应用。关于动态电路稳态分析教学方法的详细讨论请参考文献 [4]。下面具体讨论动态电路动态过程的教学方法。
3. 动态电路动态过程的教学方法
3.1. 一阶电路动态过程的教学方法
一阶电路相对简单,采用微分方程的经典解法来分析也比较容易。然而,学生还是不易把握零输入响应和暂态响应之间的联系与区别,不易理解冲激响应和阶跃响应的本质,更有学生不自觉地陷入“三要素法”解题技巧的练习而忽视了对实际问题的宏观理解。
在新的“电路、信号与系统”课程内容组织体系里,由于在“信号篇”部分,从信号分解的角度切入,完整地解决了卷积积分、傅立叶变换以及拉氏变换等数学问题,所以在系统篇里可以没有数学障碍地讨论系统分析的基本概念和方法。在系统动态分析部分把时域和S域打通来讨论系统的动态响应,把系统冲激响应
和系统函数
直接联系起来,看清楚S域与时域特性的关系。在讨论电路的动态过程时,只要建立电路的S域模型便可以从系统的层面,方便地讨论电路的动态过程。
具体到一阶电路,首先给出一阶电路的几种基本形式,推演一阶电路传递函数的基本形式
和
,强调系统参数
与具体电路参数之间的关系。利用一阶电路的传递函数
依次分析它的冲激响应、阶跃响应以及有始周期信号激励下的暂态响应。可以得出结论,电路的暂态响应具有与其冲激响应相同的形式。因此,可以通过分析它的冲激响应或者其传递函数的极点分布来了解电路的过度过程。一阶电路的暂态过程具有指数衰减的形式,衰减的快慢则取决于电路的时间常数
。
3.2. 二阶电路动态过程的教学方法
首先从学生们比较熟悉的RLC串联电路入手,分别推导出在不同元件两端输出时的系统函数:
、
、
和
,其中,
、
。之后,给出若干其他形式的二阶电路,同样可以得到以上四种系统函数,只是阻
尼系数
、固有频率
与电路参数的关系与电路形式有关。建立了二阶电路系统模型,借鉴一阶电路动态分析得到的结论,即系统的极点分布决定了过度过程,便可以通过讨论二阶电路的极点分布来分析二阶电路的过渡过程。容易求得二阶电路的两个极点:
由此可知在二阶电路的暂态过程在过阻尼和临界阻尼两种情况下是指数衰减的,而在欠阻尼情况下是一个指数衰减的震荡过程,衰减的快慢取决于阻尼系数
,而震荡频率则同时与固有频率
和阻尼系数
有关。
至于系统函数
零点分布对系统特性的影响,可以通过讨论系统在正弦激励下的稳态响应部分,给学生一个初步的概念,为在系统稳态分析部分讨论滤波器做一个铺垫。
4. 结语
在“电路基础理论”课程里,相较于电阻电路,动态电路分析一直是一个教学难点。本文在新的“电路、信号与系统”课程内容组织里,具体讨论了动态电路分析,特别是动态电路暂态过程分析的教学方法。基本思想是,厘清数学工具、系统方法和电路知识三者之间的关系。在系统动态分析中,将时域与S域打通,避开繁杂的数学推演,集中讲清系统动态分析的基本概念和分析方法,然后应用于动态电路的分析。从动态电路的系统函数入手,讨论一阶、二阶电路参数与电路过渡过程的形式与快慢之间关系。教学实践表明,新的教学方法能够在显著减少课堂授课学时的同时,达到更好的教学效果。
参考文献