1. 引言
双曲方程作为偏微分方程中的一类重要方程,其解中往往出现间断,因此对于数值方法提出很大挑战。针对双曲守恒律方程,一系列的格式被提出和发展,例如Godunov格式 [1],Lax-Friedrichs格式 [2],总变差递减(Total Variation Diminishing, TVD) [3] [4],总变差有界(Total Variation Bounded, TVB) [5],加权本质无震荡格式(Weighted Essentially Non-Oscillatory, WENO) [6] 等。
间断有限体积元方法最早在2004年 [7] 中被YeXiu提出,作者将有限体积元方法与DG方法结合,针对椭圆问题提出了间断有限体积元方法。之后,毕春加将此方法推广到了抛物问题及双曲问题 [8] [9]。该方法不仅构造简单,还具备保持物理量间局部守恒、可以处理复杂边界、可并行计算等优点,发展前景广阔。在2009年,陈大伟等借鉴了控制体积有限元方法与龙格–库塔间断有限元方法,提出龙格-库塔控制体积间断有限元方法(Runge-Kutta Control Volume Discontinuous Finite Element Method, RKCVDFEM),保证了数值解的局部守恒性且可以很好的处理激波间断问题。但RKCVDFEM使用了minmod限制器,由于该限制器中参数M的选取依赖于不同的问题,从而限制了方法的适用范围。
区别于传统的间断有限体积元方法 [10] [11] [12] [13] [14],本文基于SSP Runge-Kutta时间离散方法,采用MPS (Maximum-principle-satisfying)的高阶精度限制器,构造了保极值间断有限体积元方法来求解双曲守恒律方程,并通过经典数值算例来验证方法的可行性与高效性。
2. 格式的构造
2.1. 空间离散
一维守恒律方程
这里的f是流通量函数。剖分定义域,令
为剖分节点,第i个单元记为
,单元长度为
。在每个控制单元
上依次选取3个插值节点,分别记为
,围绕插值节点选取控制体积,三个控制单元分别记为
,
,
,试探函数空间
选为线性元空间,相应的基函数选取为Lagrange基函数。选取的基函数记为
,则单元形状函数
为
选取检验函数为控制单元
上的分片常数函数,相应的基函数
从原方程出发进行空间离散。先在方程两边同时乘以检验函数v,并在一个单元
上做积分,u用
来代替
其中
,即
就是把
带入单元形状函数
中求得,而又由于
无定义,故本文采用Lax-Friedrichs数值流通量来定义
其中
。整理方程组得
,
,
当基函数取线性元与二次元分别对应的矩阵A如下
,
。
2.2. 斜率限制器
保极值的限制器
为了抑制数值振荡,引入MPS (Maximum-principle-satisfying)高阶精度限制器。
,
,
其中
,设
是区间
上的正交权重,可以令
。
在该限制器中
表示在
时刻单元上的数值解,其单元平均值
属于区间
,参考 [15] [16]。
Shu在 [17] 中证明了该限制器不会破坏高阶的精度。
2.3. 时间离散
半离散后得到常微分方程组,使用SSP Runge-Kutta格式 [18]
3. 算例
3.1. 算例1线性对流方程
计算讨论在周期边界条件下的该算例在相同时间下,基函数分别为线性元、二次元时,它们的误差与收敛阶。计算结果见表1和表2。
通过例子可以看出,对于
元,实际计算可以达到二阶精度,而对
元,计算可以达到三阶精度。
3.2. 算例2 Burgers方程
边界条件选取周期边界条件,在
时出现激波。由图1~2可知当
时结果没有激波出现,由图3~6可知当
和
时,结果出现激波。可以看到数值解在间断附近有良好的分辨率。

Figure 1.
,
图1. 剖分60份时的示意图,

Figure 2.
,
图2. 剖分100份时的示意图,
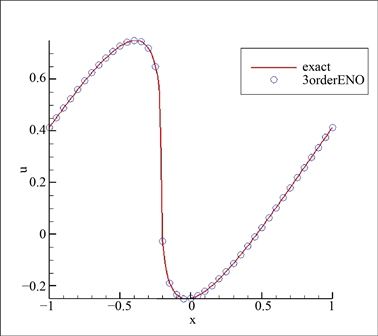
Figure 3.
,
图3. 剖分60份时的示意图,

Figure 4.
,
图4. 剖分100份时的示意图,
3.3. 算例3 Buckely-Leverett方程
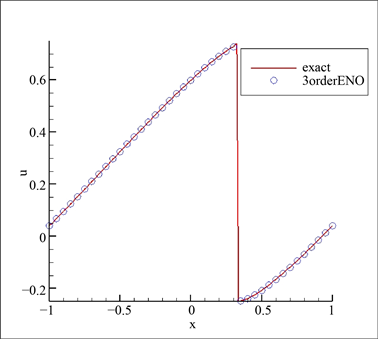
Figure 5.
,
图5. 剖分60份时的示意图,

Figure 6.
,
图6. 剖分100份时的示意图,
由图7~8可知,通过比较数值解与五阶WENO格式下的参考解可以发现,保极值间断有限体积元方法下的数值解在大梯度处无震荡,而且与参考解有完全类似地良好计算效果。
3.4. 算例4 交通流问题
考虑一段20 km长的公路,入口的密度是50 veh/km。(入口密度用单位长度路段内的车辆总数来表示)对于所给出的初值条件,我们考虑入口条件变化。在两个小时段分析,最初10分钟入口关闭,10分钟到30分钟,提高到入口密度75 veh/km,30分钟后入口密度恢复到50 veh/km。初值条件见图9。

Figure 7.
,
图7. 剖分40份时的示意图,

Figure 8.
,
图8. 剖分80份时的示意图,
计算结果见图10~13,在本算例中,分析了90分钟内因入口条件变化导致的交通流问题,通过将各个时间节点的车流密度变化图与该算例的准确解作对比,可以看出吻合情况较好。
4. 结论
本文研究了保极值的间断有限体积元方法,通过使用MPS的限制器使其保持高阶精度,守恒的同时又能满足极值原理。通过计算结果进行对比分析,证实了该保极值的间断有限体积元方法具有其理论设计的高精度和对间断高分辨率的特性。
基金
内蒙古大学科研发展基金(21100-5187133);内蒙古自治区人才开发基金项目(12000-1300020240)。

